回帰分析で考慮すべき事項
体系的な学習が進んでいないので、過不足や誤認等あるかもしれないが、回帰分析で考慮すべき問題に以下があるというのが現状認識。
- 多重共線性
- 交互作用
- オーバーフィッティング
正則化
多重共線性についてのアプローチが正則化であり、Lasso回帰等が正則化を含んだ回帰分析というのが現在の自分の認識。
glmnetは以前の記事に書いたとおり、クロスバリデーションの過程で最適なペナルティ $\lambda$ を決定しているが、参考記事をよく読んでみるとテストデータの予測や係数出力の際にはこの $\lambda$ を指定してあげなければ見つけた最適値を反映しない。
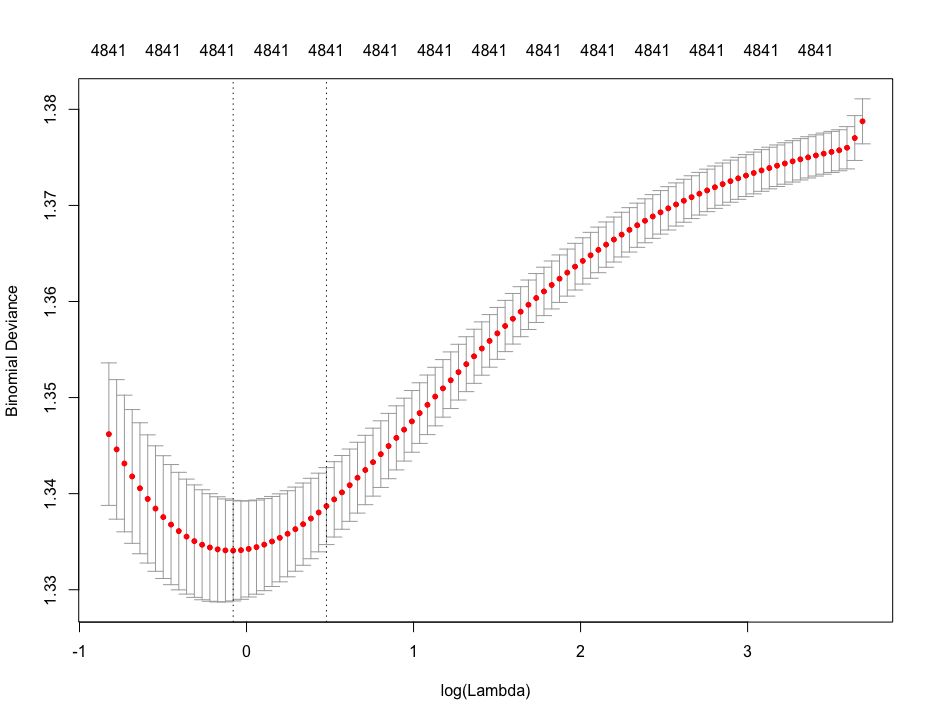
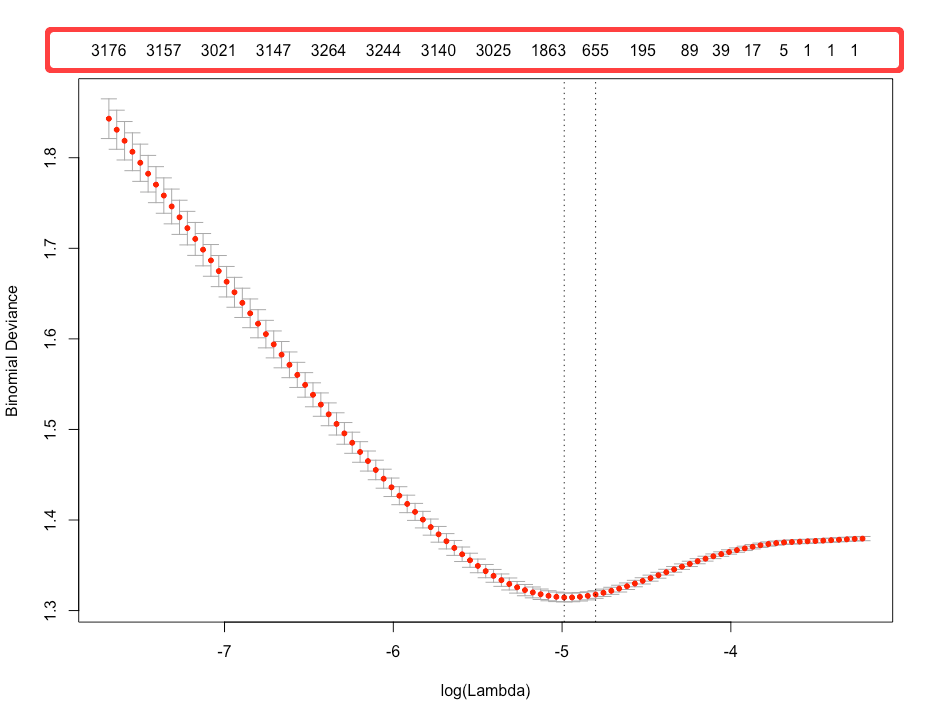
そしてその最適値は以下プロットの中に表現されている。(例示はRidge回帰の結果プロット)
グラフで表現されている赤点はモデルのMSE(誤差の総量の統計的な要約値=偏差平方和)であり、縦の点線が二本並んでいるうちの、左側が誤差が最小になる点、右側が最小点から1SE(標準偏差の1倍?)分の誤差を許容した点。
この $\lambda$ を反映させるには、予測や係数出力の際に s="lambda.min" などと引数を指定してやる必要がある。
> prd <- predict(lasso.cv, newx = tx, type = "class", s="lambda.min") # 最小値
> prd <- predict(lasso.cv, newx = tx, type = "class", s="lambda.1se") # 最小値から1SE
> coef(lasso.cv, s="lambda.min") # 最小値
> coef(lasso.cv, s="lambda.1se") # 最小値から1SE
誤差が少ないほうが単純に精度が良いということだが、1SEは何のためにプロットに表示されているかと考えると、おそらく最小値の $\lambda$ でオーバーフィッティングしてしまう場合の第二候補なのだと思われる。
また、Lasso回帰の場合は係数がゼロになる形で変数選択されるが、選択されて残っている変数の次元数がグラフ上部に横軸に沿って表示されている。
例示のような超多次元データセットを扱っている場合等は、これを指標にモデルの $\lambda$ を決定する場面もあるのかもしれない。