記事について
数理モデルとかを一切理解しないまま仕事でやったので、手順だけでも備忘録として残す。
全体のRスクリプトはこちら(lasso.r)
以下参考。
-
ロジットモデル
-
正則化について
概要
結果が二値をとる事象(CVする/CVしない、など)を予測する。
結果に起因すると思われる情報を説明変数として、実績を目的変数としてRのglmnetで回帰モデルを作成する。
ラッソ回帰でなくても大体以下の流れを汲むのかなという認識。
-
説明変数と目的変数のサンプルデータを学習用データと、テスト用データに分ける
学習8割、テスト2割が一般的?
このとき、学習データの正例と負例のバランスに注意する。
(サイトのCVユーザーと未CVユーザーなどの場合、CVユーザーが圧倒的に少なくなっていたりすると例数の多い方に学習パラメータが傾いてしまう) -
学習データを使って学習する
過学習による汎化性能の低下を気にする必要がある。
過学習(over-fitting)というのは、学習結果のモデルが外れ値のようなものまで拾いにいってしまうほど複雑化してしまった状態?という認識。
汎化性能の低いモデルはデータセットによって予測精度が大幅に変わってしまい安定しない。 -
テストデータによる精度検証
テスト用に分けておいたデータを用いて予測値と実績値の誤差を見る。 -
予測モデルの定式化
学習によって得られた偏回帰係数(説明変数ごとの重み)から予測の為の計算式を作る。
学習?
そのままglmnetに通す。
lasso.net <- glmnet(mx, my, family = "binomial", alpha = 1)
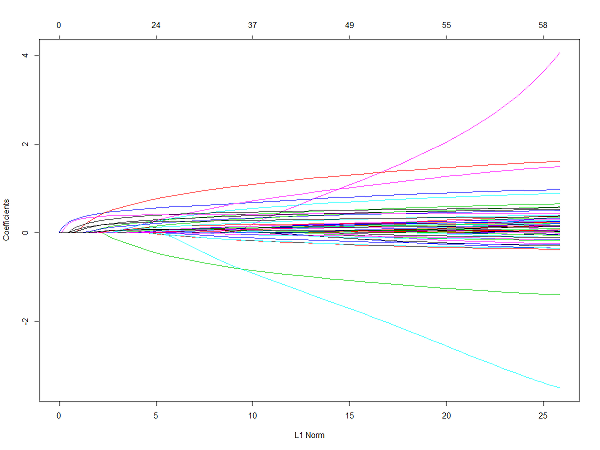
plot(lasso.net)
なるほど、わからん。
横軸の一番左が正則化ペナルティが最大の状態で、ペナルティが弱まるほどグラフが外に広がっている。
グラフの一本一本は各説明変数の寄与度のようなもので、後述する偏回帰係数がそのまま出ている?
ここから何を読み取るのか?という意味で一行目。
学習(cross validation)
交差検定を伴う学習。
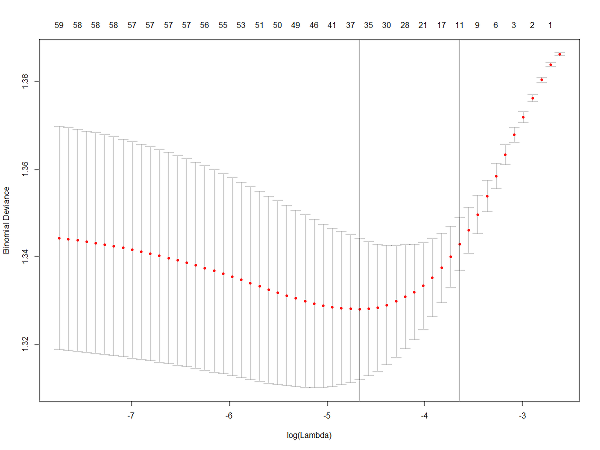
~~過学習による汎化性能の低下を防いでいるという認識。~~最適な$\lambda$(ペナルティ強度)を決定している?らしい。
lasso.cv <- cv.glmnet(mx, my, family = "binomial", alpha = 1)
plot(lasso.cv)
引数のalphaに渡す値によってLasso回帰、Ridge回帰、Elastic Netとして扱われ方が変わる。($0 \leqq \alpha \leqq 1$)
これらは正則化という処理においてL1正則化(Lasso)、L2正則化(Ridge)に当たるものらしい。汎化性能を担保するアプローチがなんか違うっぽい?
familyに"multinomial"を指定すると多クラス分類(3つ以上の分類)ができる。
予測と正答率
混同行列(confusion-matrix)で正答率を確認する。
> prd <- predict(lasso.cv, newx = tx, type = "response")
> border = median(prd)
> table(ty, floor(prd + (1.0 - border)))
ty 0 1
0 2261 2231
1 58 212
このとき、正例と負例に大きな偏りがあるとサンプルサイズの大きい方に予測が偏ることで正答率が高く見えてしまうが、予測精度の評価として単純にそれでいいのかという疑問がある。
不均衡問題についての言及ではないが以下参考。
-
Amazon Machine Learningの評価指標まとめ
再現率と適合率の調和平均をとるF1値というのが良い?
偏回帰係数
学習によって得られたパラメータを出力する。
> coef(lasso.cv)
72 x 1 sparse Matrix of class "dgCMatrix"
1
(Intercept) -0.29268660
x01 .
x02 .
x03 .
x04 .
x05 .
x06 .
x07 .
x08 .
x09 .
x10 .
x11 .
x12 .
x13 .
x14 .
x15 .
x16 .
x17 .
x18 .
x19 .
x20 .
x21 .
x22 .
x23 .
x24 .
x25 .
x26 .
x27 .
x28 .
x29 .
x30 .
x31 .
x32 .
x33 .
x34 .
x35 .
x36 0.44654091
x37 .
x38 .
x39 .
x40 0.42874766
x41 0.10780059
x42 0.09534120
x43 .
x44 .
x45 0.18472410
x46 .
x47 .
x48 .
x49 .
x50 .
x51 0.03912708
x52 0.01984098
x53 .
x54 .
x55 .
x56 .
x57 0.28637276
x58 .
x59 .
x60 .
x61 .
x62 0.37189459
x63 0.18172629
x64 .
x65 .
x66 .
x67 .
x68 .
x69 .
x70 .
x71 0.04421396
予測モデルの式
ロジットモデルの回帰式?がこれらしい。
y = \frac{1}{1 + e^{-1 ( \alpha + \beta_{1} x_{1} + \beta_{2} x_{2}+ \beta_{3} x_{3} \cdots \beta_{n} x_{n})}}
文字の意味は以下。
- $n$ : 説明変数の数
- $y$ : 予測する事象の生起確率($0 \leqq y \leqq 1$)
- $x_{n}$ : 説明変数 ($0/1$)
- $\alpha$ : 切片(定数)
- $\beta_{n}$ : 各説明変数に対する偏回帰係数(定数)
- $e$ : 自然数(定数)
なので先述の出力内容について、$\alpha$に(Intercept)を、$\beta_{n}$には各変数の出力値を当てはめて以下となる。
(ドットが出力されている変数はL1正則化による変数選択で残らなかったものなので、項そのものを無くしてよい)
y = \frac{1}{1 + e^{-1 ( -0.292 + 0.446x_{36} + 0.428 x_{40} \cdots 0.044 x_{71})}}
これに予測したいサンプルが持つ説明変数$x_{n}$に値を代入して導出される$y$が予測確率になる。