背景・目的

サイト改善などで一般に用いられるABテストにおいて、2群の反応率(CVRなど)の差の有無をχ2乗検定などの統計的仮説検定で判断する場合、サンプルサイズが十分でないとタイプ2エラーになり、誤った評価をする可能性がある
- 詳しくは、以前の記事(Power Analysisとサンプルサイズの決め方)に記載している
そのため、ABテストを正しく行うにためは差があった場合に正しく検出できるだけのサンプルサイズを確保する必要がある
しかし、実際にはサンプルを集めるのにコストがかかる/サービス規模の都合上、サンプルが集まりづらい、などの自乗で十分なサンプルサイズがない場合も多い
また、χ2二乗検定では、有意差の有無しかわからず、差異の程度やどれくらいの確率で差があるか等がわからないという欠点もある
上記の2点を克服する方法としては、ベイズ統計学の枠組みで比率の差を扱う「ベイズABテスト」が有効だと思われる
- 具体的には、ベイズABテストでは「どれくらいの差がある確率が◯%」というように差の度合いまで評価できる
- また、差がある確率まで評価できるため、サンプルサイズが小さくても、「どれくらいの確信を持って差がある/ない」と評価でき、差の有無を01で判断してしまわないため、タイプ2エラーにならずに済むと思われる

上記の経緯でベイズABテストに興味を持ったので、今回はベイズABテストについて調べた内容をまとめました。

ベイズの公式の導出

ベイズの定理は有名なので書くまでもないかもしれませんが、自分の備忘も兼ねて以下に記載しておきます。高校数学で習う同時確率と条件付き確率の関係式を変形することでベイズの定理が導けます。

\begin{align}
P(A\cap B)&=P(A|B)P(B) \;-①\\
P(A\cap B)&=P(B|A)P(A) \;-②\\
P(A|B)P(B)&=P(B|A)P(A) \;\quad(①=②より)\\
P(A|B)&=\frac{P(B|A)P(A)}{P(B)} \;-③
\end{align}

上記の③式がベイズの公式です。$P(A)$を事前確率、$P(A|B)$を事後確率と呼んだりします。

χ二乗検定の代替としてのベイズABテストでは、得られたデータ($\boldsymbol{x}$)をもとに、反応率などのパラメータ($\boldsymbol{\theta }$)を推定することになるので、③式で用いている確率の表記を確率密度関数($f(\boldsymbol{x})$)の表記に変更し、$A$→$\boldsymbol{\theta }$、$B$→$\boldsymbol{x}$に置き換えた以下の式を使います。

\begin{align}
f(\boldsymbol{\theta }|\boldsymbol{x})&=\frac{f(\boldsymbol{x}|\boldsymbol{\theta } )f(\boldsymbol{\theta } )}{f(\boldsymbol{x})}\\
&=\frac{f(\boldsymbol{x}|\boldsymbol{\theta } )f(\boldsymbol{\theta } )}{\int f(\boldsymbol{x}|\boldsymbol{\theta } )f(\boldsymbol{\theta })d\boldsymbol{\theta }}\quad-④\\
&\propto f(\boldsymbol{x}|\boldsymbol{\theta } )f(\boldsymbol{\theta })\quad-⑤
\end{align}

上の式の各項の意味を簡単に記載しておきます。

$f(\boldsymbol{\theta }|\boldsymbol{x})$：事後分布
- 観察データによって更新された後の母数(パラメータとも言う)の分布
$f(\boldsymbol{x}|\boldsymbol{\theta } )$：尤度
- データ($\boldsymbol{x}$)を固定して(定数として扱い)、母数($\boldsymbol{\theta }$)を変数として扱った場合の確率密度関数のこと
- 尤度は事象の起こりやすさを表すが、確率と違って値が1を超えることもある
- 得られたデータの元で$\boldsymbol{\theta }$を変えていった時に、尤度が最大になる$\boldsymbol{\theta }$は「$\boldsymbol{\theta }$の値がその値である可能性が最も高い」ということ
$f(\boldsymbol{\theta })$：事前分布
- 事前の情報がない状態(データを観察する前段階)において、パラメータが従う(と想定される)分布
- データが得られる前にわかっている情報がない場合には「無情報事前分布」として、一様分布がよく用いられる
- 一様分布は$f(\theta)=1$で表され、母数$\theta$にどの値を入れても1となる
$f(\boldsymbol{x})$：正規化定数
- ベイズの公式の分子の部分
- 変数である$\boldsymbol{\theta }$を含まず、その名の通り定数
$f(\boldsymbol{x}|\boldsymbol{\theta } )f(\boldsymbol{\theta })$：カーネル
- ベイズの公式から分母を除いた、事前分布と尤度の積の部分(⑤式)
- ベイズの公式の分母は定数であり事後分布はカーネルに比例するので、事後分布の本質的な情報を含んだ部分と言える

ABテストの問題設定

ECサイト上でABテストを行う場面を想定し、2種類のクリエイティブ(1、2)が表示されたユーザ数と、コンバージョンユーザ数をそれぞれ以下の通りとします。単純にCVRを計算すると、1、2のCVRはそれぞれ$1.0$%、$2.2$%です。

クリエイティブ	CVあり	CVなし	TOTAL
1	10	990	1000
2	33	1467	1500

ここで、クリエイティブ1のCVユーザ数$x_{1}$は$n_{1}=10$、母比率$p_{1}$の二項分布に従い、クリエイティブ2のCVユーザ数$x_{2}$は$n_{2}=33$、母比率$p_{2}$の二項分布に従うとします。

クリエイティブ1と2とでCVRは互いに独立なので、
データ：$\boldsymbol{x}=(x_{1}, x_{2})=(10, 33)$
母数：$\boldsymbol{\theta }=(\theta_{1}, \theta_{2})=(p_{1}, p_{2})$
より、
尤度：$f(\boldsymbol{x}|\boldsymbol{\theta })=f(x_{1},x_{2}|p_{1},p_{2})=f(x_{1}|p_{2})\times f(x_{1}|p_{2})$
また、事前分布 $f(\boldsymbol{\theta})$を一様分布 ( $f(\boldsymbol{\theta})=1$ )とすると、事後分布は

\begin{align}
f(\boldsymbol{\theta }|\boldsymbol{x})&\propto f(\boldsymbol{x}|\boldsymbol{\theta } )f(\boldsymbol{\theta } )\\
&=f(\boldsymbol{x}|\boldsymbol{\theta})\quad(\because f(\boldsymbol{\theta})=1)\\
&=f(x_{1},x_{2}|p_{1},p_{2})\\
&=f(x_{1}|p_{1})\times f(x_{2}|p_{2})\\
&={}_{1000} \mathrm{C} _{10} p_{1}^{10}(1-p_{1})^{990}\times{}_{1500} \mathrm{C} _{33} p_{2}^{33}(1-p_{2})^{1467}
\end{align}

となります。

Rでの簡易シミュレーション

実際に上記の式を描画してみたいですが、確率密度関数として描画するには④式に出てくる分子の積分計算も必要であり、うまく描画できそうになかったため、ひとまずシミュレーションによって擬似的に描画してみます。

データが与えられた元で(データは定数として動かさずに固定して)、パラメータを事前分布に従う形で変数として動かし、上記の事後分布の式に代入した際に返却される値をplotしていくことで、"事後分布の確率密度関数のような散布図"を描いてみます。

library(tidyverse)

# 正例数とサンプルサイズの設定
x1 <- 10; n1 <- 1000; x1/n1
x2 <- 33; n2 <- 1500; x2/n2

choose(n1, x1) # 組み合わせの計算
choose(n2, x2)

# カーネル
post <- function(p1, p2) {
  res <- choose(n1, x1)*p1**x1*(1-p1)**(n1-x1) * choose(n2, x2)*p2**x2*(1-p2)**(n2-x2)
  return(res)
}

# データが与えられた元で(データは定数として動かさずに)、
# パラメータを事前分布に従う形で、変数として動かす
# P1、p2を変数として変化させていく
p1_value <- seq(0, 0.05, length=100) # 0から0.5までを100等分
# p1_value <- runif(1000, min=0, max=0.5) # 乱数を発生させる場合
p2_value <- seq(0, 0.05, length=100)
# p2_value <- runif(1000, min=0, max=0.5)

p1_l <- '' # 母数1の格納先
p2_l <- '' # 母数2の格納先
lf_l <- '' # 尤度の格納先

# p1とp2をそれぞれ変化させ、
# 事後分布を導出する式に代入することで、事後分布を得る
system.time(
  for (i in p1_value) {
    for (j in p2_value) {
      p1_l <- append(p1_l, i)
      p2_l <- append(p2_l, j)
      lf_l <- append(lf_l, post(i, j))
    }
  }
)

# 最初の値は空白なので除外する
p1_l <- p1_l[2:length(p1_l)]
p2_l <- p2_l[2:length(p2_l)]
lf_l <- lf_l[2:length(lf_l)]

p1_l <- as.numeric(p1_l)
p2_l <- as.numeric(p2_l)
lf_l <- as.numeric(lf_l)

res <- data.frame(p1=p1_l, p2=p2_l, lf=lf_l)
res2 <- res %>% 
  tidyr::gather('param', 'value', p1, p2)

# P1、p2の確率密度(のような散布図)の描画
ggplot(data = res2, aes(x=value, y=lf, color=param)) + 
  theme_bw() + 
  geom_point(size=1, alpha=.8)

# グラフを分けて描く場合
# ggplot(data = res2, aes(x=value, y=lf)) + 
#   theme_bw() + 
#   geom_point(size=0.1) + 
#   facet_wrap(param~.)

# P2を大きく5つにカテゴライズする
categoryData <- cut(res$p2, breaks = 5, right = FALSE)
plot(categoryData) # カテゴリごとのデータ数が均等になっているか確認
res$p2_cat <- categoryData

# P2を色分けした上でp1をplotする
ggplot(data = res, aes(x=p1, y=lf, color=p2_cat)) + 
  theme_bw() + 
  geom_point(alpha=.5) +
  geom_jitter()

事後分布導出の公式に当てはめ、$p_{1}$と$p_{2}$をそれぞれplotした結果が以下です。

$p_{1}$、$p_{2}$はそれぞれ0.01、0.02の付近で値が大きくなっており、ABテスト結果のデータを使って$p_{1}$、$p_{2}$を推定した結果として、妥当な値が出ているようです。

次に、ベイズの公式に$p_{1}$、$p_{2}$を当てはめた際に、$p_{1}$と$p_{2}$の関係性($p_{1}$がどの値をとっているときに$p_{2}$がどの値をとっているか)を簡易的に確認してみた結果が以下です。
$p_{2}$をカテゴリ化して色分けした上で、$p_{1}$の確率密度関数(もどき)をplotしています。

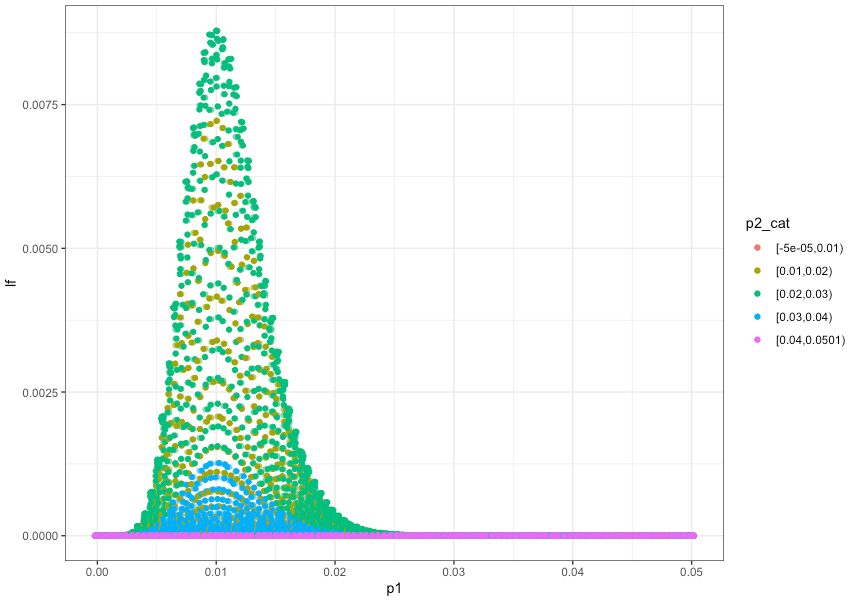
紫→青→黄緑→緑の順で山が高くなっていることがわかります。緑は$p_{2}$の値が0.02付近をとる時であり、$p_{2}$の尤度が高くなる場合です。ベイズの公式から自明ではありますが、$p_{1}$と$p_{2}$の両方の尤度が高いときに事後分布の値(図では縦軸の値)も大きくなる、ということがわかります。

MCMC法により、ベイズABテストを実践

MCMCで事後分布に従う乱数を得て、それらを集約することでABテストに用いたクリエイティブ(1，2)のCVRに差があるのかどうかの評価を試みます。MCMCの実行にはstanを用います。

以下が今回利用したstanのスクリプトです。

//bayesAB.stan
//ABテスト
data { 
  int<lower=0> x[2]; //正反応数 
  int<lower=0> n[2]; //データ数 
}
parameters {
  real<lower=0,upper=1> p[2]; //母比率
}
transformed parameters {
}
model {
for (i in 1:2) {
  x[i] ~ binomial(n[i],p[i]); // 文字コード都合で、チルダを書き直さないとうまく回らないことがあるので注意
  }
}
generated quantities{
  int<lower=0> xaste[2];
  real p_sa;
  real p_hi;
  real Odds_hi;
  real Odds[2];
  p_sa = p[1]-p[2]; // 比率の差
  p_hi = p[1]/p[2]; // 比率の比
  Odds[1] = p[1]/(1-p[1]); // p1のオッズ
  Odds[2] = p[2]/(1-p[2]); // p2のオッズ
  Odds_hi = Odds[1]/Odds[2]; // オッズ比(正反応は他方の反応の何倍生じやすいか)
  for (i in 1:2) {
    xaste[i] = binomial_rng(n[i], p[i]); //事後予測分布
}
}

stanファイルのgenerated quantitiesブロックではdataブロック、parametersブロック、transformed parametersブロックで宣言されたパラメータや定数から、関数などを用いて新たにサンプリングする変数を設定できます。なお、generated quantitiesブロック内では「~分布名( )」を使用できず、ある分布に従う乱数を発生させる場合には「=分布名_rng( )」を使います。

今回、generated quantitiesブロックではサンプリングする変数として以下の内容を追加しています。

母比率の差分(CVRの差分)：$p_{1}-p_{2}$
母比率の比：$p_{1}/p_{2}$
$p_{1}$のオッズ：$p_{1}/(1-p_{1})$
$p_{2}$のオッズ：$p_{2}/(1-p_{2})$
オッズ比：$\frac{p_{1}/(1-p_{1})}{p_{2}/(1-p_{2})}$
事後予測分布：${\boldsymbol {x^{\ast }}}^{(t)}\sim f(\boldsymbol{\theta }^{(t)})\quad(t=1,...,T)$
- (TはMCMCにより得られた有効なサンプルサイズであり、$T=($イテレーション数 - バーンイン期間)✕chain数で求められる)
- 観測されたデータ$\boldsymbol x$ を所与のものとして固定し、母数$\boldsymbol \theta$ を事後分布に従って確率的に変動させた場合に生成される未来の観測値$\boldsymbol {x^{\ast }}$の分布のこと
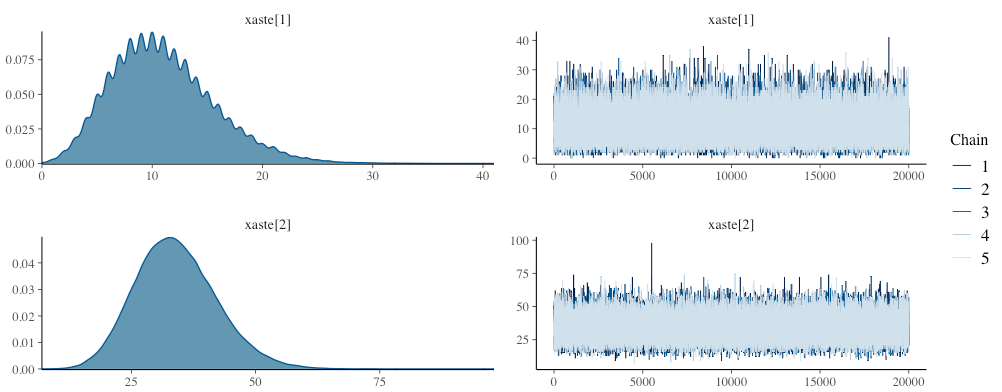
- 今回は母数が従う分布が二項分布なので、$x^{\ast }\sim Binomial(n_{i}, p_{i}) \quad (i=1,2)$

上記のstanスクリプトを、以下のRスクリプトから読み込んでMCMCサンプリングを行います。

# ベイズABテスト
# 2*2のクロス集計表の推測
library(tidyverse)


# Stanでのサンプリング ------------------------------------------------------------
library(rstan)
rstan_options(auto_write=T)
options(mc.cores=parallel::detectCores())

# ABテストのCV数(x1, x2)とサンプルサイズ(n1, n2)
x <- c(10,33); n <- c(1000,1500)

dat <- list(x=x,n=n)
scr <- "bayesAB.stan" # 先程のStanスクリプトを読み込む
prob <- c(0.025, 0.05, 0.5, 0.95, 0.975)
see <- 1234
cha <- 5 # chain数
war <- 1000 # バーンイン期間
ite <- 21000 # 乱数生成の繰り返し数
fi <- NA
print(ite-war) # 1つのchainごとに存在するMCMCサンプルの数

# MCMC
fit<-stan(file=scr,data=dat,
          seed=see,chains=cha,warmup=war,iter=ite, fit=fi)


# サンプリング結果の確認 -------------------------------------------------------------
# Stanオブジェクトからパラメータを取り出す
ext<-extract(fit, permuted=FALSE); # permuted=FALSE でMCMCサンプルの並び順が保持される

class(ext)
# [1] "array"

# 次元数。繰り返し数*chain数*パラメータ数で3次元のarrayになっている
dim(ext)

# 名称
dimnames(ext)
# $iterations
# NULL
# 
# $chains
# [1] "chain:1" "chain:2" "chain:3" "chain:4" "chain:5"
# 
# $parameters
# [1] "p[1]"     "p[2]"     "xaste[1]" "xaste[2]" "p_sa"     "p_hi"     "Odds_hi"  "Odds[1]"  "Odds[2]" 
# [10] "lp__"    
# parametersの名前はstanのparametersブロック & generated quantitiesで宣言された名前が使われる

# パラメタp1の1個目のchainのサンプルを100件取り出す
ext[, 'chain:1', 'p[1]'][1:100]
# ext[データ番号, chain名, パラメタ名]で各chain各パラメタの任意のサンプルにアクセスできる

# 結果の出力
print(fit, probs = prob)


# トレースプロットの描画 -------------------------------------------------------------
library(ggfortify)

# MCMCサンプルをchain別で時系列で並べてplotするとトレースプロットになる
autoplot(ts(ext[,,'p[1]']), 
         facets=F, # 5つのchainをまとめて1つのグラフにする
         ylab='p[1]', 
         main='trace plot')


# 事後分布の可視化 ----------------------------------------------------------------
# MCMCサンプルの各chainを合算してカーネル密度推定するとパラメータの事後分布のグラフになる
# ggplotで描画する場合
p1_df <- data.frame(p_1 = as.vector(ext[, , 'p[1]']))
ggplot(data = p1_df, aes(x = p_1)) + 
  geom_density()

# bayesplotで可視化するとデータ加工の手間が省けるため便利
library(bayesplot)

# p1, p2のMCMCサンプルのヒストグラム
mcmc_hist(ext, pars=c('p[1]', 'p[2]', 'p_sa', 'p_hi', 'xaste[1]', 'xaste[2]'))

# カーネル密度推定
mcmc_dens(ext, pars=c('p[1]', 'p[2]', 'p_sa', 'p_hi', 'xaste[1]', 'xaste[2]'))

# trace plot
mcmc_trace(ext, pars=c('p[1]', 'p[2]', 'p_sa', 'p_hi', 'xaste[1]', 'xaste[2]'))

# 事後分布とトレースプロット
mcmc_combo(ext, pars=c('p[1]', 'p[2]', 'p_sa', 'p_hi', 'xaste[1]', 'xaste[2]'))

サンプリング結果

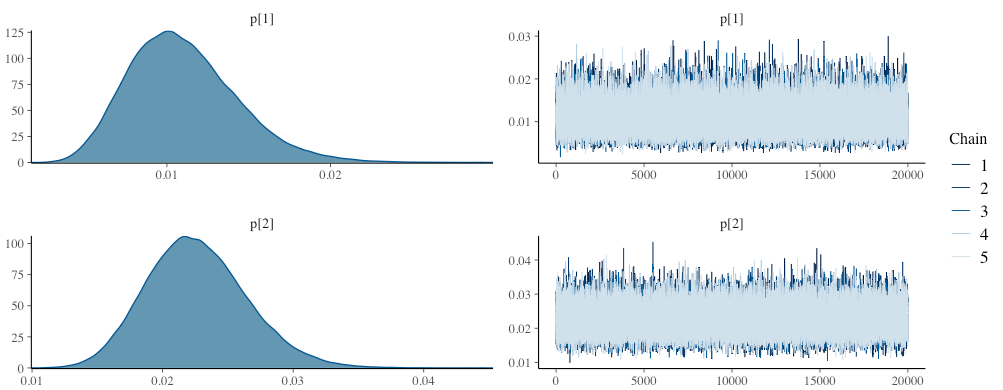
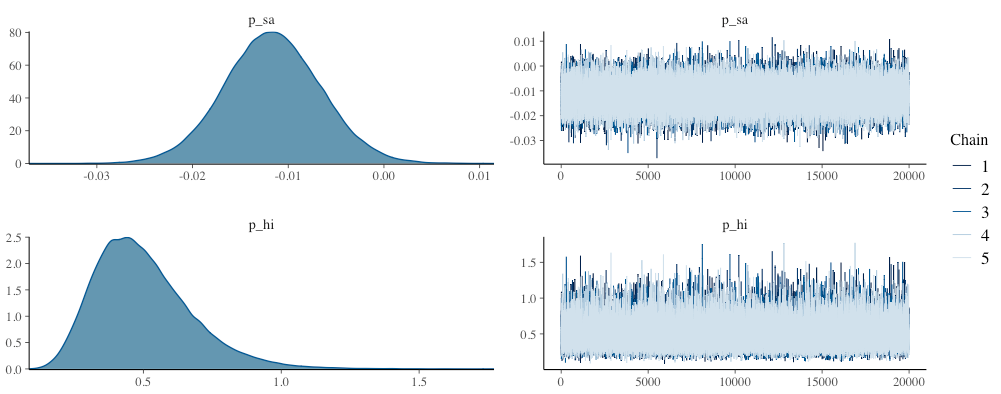
上記スクリプトを実行してMCMCサンプルを抽出した結果が以下です。パラメータ$p$の事後期待値(事後分布の平均値)はそれぞれ$p_{1}=0.01$、$p_{2}=0.02$で、単純にCVRを計算した場合とほぼ同じ値になりました。また、母比率の差分(真のCVRの差分。$p_{1}-p_{2}$)の事後期待値は$-0.01$であり、$p_{1}$は$p_{2}$に比べ$0.01$小さい可能性が示唆されました。

> # 結果の出力
> print(fit, probs = prob)
Inference for Stan model: bayesAB.
5 chains, each with iter=21000; warmup=1000; thin=1; 
post-warmup draws per chain=20000, total post-warmup draws=1e+05.

            mean se_mean   sd    2.5%      5%     50%     95%   97.5% n_eff Rhat
p[1]        0.01    0.00 0.00    0.01    0.01    0.01    0.02    0.02 90429    1
p[2]        0.02    0.00 0.00    0.02    0.02    0.02    0.03    0.03 90052    1
xaste[1]   10.99    0.02 4.67    3.00    4.00   11.00   19.00   21.00 95371    1
xaste[2]   33.99    0.03 8.14   19.00   21.00   33.00   48.00   51.00 94237    1
p_sa       -0.01    0.00 0.01   -0.02   -0.02   -0.01    0.00    0.00 90279    1
p_hi        0.50    0.00 0.18    0.23    0.26    0.47    0.82    0.91 87045    1
Odds_hi     0.49    0.00 0.18    0.22    0.26    0.47    0.82    0.91 86946    1
Odds[1]     0.01    0.00 0.00    0.01    0.01    0.01    0.02    0.02 90420    1
Odds[2]     0.02    0.00 0.00    0.02    0.02    0.02    0.03    0.03 90040    1
lp__     -223.99    0.00 1.01 -226.72 -226.01 -223.68 -223.03 -223.01 42386    1

Samples were drawn using NUTS(diag_e) at Fri Mar 12 23:37:57 2021.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

事後分布とtrace plot

MCMCによるサンプリング結果をカーネル密度推定すると事後分布に、時系列でplotするとtrace plotになります。下記は、MCMCによるサンプリング結果について、事後分布とtrace plotを描いたものです。

$p_{1}$、$p_{2}$については、Rでベイズの公式に当てはめて事後分布(を模した散布図)を描いた時と似た形状の分布ができています。また、先程確認した通り、それぞれ$0.01$と$0.02$の周辺で確率密度が高くなっています。

変数p_saは母比率の差分($p_{1}-p_{2}$)を表していますが、分布が原点の左側に位置していることから、$p_{1}$より$p_{2}$のほうが大きいことが伺えます。

ベイズABテストの結果

クリエイティブ1、2に差があるのか？どの程度の差がある確率がどれくらいなのか？を計算した結果が以下です。
差がある($p_{1}<p_{2}$である)確率は$99$%で、$0.01$以上の差がある確率は$63$%という結果になりました。

# p1<p2である確率 --------------------------------------------------------------
p_sa <- as.vector(ext[, , 'p_sa'])
round(mean(p_sa < 0), 2)
# [1] 0.99


# p1とp2の差が1％以上である確率 -------------------------------------------------------
p_sa <- as.vector(ext[, , 'p_sa'])
round(mean(p_sa <= -0.01), 2)
# [1] 0.63

終わりに

ベイズABテストでは、MCMCサンプルを使って「差がある確率」「◯◯%ポイントの差がある確率」が自由に計算できる点が便利だと感じました。一方で、自由度が高い分、Rやstanで記載するコード量がやや多くなるのは手間でもあります。手間を解消するなら、RのベイスABテスト用パッケージ{bayesAB}を使ってみたり、WEB上のツール(例えば、BAYESIAN A/B TESTING CALCULATOR)を、適宜利用してみると良いのかもしれません。

ちなみにですが、今回の問題設定ではχ二乗検定を行っても有意水準5%で有意差がつきます。(本当はχ二乗検定で差がつかない場合にベイズABテストでどうなるか見ようと思っていたのですが、適当にABテストの数値設定をしたためにχ二乗検定でも差がつく問題になっていました。おそらく、χ二乗検定で差がつかないようなケースでは、ベイズABテストでは差がある可能性が下がるのだと思われますが。)

# カイ2乗検定をした場合 --------------------------------------------------------------
dat <- matrix(c(10, 33, 990, 1467), ncol = 2)
# カイ2乗検定
res <- chisq.test(dat, correct=F) # correct=Fはイェーツの補正をしないという意味
# Pearson's Chi-squared test
# 
# data:  dat
# X-squared = 5.1112, df = 1, p-value = 0.02377

なお、今回記事を書くにあたり、教科書やWEBページを参照しつつまとめましたが、自己流な部分もあるのでもし間違いなどあればご指摘いただけると幸いです。

RとStanでBayes A/Bテスト