LoginSignup
3
3

More than 3 years have passed since last update.

@perico_v1

Power Analysisとサンプルサイズの決め方

Last updated at Posted at 2021-01-31

はじめに

Power analysis(検定力分析)とは統計的仮説検定において、対立仮説が真である場合に正しく検出できる(有意水準$\alpha $の元で正しく帰無仮説を棄却する)確率を評価することです。

比率の差の検定や独立性検定を行う場合、
- サンプルサイズが小さすぎると2群に差があったとしても正しく検出できない
- サンプルサイズが大きくても反応率の差分が小さすぎると正しく検出できない
ということが起こります。
ABテストの結果有意差がつかなかったから差がなさそう、と思う前に「そもそもサンプルが小さくないか」「反応率差が低すぎないか」も考慮する必要があります。

WebサービスなどでABテストを行ってユーザの反応を見る場合、どれだけサンプルが集まったら打ち切ればよいのか、テストの前に事前に目安を立てておきたいものです。

以下は、ABテストにおける、検定力分析を用いたサンプルサイズの決め方について調べた内容をまとめたものです。

問題設定と記号の説明

例として、2種類の薬剤AとBを2つのグループ(人数をそれぞれ$n_1$, $n_2$とし、人数比は$n_1:n_2=1:k$であるとします。)のグループに投与した場合を考えます。$n_1$, $n_2$のうち薬剤の効果が認められた人数をそれぞれ$m_1$, $m_2$とすると、薬剤の効果があった人数の割合はそれぞれ $p_1= \frac{m_1}{n_1}$, $p_2= \frac{m_2}{n_2}$と表せます。

ここで、帰無仮説 $H_0: p_1=p_2$, 対立仮説 $H_1: p_1<p_2$として、$p_1$, $p_2$の差を有意水準$\alpha $で検定する場合に、「$H_1$が真であったときに差を正しく検出できる確率 (検出力:$1-\beta $**) が◯◯%であるにはどれくらいのサンプルサイズが必要なのかを知りたい」、というのが問いです。

式の導出

独立な2群の比率差の検定に用いる式から、検出力を考慮した場合の必要サンプルサイズを求めます。$H_0$のもとでの両群の母集団比率の推定値を以下の$p$とすると、

\begin{align}
p &= \frac{n_1p_1 + n_2p_2}{n_1 + n_2}\\
&= \frac{n_1p_1 + kn_1p_2}{n_1 + kn_1}\\
&= \frac{n_1p_1+kn_1p_2}{(k+1)n_1}\\
&= \frac{p_1 + kp_2}{k+1}
\end{align}

独立な2群の比率差 $p_1-p_2$は平均$0 (=p_1-p_2)$, 分散$s^{2}_{p_1 - p_2}$(以下の式)の正規分布に従うので、

\begin{align}
s^{2}_{p_1 - p_2} &= p(1-p)(\frac{1}{n_1} + \frac{1}{n_2})\\
&= p(1-p)(\frac{k+1}{kn_1}) \quad(\because n_2 = kn_1)
\end{align}

$p_1-p_2$を標準化した $z = \frac{p_1 - p_2}{s_{p_1-p_2}}$が近似的に正規分布に従います。ここで、$z$を以下のように変形します。

\begin{align}
z &= \frac{p_1 - p_2}{s_{p_1-p_2}}\\
& = \frac{(p_1 - p_2) - (p_1 - p_2) + (p_1 - p_2)}{s_{p_1-p_2}}\\
& = \frac{(p_1 - p_2) - (p_1 - p_2)}{s_{p_1-p_2}} + \frac{p_1 - p_2}{s_{p_1-p_2}}\\
& = z^{*} + \frac{p_1 - p_2}{s_{p_1-p_2}} \quad( z^{*} = \frac{(p_1 - p_2) - (p_1 - p_2)}{s_{p_1-p_2}} )
\end{align}

(式中の$z^{*}$は、$H_1$が真である場合に標準正規分布に従う統計量です。)
標準正規分布の下側$\alpha/100%$点を$z_{\alpha }$とすると、有意水準$\alpha$で帰無仮説を棄却する確率は$P(z < z_{\alpha })$と表せるので、検出力$1-\beta$を満たすサンプルサイズを知りたい場合、$H_1$が真という条件下で$1 - \beta = P(z < z_{\alpha })$を満たす$n_1(=n_2)$を求めればいいことになります。

先程の式変形より、

\begin{align}
P(z < z_{\alpha }) &= P(z_{*} + \frac{p_1-p_2}{s_{p_1-p_2}} < z_{\alpha })\\
&= P(z_{*} < z_{\alpha } - \frac{p_1-p_2}{s_{p_1-p_2}})
\end{align}

ここで、$P(z_{*} < z_{\beta }) = 1 - \beta $を満たす値$z_{\beta}$を置くと、

\begin{align}
z_{\alpha } - \frac{p_1-p_2}{s_{p_1-p_2}} &= z_{\beta }\\
\frac{p_1-p_2}{s_{p_1-p_2}} &= z_{\alpha } - z_{\beta }\\
s_{p_1-p_2} & = \frac{p_1-p_2}{z_{\alpha }-z_{\beta }}\\
s_{p_1-p_2}^{2} &= (\frac{p_1-p_2}{z_{\alpha }-z_{\beta }})^{2}\\
p(1-p)(\frac{k+1}{kn_1}) &= (\frac{p_1-p_2}{z_{\alpha }-z_{\beta }})^{2}\\
n_1 &= \frac{(k+1)p(1-p)(z_{\alpha }-z_{\beta })^{2}}{k(p_1-p_2)^{2}}
\end{align}

として検出力$1-\beta$を満たすのに必要なサンプルサイズが求まります。

Rサンプルスクリプト1(サンプルサイズの見積もり)

想定される反応率(薬剤の有効率、ECサイトのCVRなど)、有意水準、検出力を指定して、必要なサンプルサイズを見積もるスクリプトです。

# パラメータ設定 -----------------------------------------------------------------
# 比率の設定(p1 < p2 とする)
p1 <- 0.01 # 対照群
p2 <- 0.02 # 処置群

# サンプルサイズの比率の設定
# (対照群 : 処置群 = 1 : k )
k <- 1

# 検定時の有意水準 (片側検定を想定)
a <- 0.05

# type2エラーの確率
b <- 0.2
print(1-b) # 検出力

p <- (p1+k*p2)/(k+1)
za <- qnorm(a)
zb <- qnorm(1-b)

# 処置群、対照群それぞれの必要サンプル数
n1 <- ( (k+1)/k * p*(1-p)*(za-zb)**2 ) / (p1-p2)**2
n2 <- k*n1
print(paste0("対照群: ", round(n1)))
# [1] "対照群: 1520"
print(paste0("処置群: ", round(n2)))
# [1] "処置群: 3040"

Rサンプルスクリプト2(検算)

上記のスクリプト1で見積もったサンプルサイズにした場合に、本当に指定した確率で有意差が検出できるかのテストをしてみます。検出力80%としてサンプルサイズを見積もったので、検定を100回やったらそのうち80回程度はp値が有意水準を下回る結果になります。

# 実際に検出できるかテスト ------------------------------------------------------------
# 反応率、サンプルサイズに基づいてデータ生成し、χ二乗検定のp値を出力する関数
trial <- function(p1, p2, n1, n2) {
  # データ生成
  x1 <- rbinom(n1, 1, p1)
  x2 <- rbinom(n2, 1, p2)
  # クロス集計表
  dat <- matrix(c(sum(x1), n1-sum(x1), sum(x2), n2-sum(x2)), ncol = 2)
  # χ二乗検定
  res <- chisq.test(dat, correct=F) # correct=Fはイェーツの補正をしないという意味
  return(res$p.value)
}


# 比率の設定(p1 < p2 とする)
p1 <- 0.01 # 対照群
p2 <- 0.02 # 処置群

# 検定時の有意水準 (片側検定を想定)
a <- 0.05

# サンプルサイズの指定
n1 <- 1520 # 上記のスクリプトで求めた値を指定
n2 <- 3040

# 検定の回数
n <- 100

# n回検定してみた結果(p値)を取得
res <- mapply(trial, rep(p1, n), rep(p2, n), rep(n1, n), rep(n2, n))

res <- data.frame(p_value=res) %>% 
  dplyr::mutate(type2_error=ifelse(p_value > a, 1, 0)) # 帰無仮説が棄却されない場合を1とする

table(res$type2_error)
# 0  1 
# 79 21 
# 100回検定した中で79回(80%程度)は帰無仮説を棄却できている
# つまり、80%程度の検出力になっている

Rサンプルスクリプト3(検出力とサンプルサイズの関係)

検出力が高いほど、必要となるサンプルサイズは大きくなりますが、検出力を上げていった場合に必要サンプルサイズがどう推移していくのかを試しに計算してみます。

# 検出力とサンプルサイズの関係 ----------------------------------------------------------
# 反応率、有意水準、検出力、処置群に対する対照群の比率に基づいてサンプルサイズを計算する関数

sample_size <- function(p1, p2, a, pow, k) {
  # p1 :対照群
  # p2 :処置群

  # サンプルサイズの比率の設定
  # (対照群 : 処置群 = 1 : k )

  # a: 検定時の有意水準 (片側検定を想定)
  # pow: 検出力

  p <- (p1+k*p2)/(k+1)
  za <- qnorm(a)
  zb <- qnorm(pow)

  # 処置群、対照群それぞれの必要サンプル数
  n1 <- ( (k+1)/k * p*(1-p)*(za-zb)**2 ) / (p1-p2)**2 # 対照群
  n2 <- k*n1 # 処置群

  return(c(n1, n2))
}

p1 <- 0.01 # 対照群
p2 <- 0.02 # 処置群

# サンプルサイズの比率の設定
# (対照群 : 処置群 = 1 : k )
k <- 1 # 対照群と処置群が同数であるとする

# 検定時の有意水準 (片側検定を想定)
a <- 0.05

# 検出力を0.1から0.99まで変える
pow_vec <- seq(from=0.1, to=0.95, length=19)
pow_vec <- append(pow_vec, 0.99)

n <- length(pow_vec)

res <- mapply(sample_size, 
              rep(p1, n), 
              rep(p2, n), 
              rep(a, n), 
              pow_vec, 
              rep(k, n))

res <- res %>% 
  t() %>% 
  data.frame()
colnames(res) <- c("control", "target")
res$power <- pow_vec

# 可視化
ggplot(res, aes(x=power, y=target)) + 
  theme_bw() + 
  geom_line() + 
  geom_point()

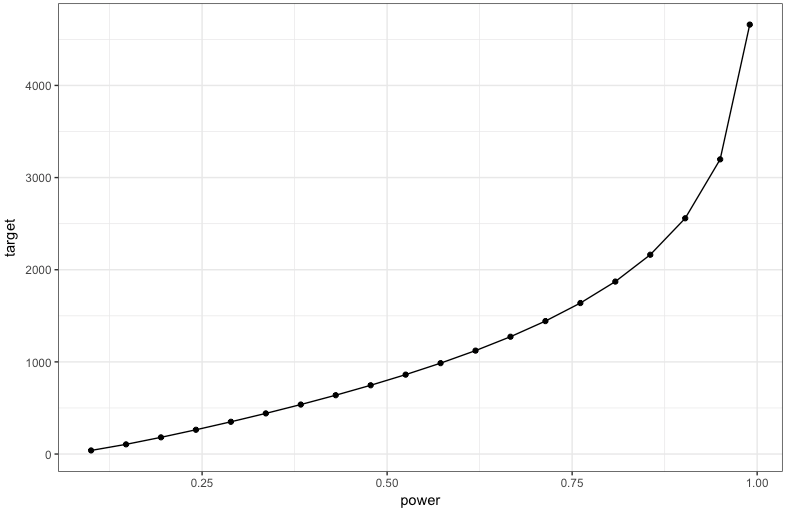
スクリーンショット 2021-01-31 16.46.55.png
横軸が検出力で縦軸がサンプルサイズです。ここでのサンプルサイズは対照群と処置群が同数であるとしたときの、片方のグループに必要な人数です。
検出力が1に近づくにつれ急激に必要サンプルサイズが上がっていきます。なお、検出力を100%にしようとすると必要サンプルサイズは計算上、無限になります。

対照群を少なめにして処置群を多めに取りたい、という場合については、処置群人数=対照群人数の場合に比べて必要となるサンプルサイズが変わってきます。試しに、対照群に対する処置群の比率を1〜5まで変えた場合に、必要サンプルサイズがどうなるか計算しました。

# 対照群と処置群のサンプルサイズが等しくない場合
# 対照群に対する処置群の比率を1〜5まで変えた時の必要なサンプルサイズを計算
# p1, p2, a, power_vecの値はスクリプト2で設定した値を使う
for (i in 1:5) {
  res <- mapply(sample_size, 
                rep(p1, n), 
                rep(p2, n), 
                rep(a, n), 
                pow_vec, 
                rep(i, n))

  res <- res %>% 
    t() %>% 
    data.frame()
  colnames(res) <- c("control", "target")
  res$power <- pow_vec
  res$k <- i

  if (i == 1) {
    result <- res
  } else {
    result <- result %>% 
      dplyr::bind_rows(res)
  }
}

result$k <- as.factor(result$k)

# 可視化
ggplot(result, aes(x=power, y=target, group=k, colour=k)) + 
  theme_bw() + 
  geom_line() + 
  geom_point()

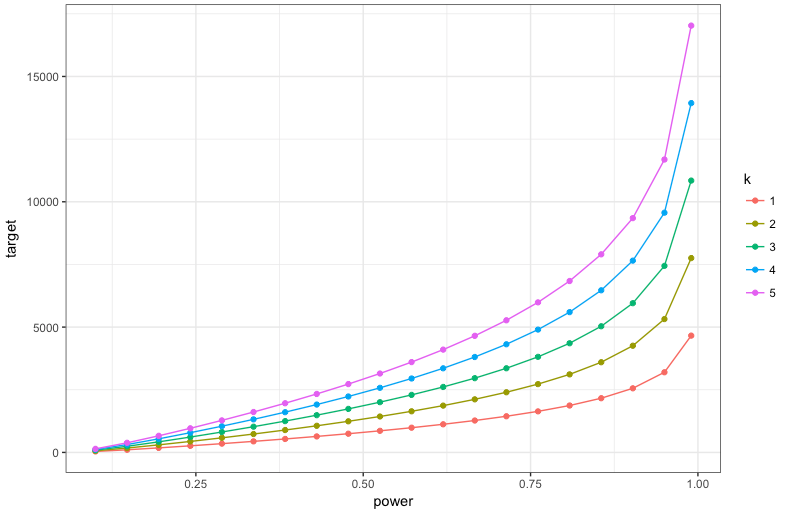
スクリーンショット 2021-01-31 16.59.45.png
先程の図と同様、横軸が検出力で縦軸が必要となる処置群のサンプルサイズです。凡例にあるkというのが、対照群に対する処置群の比率を表しています。
処置群と対照群の構成比率が1:1から離れて割付比率の差が広がるほど、同じ検出力でも必要となるサンプルサイズが大きくなることがわかります。

参考までに、検出力=0.9のときの各サンプルサイズを切り出すと以下の通りでした。
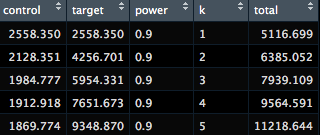
スクリーンショット 2021-01-31 17.08.54.png
(control, targetがそれぞれ対照群、処置群のサンプルサイズ、kが割付比率、totalが合計の必要サンプルサイズです)

終わりに

実務の上では様々な制約があり十分なサンプルが集まらないことも多いと思います。そういう時はベイズABテストという便利な方法があるのでそちらも試すと良いのかもしれません。

今回、教科書や論文を参照しつつまとめましたが、自己流な部分もあるのでもし間違いなどあればご指摘いただけると幸いです。

参考文献

3
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
3