![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
はじめに
街並みが夕暮れに化粧をし始めた今日この頃、皆様いかがお過ごしでしょうか?
六花 牡丹(りっか ぼたん)と申します ![]()
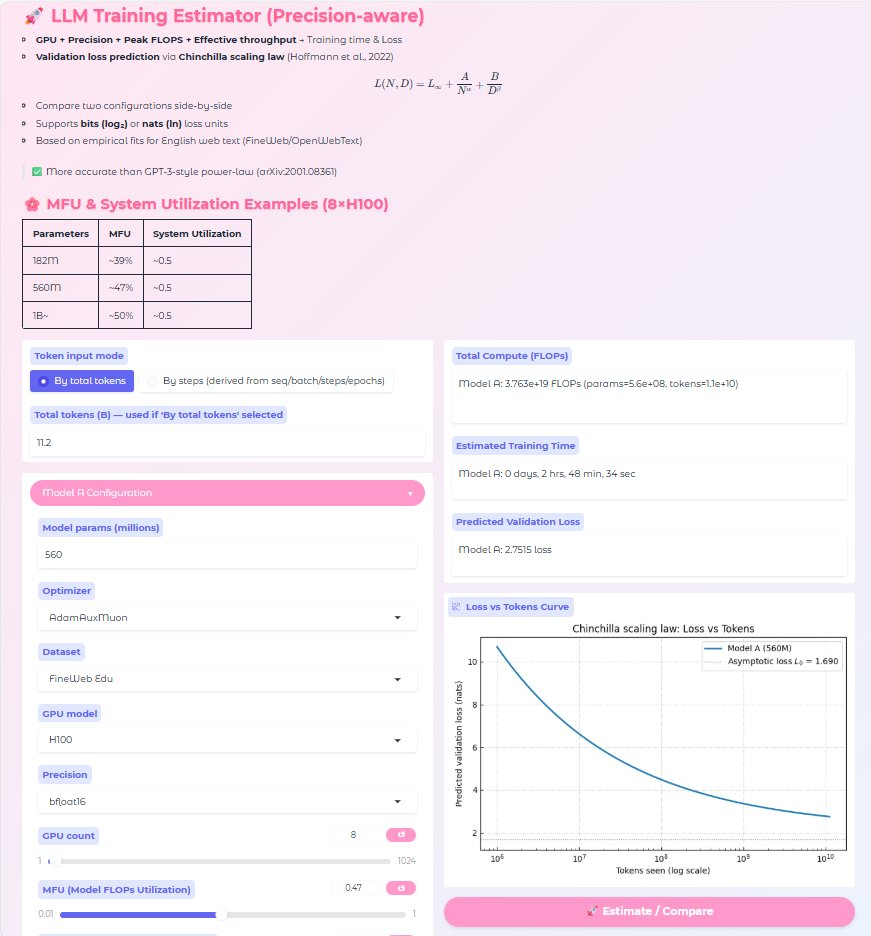
LLM Training Estimatorという、Chinchilla スケーリング則に基づく、学習時間・loss予測アプリを開発しました。
本記事では、その詳細についてお話しいたします。
概要
本記事では、LLM(大規模言語モデル)のトレーニングに必要な 計算量(FLOPs)・所要時間・検証損失 を、GPU の精度(float16, bfloat16, FP8 など)やシステム効率(MFU, Utilization)を考慮して 高精度に予測する Gradio アプリを紹介します。このアプリの核心となる理論は、Chinchilla スケーリング則(Hoffmann et al., 2022)であり、実際の実験を通じて得たloss, MFUなどの知見を反映しています。
🔗 論文: Hoffmann, J. et al. (2022). Training Compute-Optimal Large Language Models. arXiv:2203.15556
アプリの開発動機
LLM学習において誤差・学習時間が予測できれば、進捗把握や評価が早期に可能になることから、開発を行いました。
アプリの主な機能
- GPU + 精度ごとの理論ピーク FLOPS をアプリに内包し、選択するだけで完結できるようにしました。(H200, B200, RTX 5090 など最新 GPU サポート)
- 複数のモデルのトレーニング設定を比較可能(パラメータ数、GPU構成、バッチサイズなど)
- Chinchilla スケーリング則 を用いた検証損失の予測(ビット単位 or 自然対数単位)
- データセット・オプティマイザの効率係数 を考慮(例:FineWeb vs OpenWebText)
- トレーニング所要時間の推定(MFU × システム利用率を考慮)
- 損失 vs 学習トークン数の可視化プロット
Chinchilla スケーリング則の数学的背景
1. スケーリング法則の基本形
Hoffmann et al. (2022) において、大規模言語モデルの検証損失 $ L $ が、モデルパラメータ数 $ N $ と 学習トークン数 $ D $ の関数として次のように近似できると示されました。
L(N, D) = L_\infty + \frac{A}{N^\alpha} + \frac{B}{D^\beta}
ここで:
- $ L_\infty $:データ・モデルが無限大のときの 不可避損失(irreducible loss)
- $ A, B $:それぞれモデル・データ規模の影響係数
- $ \alpha, \beta $:べき乗則の指数(論文(Hoffmann et al. (2022))では $ \alpha \approx 0.34, \beta \approx 0.28 $)
この式は、交差エントロピー損失(単位:nat または bit) で表されます。アプリでは、デフォルトで 自然対数単位(nats, $ \ln $)を使用し、必要に応じてビット単位($ \log_2 $)に変換することができます。
💡 ビット単位の損失 ⇔ nats 単位の損失の関係:
\text{loss}_{\text{bits}} = \frac{\text{loss}_{\text{nats}}}{\ln 2} \approx \text{loss}_{\text{nats}} \times 1.443
アプリにおける損失予測式
アプリの predict_val_loss_chinchilla() 関数では、上記の理論式を基に下記のようにLossを予測します。
L(N, D) = L_\infty + \frac{A}{(N)^\alpha} + \frac{B}{\left( D \cdot f_{\text{dataset}} / f_{\text{optimizer}} \right)^\beta}
-
データセット係数 $ f_{\text{dataset}} $:高品質データ(FineWeb)は $ f = 1.0 $、低品質(OpenWebText)は $ f = 0.14 $
(この係数はNanoGPTの収束速度の結果から導いています。) -
オプティマイザ係数 $ f_{\text{optimizer}} $:AdamW は収束効率が低いため補正(例:
1.927)
(Muonから効率を参照しています。)
これは、有効学習トークン数(effective tokens)の概念を導入し、実質的な情報量を考慮する工夫です。
計算時間の推定原理
トレーニング時間 $ T $ は次式で推定されます。
T = \frac{C}{\text{Effective FLOPS}} = \frac{N \cdot D}{G \cdot F_{\text{peak}} \cdot \text{MFU} \cdot U}
- $ G $:GPU 台数
- $ F_{\text{peak}} $:1 GPU のピーク FLOPS(精度依存)
- MFU(Model FLOPs Utilization):モデル演算の理論最大に対する実効利用率(0–1)
- U(Utilization Overhead):通信・I/O・バッチ待ちなどのシステムオーバーヘッド
例:8×H100(FP8, 3.958e15 FLOPS)で MFU=0.35, U=0.5 → 実効性能 ≈ 5.5e15 FLOPS
H100を用いた実験では、MFUはおおよそ下記のようになりました。
| Parameters | MFU | System Utilization |
|---|---|---|
| 182M | ~39% | ~0.5 |
| 560M | ~47% | ~0.5 |
| 1B~ | ~50% | ~0.5 |
可視化:損失 vs トークン数
アプリは、指定モデルサイズに対して 損失曲線 $ L(D) $ をプロットします。これにより、
- 学習が「飽和」するトークン数の把握
- データ効率の比較(例:Model A vs Model B)
- $ L_\infty $ への収束挙動の確認
が可能になります。
予測の精度
nanochatにおける条件を試しに入力すると、
- 560M
- 11.2B tokens
- AdamAuxMuon
- Fineweb Edu
- 8×H100
Time: 2h48m, validation loss: 2.75
となり、実測値とほぼ一致します。
実測値に関しては下記リポジトリをご参照ください。
参考論文・サイト等
Training Compute-Optimal Large Language Models, https://arxiv.org/abs/2203.15556
Chinchilla スケーリング則の原論文です。
Scaling Laws for Neural Language Models, https://arxiv.org/abs/2001.08361
$ L \propto N^{-\alpha} D^{-\beta} $ を示している論文です。
Efficient Large-Scale Language Model Training on GPU Clusters, https://arxiv.org/abs/2104.04473
MFU の定義と実測値を示している論文です。
Muon is Scalable for LLM Training, https://arxiv.org/abs/2502.16982
Muon Optimizerが大規模モデルにおいても有効であることを示した論文です。
執筆者:六花 牡丹(りっか ぼたん)
おさげとハーフツイン・可愛いお洋服が好きで、基本的にふわふわしている変わり者。
結構ドジで何もないところで転ぶタイプ。
人工知能に関しては独学のみ。