前回、散布図を出力することをしたので、今回はもう少し具体的なデータを使って、
散布図だけでなく、回帰分析を行おうと思います。
今回は、特徴量が一つしかないときの回帰から始めます。
用いるデータ
https://sites.google.com/site/datajackets/data-jackets/list2/dj0514
のサイトにある、https://vincentarelbundock.github.io/Rdatasets/csv/datasets/airmiles.csv
こちらよりダウンロードできるCSVファイルを利用しようと思います。
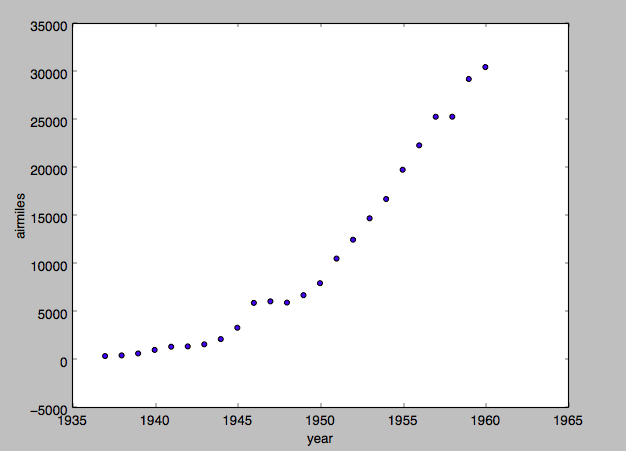
こちらは1937年から1960年の各年の、合州国の商用航空会社の課税利用者マイル数のデータです。
まずは散布図を書いてみる。
前回のコードを使って、散布図を出力してみます。
from matplotlib import pyplot as plt
import numpy as np
def main():
data = np.genfromtxt("airmiles.csv",delimiter=",", skiprows=1)
plt.scatter(data[:,1], data[:,2])
plt.xlabel('year')
plt.ylabel('')
plt.show()
if __name__ == '__main__':
main()
出力結果はこちら
このような形になると思います。
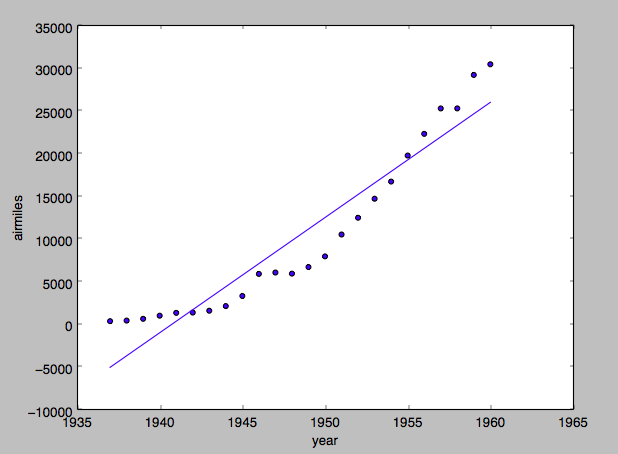
散布図を確認できたところで、回帰直線を引いてみます
回帰直線を引こう!
まずはコードを示します。
from matplotlib import pyplot as plt
import numpy as np
def main():
data = np.genfromtxt("airmiles.csv",delimiter=",", skiprows=1)
x = data[:,1]
y = data[:,2]
A = np.array([x,np.ones(len(x))])
A = A.T
m,c = np.linalg.lstsq(A,y)[0]
plt.scatter(x, y)
plt.xlabel('year')
plt.ylabel('airmiles')
plt.plot(x,(m*x+c))
plt.show()
if __name__ == '__main__':
main()
出力結果はこちら
そのデータに当てはめた直線を描画しています。最小二乗法による回帰です。
さて、こちらにあらたなコードがあることに気づくと思います。
A = np.array([x,np.ones(len(x))])
A = A.T
m,c = np.linalg.lstsq(A,y)[0]
この辺は詳しくはググっていただくとして、(自分もよくわからないので理解し次第、解説追加します。)
np.linalg.lstsq
こちらの関数について解説します。
これはnumpyに含まれるlinear algebra(線形代数)に関するモジュールで、どういう関数を持つかは
こちらhttp://docs.scipy.org/doc/numpy-1.10.1/reference/routines.linalg.html
に詳しくあります。
lstsqというのは least-squareを略したもので、日本語で「最小二乗法」と呼ばれます。
「測定で得られた数値の組を、適当なモデルから想定される1次関数、対数曲線など特定の関数を用いて近似するときに、想定する関数が測定値に対してよい近似となるように、残差の二乗和を最小とするような係数を決定する方法」
(Wikipediaより)
今回はこの最小二乗法により
傾き: 1350.28173913
切片: -2620496.13536
と算出されました。
次回は複数の特徴量に関する分析(多次元回帰)について取り扱いたいと思います。