だいたい自分用メモ. プログラミングからPythonから競プロからDPまで何もかも初心者なので、何もかも間違っている可能性有り.
問題概要#
$l$から$r$までの範囲の皿に乗っているみかんを、1皿につき$x$個ずつ(但し、皿に載っているみかんの数を超過してはならない)ガバーッと食べたときの最大個数を求める.
要するに、$A_i$のヒストグラムの中に書くことのできる長方形のうち、最も面積が大きいものはどれかを求めればいいということ.
《イメージ図(N=6, A=[2,4,4,9,4,9]が与えられた場合)》
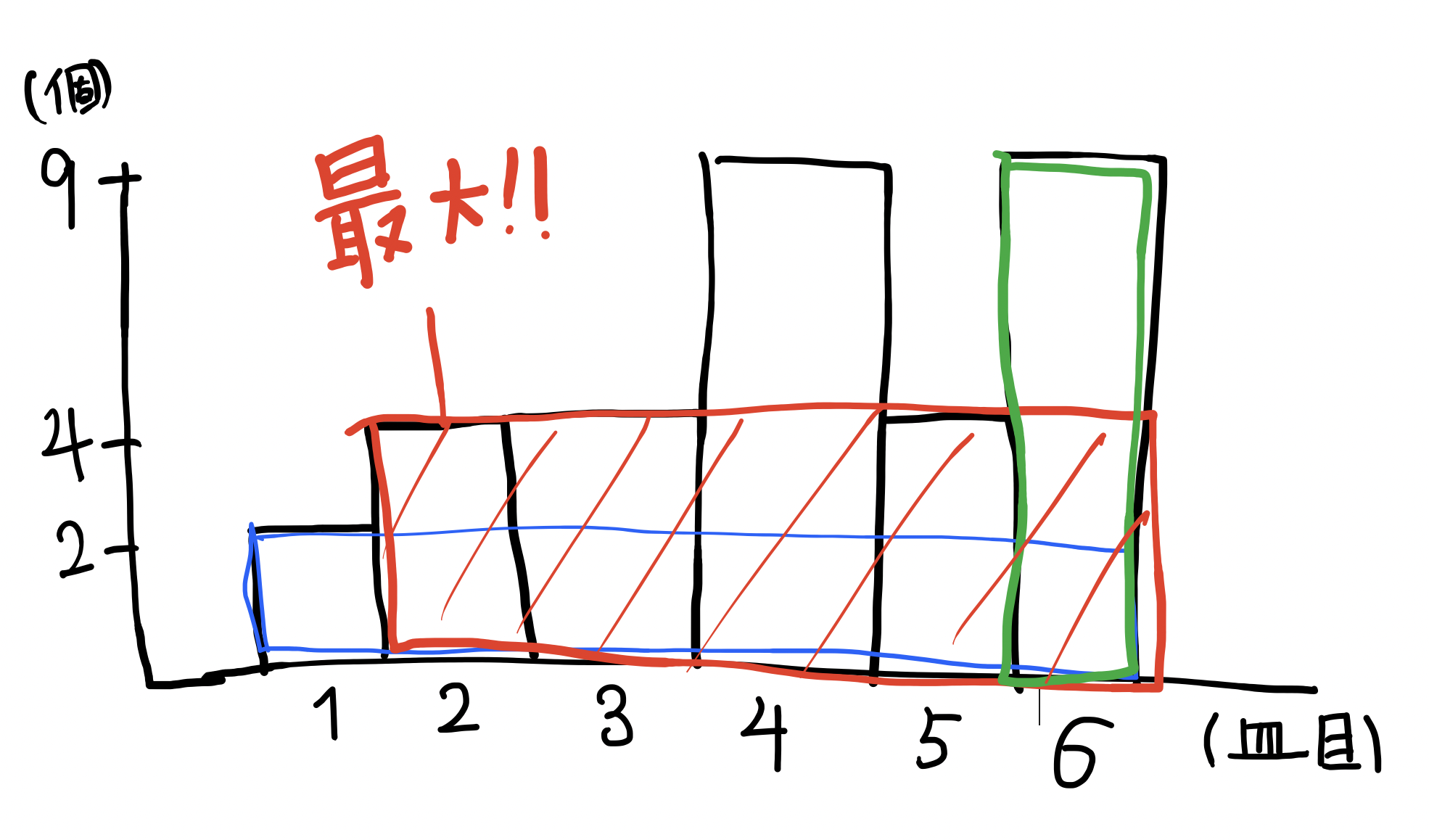
板タブで描くの難しいですね.
考えたこと#
つい先日一次元配列を用いたDP(カエルのやつ)をなんとか理解したところだったので、その練習ついでに、二次元配列を使ったDP(メモ型回帰?)で解いてみようと考えた(でもDPのことまだ何も分かってないので、この解き方がDPなのかどうか分からないです).
例えばA=[2,4,4,9,4,9]が与えられたとして、Aの1番目から3番目までを切り出して作る長方形の高さは、
- 1番目のみで作れる長方形の高さは2(これをH[0]とする)
- 1から2番目の中で作れる長方形の高さはH[0]とA[1]の小さい方(=H[1])
- 同様に、1から3番目の中で長方形の高さはH[1]とA[2]の小さい方
という流れで求められるので、それらを二次元配列に記録したいということ.
(日本語が下手)
やってみたこと1#
N = int(input())
A = [int(i) for i in input().split()]
dp = [[0]*(N) for j in range(N)] # 配列を作る
for i in range(N):
dp[i][i]=A[i]
# 1皿のみの場合、長方形の高さは林檎の個数と等しい
for left in range(N):
for right in range(left+1,N):
dp[left][right]=min(dp[left][right-1],A[right])
# [right-1]皿前まで選んだ場合の高さと[right]皿目の林檎の個数を比較して、小さい方で更新
for left in range(N):
for right in range(left,N):
x = dp[left][right]
ans = max((right+1-left)*x,ans)
#dpで求めた長方形の高さと横の長さを掛け、面積の最大値を求める
print(ans)
A=[2,4,4,9,4,9]として、
dpを出力するとこんな感じになります.
[[2, 2, 2, 2, 2, 2],
[0, 4, 4, 4, 4, 4],
[0, 0, 4, 4, 4, 4],
[0, 0, 0, 9, 4, 4],
[0, 0, 0, 0, 4, 4],
[0, 0, 0, 0, 0, 9]]
i行は「i番目の皿から始めたときの長方形の高さ」で、
j列は「j番目の皿までを選んだときの長方形の高さ」を意味しています.
つまり、左上から4行目4列目の9は「4番目の皿から4番目の皿までで作れる長方形の高さ」であり、その右の4は「4番目の皿から5番目の皿までで作れる長方形の高さ」を表していることになります.
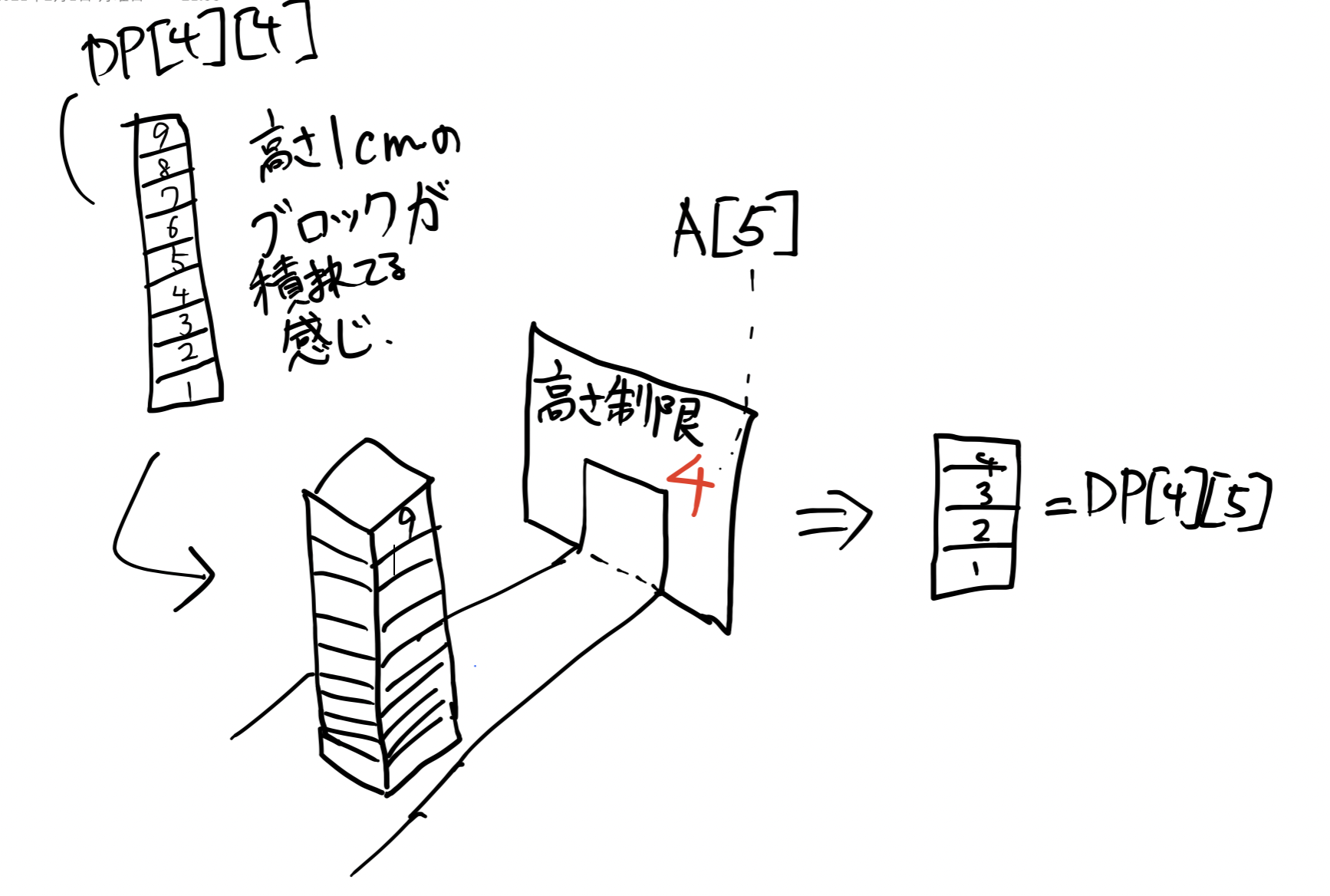
肝心のdp[left][right]=min(dp[left][right-1],A[right])の部分なのですが、ベルトコンベアに流されてどんどん高さ制限のゲートに削られていくイメージです.
(ゴミみたいな図を書いてしまい申し訳ございません)
やってみたこと2#
良く考えたらこんなにfor並べる必要なくない?と思ってまとめたコード.
N = int(input())
A = [int(i) for i in input().split()]
dp = [[0]*(N) for j in range(N)]
ans = 0
for left in range(N):
dp[left][left]=A[left]
for right in range(left,N):
if right!=left:
dp[left][right]=min(dp[left][right-1],A[right])
x = dp[left][right]
ans = max((right+1-left)*x,ans)
print(ans)
スッキリはしたけど、dp[left][left]=A[left]は何をやっているのかめちゃめちゃわかりづらい気もする.
まとめ#
DPは難しい...