はじめに
量子アニーリング、シミュレーテッドアニーリング、QUBO等については
量子アニーリング、イジングモデルとフレームワーク
をご参照ください。
個別指導塾をモチーフに、時間割を作成する際に発生する様々な制約条件をQUBO形式に落とし込み、アニーリングを行うことで最適な時間割を作成してみたいと思います。
今回はwildcatライブラリを利用して、シミュレーテッドアニーリングを行います。
wildcatライブラリの使い方、インストールはこちら。 https://github.com/mdrft/wildcat
なお、この問題を解くにあたって、下記の記事を大いに参考にさせて頂きました。
wildcatで巡回セールスマン問題を試してみた
wildcatで4x4の数独を解いてみた
QUBOを使って日本地図の彩色問題やってみた
python3のインストールはこちらから。
https://www.anaconda.com/download/
問題設定
以下の状況をイメージしてみます。今回は1回目ということで、かなり簡単な問題設定にしてみました。
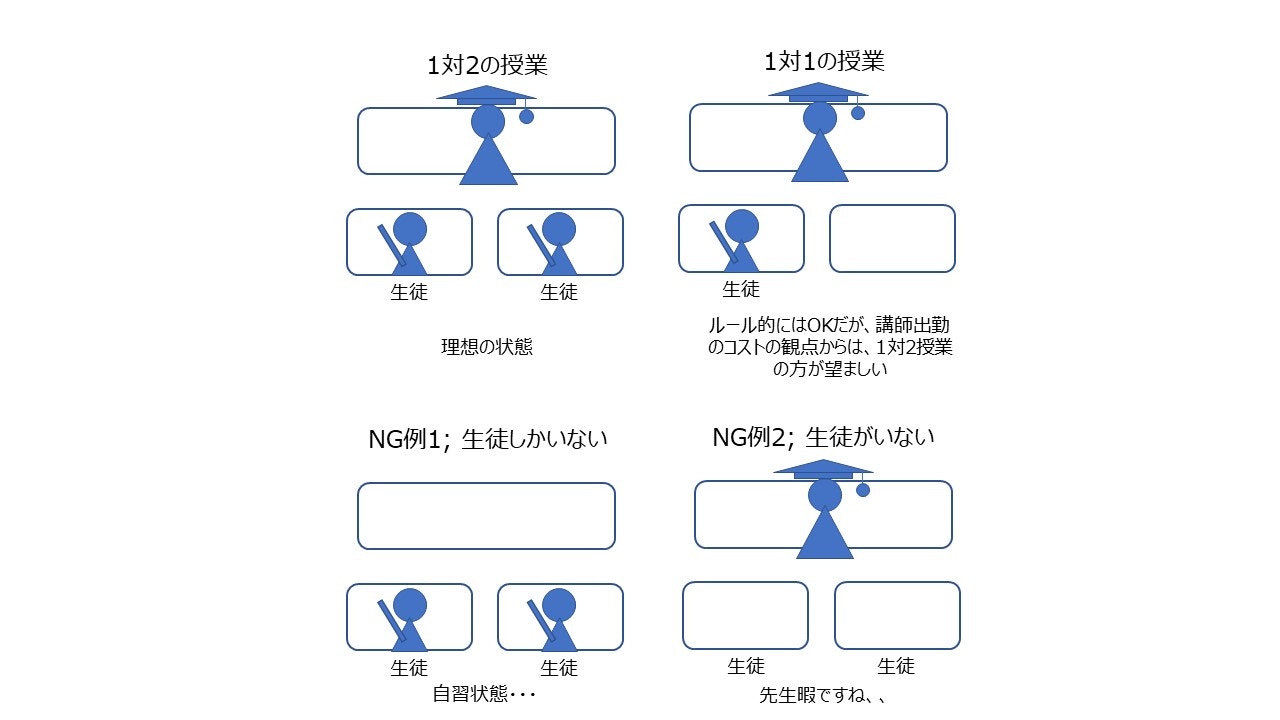
・ここの個別指導塾では講師一人に対して、生徒がを2人まで同一時間内で担当することができる(1対2授業)。1対1授業もしてもよいが、講師の出勤にはコストがかかることを加味すると、1対1授業はなるべく削減したい。なお、生徒しかいない場合、講師しかいない場合はルール違反。
【時間の設定】講習は1日限り。13時スタート~16時スタートまでの計4コマの中で時間割を組むことにする。
【教室の設定】教室に設置されたブースは1つ。(後々拡張予定)
【講師の設定】講師はA, Bの2名がいることにする。
【講師の出勤可能時間について】講師Aは13時、14時のコマしか出勤できない。講師Bは逆に15時、16時のコマしか出勤できない
【生徒の設定】太郎君、次郎君の2人が参加。二人に時間的制約はない。
【生徒の授業数】太郎君は3コマの授業を、次郎君は2コマの授業を受講する。なお、ここでは科目の概念は考えない。
【その他】生徒-講師の相性などはここでは考慮しないことにする。また、場合によってはいわゆる「空きコマ」が発生してしまうこともあるが、これも今回は考慮しない。
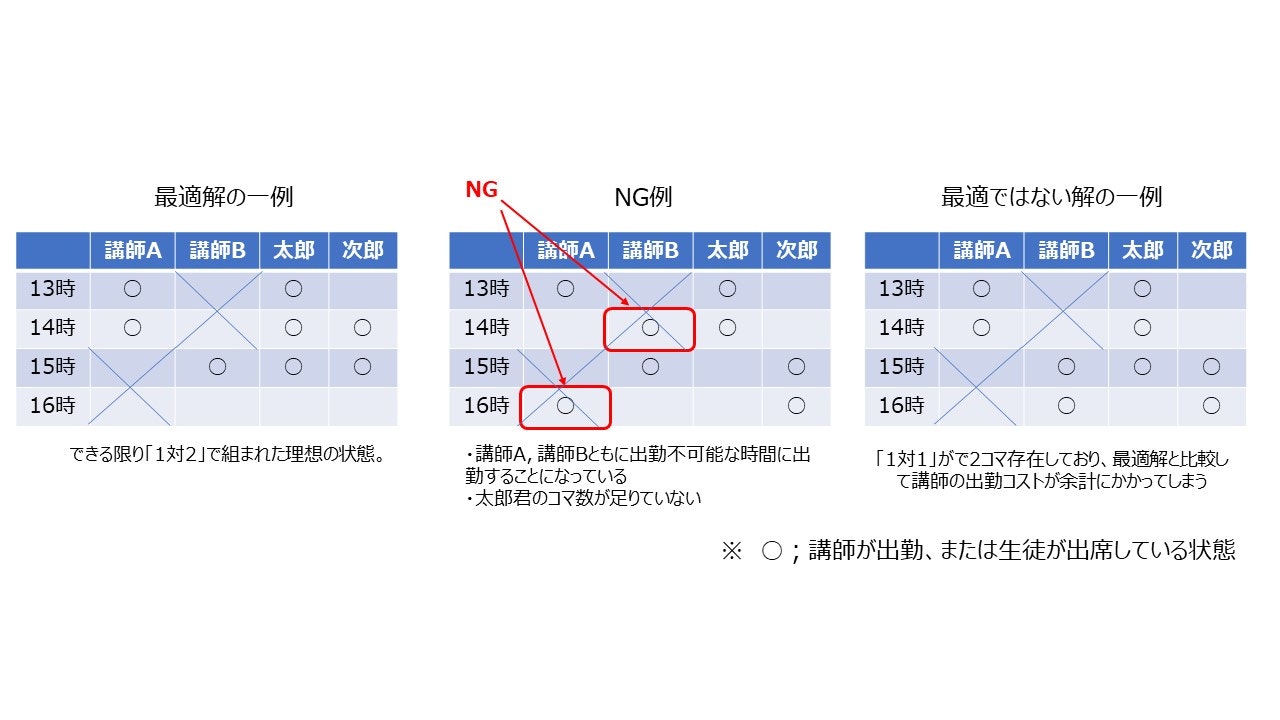
最適解、NG例の一例は下のようになります。まぁこのレベルだったら人間がやった方が遥かに速いんですけどね。笑 はたして今回は最適解にたどり着けるのでしょうか。或いはNG例になってしまうのか。はたまた最適ではない解に落ち着いてしまうのか・・・確認していきます。
マッピング
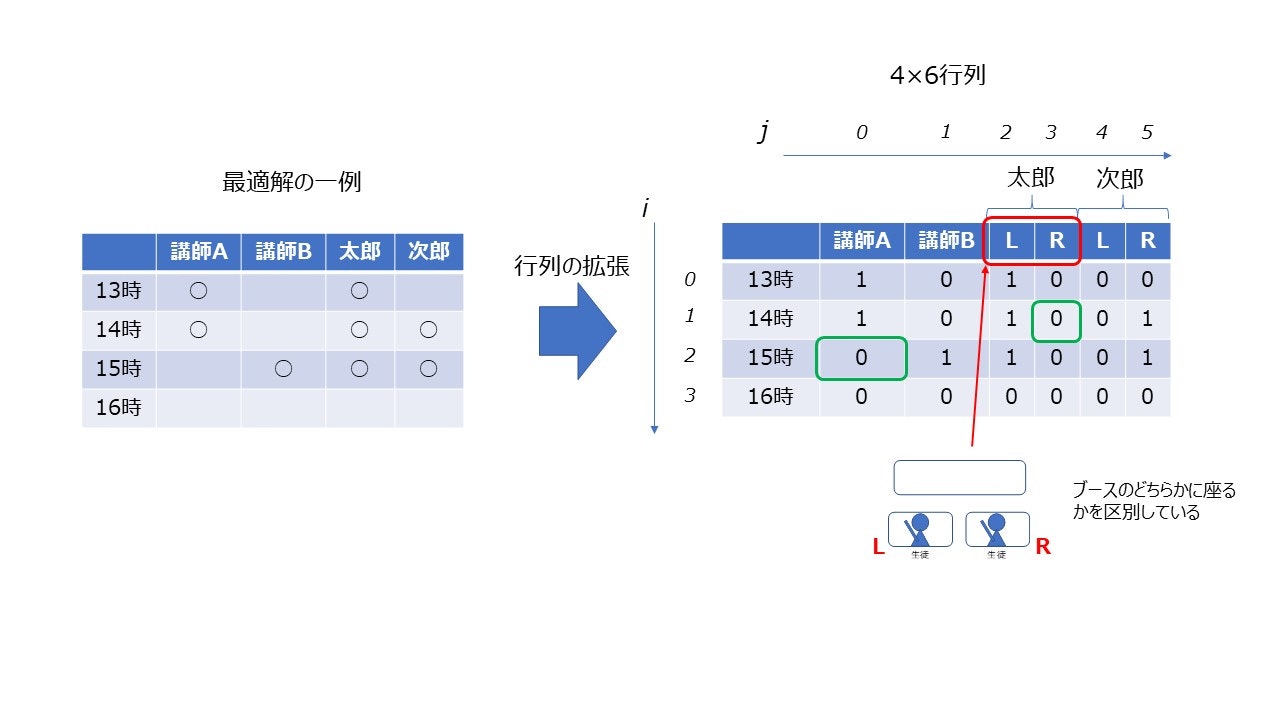
QUBOにマッピングを行うために、下図右のように行列を少し変更します。行列の要素は0か1二変数しかとることが許されないため、太郎君、次郎君の列を増やしました。太郎君次郎君がブースの左側(L)に座るのか、右側(R)に座るのかを区別して考えることで、各要素を二変数で表現することが可能になります。
以降はwildcatで巡回セールスマン問題を試してみた
の方法にのっとって、ハミルトニアン$H$を
$$H=\sum_{i_1,j_1,i_2,j_2}J_{{i_1},{j_1},{i_2},{j_2}}x_{{i_1},{j_1}}x_{{i_2},{j_2}}$$
の形式で表示し、それをQUBOに変換すれば、アニーリングを実施することができます。なお、ここで$J_{{i_1},{j_1},{i_2},{j_2}}$はCell($i_1$,$j_1$)とCell($i_2$,$j_2$)の相互作用を表します。例えば$J_{2,0,1,3}$はCell(2,0)とCell(1,3)の相互作用の強さを表すことになります(上図の緑枠に相当するCell)。
相互作用(制約条件)の設定
あとは、「問題設定」で想定した状況を相互作用$J$(制約条件とも呼ぶ)に過不足なく取り込んでいきます。初期状態では、$J=0$のため、
# 行列の数
N = 4 #行の設定
M = 10 #列の設定
# 行列Jを設定
J = np.zeros((N, M, N, M), dtype = np.float32)
とし、相互作用を取り込んでいきます。ここでMの値を6ではなく10とした理由は後述します。
ルール1:講師A, Bは同時に存在できない
同じ時間帯に講師A, 講師Bが存在することはできませんから、例えば$x_{0,0}$と$x_{0,1}$が同時に1になってしまったときにペナルティ$A$を課します。この場合、$x_{0,0}$と$x_{0,1}$の少なくとも一方が0であれば、ペナルティを回避することができます。
つまり、
$$i_1=i_2, j_1=0, j_2=1$$
を満たす$J_{{i_1},{j_1},{i_2},{j_2}}$にペナルティ$A$を課します。
# 定数の定義
A = 10 #ペナルティの値
# ルール1:講師A, Bは同時に存在できない
for i1 in range(N):
J[i1, 0, i1, 1] += A
こんな感じです。ペナルティの値は適当に10としました。
ルール2~6の設定
ルール1と同様のルールが他にもあるので、一気に書き下します。
for i1 in range(N):
# ルール2:ブースLに太郎と次郎は同時に存在できない
J[i1, 2, i1, 4] += A
# ルール3:ブースRに太郎と次郎は同時に存在できない
J[i1, 3, i1, 5] += A
# ルール4:ブースLとRを太郎は同一時間に占有できない
J[i1, 2, i1, 3] += A
# ルール5:ブースLとRを次郎は同一時間に占有できない
J[i1, 4, i1, 5] += A
講師の出勤不可時間はこんな感じで設定します。
# ルール6: 講師Aは13時、14時のコマしか出勤できない。講師Bは逆に15時、16時のコマしか出勤できない
J[2, 0, 2, 0] += A
J[3, 0, 3, 0] += A
J[0, 1, 0, 1] += A
J[1, 1, 1, 1] += A
ルール7: 太郎君と次郎君の授業数を設定する
この制約の設定は、
物理のいらない量子アニーリング入門
中にでてくるセールスマン問題のQUBO第二項
「同時刻にセールスマンはどこかの1都市にしかいない 」
と同様に考えます。
太郎君は3コマの授業をとるということは、
\sum_{j=2,3}\sum_{i=0}^{3}x_{i,j}=3\\
を満たさなければなりません。これを
\biggl(
\sum_{j=2,3}\sum_{i=0}^{3}x_{i,j}-3
\biggr)^2=0
のように式変形することで、太郎君の受講するコマ数が3コマ未満の場合でも、4コマ以上の場合でも左辺の値は0より大きくなり、ペナルティを設定することができます。
$J$の形式で表すと、
J(taro)=A\sum_{{j_1}=2,3}\sum_{{j_2=2,3}}\sum_{{i_1},{i_2}}
(1-6\delta_{i_1,i_2}\delta_{j_1,j_2})x_{i_1,j_1}x_{i_2,j_2}+9A
と書けます。ここで$\delta_{i_1,i_2}$はクロネッカーデルタであり、また
${x_{i,j}}^2=x_{i,j}$を利用しています。
2コマの授業をとる次郎君も同様に
J(jiro)=A\sum_{{j_1}=4,5}\sum_{{j_2=4,5}}\sum_{{i_1},{i_2}}
(1-4\delta_{i_1,i_2}\delta_{j_1,j_2})x_{i_1,j_1}x_{i_2,j_2}+4A
のように書けます。コーディングは下記のような感じです。なお、参考資料にもあるように、定数項は落としています。
# ルール7:生徒のコマ数の制約条件
## 太郎は3コマの授業をとる
for i1 in range(N):
for j1 in range(2,4):
for i2 in range(N):
for j2 in range(2,4):
J[i1, j1, i2, j2] += A - 6 * A * delta(i1, i2) * delta(j1, j2)
## 次郎は2コマの授業をとる
for i1 in range(N):
for j1 in range(4,6):
for i2 in range(N):
for j2 in range(4,6):
J[i1, j1, i2, j2] += A - 4 * A * delta(i1, i2) * delta(j1, j2)
ルール8の設定、でもその前に。
さて、いよいよ
「講師一人に対して、生徒がを2人まで同一時間内で担当することができる。講師がいないときに生徒がいるとペナルティ、その逆もまたペナルティ」
という制約条件を考えます。
今回の制約条件は、講師A,講師B,更には太郎君と次郎君全員が係わるいわゆる「多体」の相互作用となります。ここでは、
イジング模型への変換
で紹介されている「次数下げ」のテクニックを利用して、多体問題をQUBO形式に変形していきます。
今回は、下図のようにj=6~9の列を新たに追加することでこの問題に対応します。列数Mを6ではなく10としたのは、この為でした。
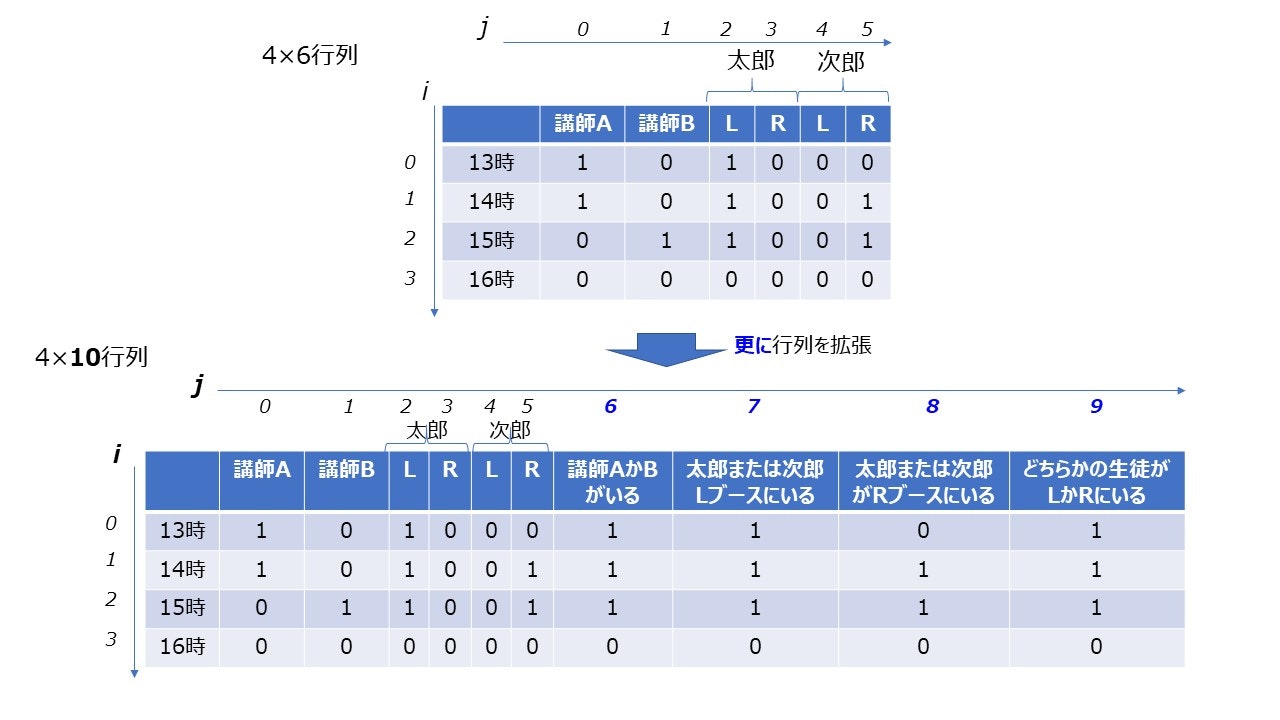
j=6 の列・・・講師AかBのどちらかが出勤していれば1を返すセル
j=7 の列・・・L側のブースに生徒どちらかがいれば1を返すセル
j=8 の列・・・R側のブースに生徒どちらかがいれば1を返すセル
j=9 の列・・・Lブース、Rブースどちらかに生徒がいれば1を返すセル
要は$x_{j=6}$は$x_{j=0}$と$x_{j=1}$のOR関数になるわけです。
$x_{j=6}$がそのような関数になるためには適切な制約条件を追加すればよく、結論を書くと
$$H_p=x_{j=0}+x_{j=1}+x_{j=6}+x_{j=0}x_{j=1}-2x_{j=0}x_{j=6}-2x_{j=1}x_{j=6}$$
となります。(ちなみに私はこれをうまく導出する方法がわからず、係数を片っ端から代入して調べ上げました。。。)
念のため$x_{j=0}$,$x_{j=1}$,$x_{j=6}$に 0 or 1 を代入してペナルティ値を確認していきましょう。$x_{j=6}$が$x_{j=0}$,$x_{j=1}$に対してOR関数を満たすときのみ、ペナルティが0になっていることがわかります。
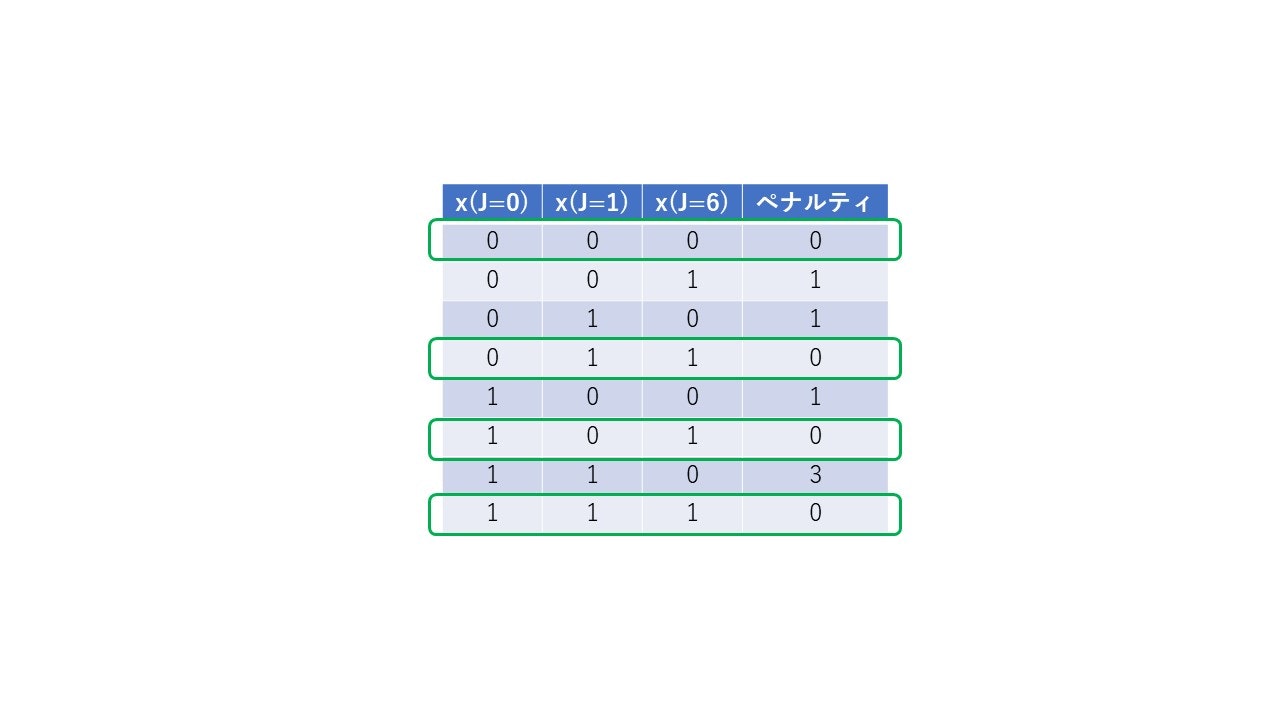
j=6~9のペナルティの設定を一気に書き下すと、こんな感じになります。
# ルール8:生徒がいるときは必ず講師がいる。3体問題に置き換えて解いていく
## x_j=6 :x_j=0とx_j=1(講師Aと講師B)のOR関数
for i1 in range(N):
J[i1, 0, i1, 0] += A
J[i1, 1, i1, 1] += A
J[i1, 6, i1, 6] += A
J[i1, 0, i1, 1] += A
J[i1, 0, i1, 6] -= 2 * A
J[i1, 1, i1, 6] -= 2 * A
## x_j=7 :x_j=2とx_j=4(ブースL)のOR関数
for i1 in range(N):
J[i1, 2, i1, 2] += A
J[i1, 4, i1, 4] += A
J[i1, 7, i1, 7] += A
J[i1, 2, i1, 4] += A
J[i1, 2, i1, 7] -= 2 * A
J[i1, 4, i1, 7] -= 2 * A
## x_j=8 :x_j=3とx_j=5(ブースR)のOR関数
for i1 in range(N):
J[i1, 3, i1, 3] += A
J[i1, 5, i1, 5] += A
J[i1, 8, i1, 8] += A
J[i1, 3, i1, 5] += A
J[i1, 3, i1, 8] -= 2 * A
J[i1, 5, i1, 8] -= 2 * A
## x_j=9 :x_j=7とx_j=8(ブースLとブースR)のOR関数
J[i1, 7, i1, 7] += A
J[i1, 8, i1, 8] += A
J[i1, 9, i1, 9] += A
J[i1, 7, i1, 8] += A
J[i1, 7, i1, 9] -= 2 * A
J[i1, 8, i1, 9] -= 2 * A
改めて、ルール8の設定をば。
前章でルール8を設定する準備は整いました。
$x_{j=6}$と$x_{j=9}$がどちらも0、或いはどちらも1の場合のみOKということですから、
x_{j=6}-x_{j=9}=0\\
\Leftrightarrow
(x_{j=6}-x_{j=9})^2=0
という式を満たせばよいことになります。コードは下記のようになります。
## 講師と生徒が一方だけいる場合はNG。両方いるか、両方いないときのみOKの関数
## つまり(x_6-x_9)^2 の値が正(1)になるとペナルティ
for i1 in range(N):
J[i1, 6, i1, 6] += A
J[i1, 6, i1, 9] -= 2 * A
J[i1, 9, i1, 9] += A
ルール9: 講師の出勤にはコストがかかる
最後のペナルティです。これはルール1~8のように「絶対に守らなければならない」ルールではないので、定数の値は適当にB=4とでもしておきます。
# ルール9:講師の出勤にはコストがかかる
B = 4 #できれば超えてほしくない値
for i1 in range(N):
for j1 in range(2):
for i2 in range(N):
for j2 in range(2):
J[i1, j1, i2, j2] += B * delta(i1, i2) * delta(j1, j2)
これで制約条件の設定は全て完了です。
計算!
全ての準備は整いました。あとはJをQUBO形式に変換し、wildcatに投げて出力を待ちます。
initial_temperature=500, last_temperature=0.1, scale=0.99
repetition=50
として計算してみました。何回か試して得られた出力がこちら。
Result:
[[1 0 1 0 0 0 1 1 0 1]
[0 0 0 0 0 0 0 0 0 0]
[0 1 0 1 1 0 1 1 1 1]
[0 1 1 0 0 1 1 1 1 1]]
うん、実にそれっぽいです。制約条件をばっちり満たし、かつ不必要に1対1のない理想的な時間割ができています。
太郎君は14時コマに空きができてしまいましたが、こちらは制約条件を増やすことで対応できそうです。
所感
かなり冗長なコードになってしまいましたが、なんとかゴールまでたどり着くことができました。
今回の問題設定を解くにあたって、より最適な記述方式はあるでしょうし、また、そもそものコーディングが間違っている可能性も大いにあります。
その他、「おや?」と疑問が解消できていない部分も多少あります。
また発見があり次第、適宜修正していきます。
今回のコードはこちらにあげておきますので、興味がある方は試してみてください。
https://github.com/papepupi/scheduling-problem/blob/master/1808_scheduling_v1.py