量子アニーリングをする場合、QUBOというものを作って、それをイジング模型に変換することが多いようです。
日本地図を四色に塗り分けるためのQUBOを作って、古典アニーリングをやってみた話をします。
量子アニーリング?
組み合わせ最適化問題を解く確率的アルゴリズムの一種です。
解きたい問題をイジング模型という強磁性体を模したモデルに置き換えて、量子的な効果を含む項を付け加えてコンピュータでシミュレーションすれば、ある種の問題でよい結果が得られる、という論文が昔にあったようです。
これが元々の量子アニーリングです。当時は、量子コンピュータで解くといった話は無く、普通のコンピュータで解くアルゴリズムでした。
ところが、ある日、D-Waveという会社が、実機を使って高速にイジング模型を解く機械を作ってしまいました。
量子アニーリングをする専用機ができてしまったわけですね。
実は、普通に古典コンピュータ(普通のコンピュータ。量子をやってる人は、量子じゃないものを古典といいます)でイジング模型を解いても、割と多くの問題は解けてしまいます。
実際、例えば富士通も従来の半導体技術を使ってイジング模型を解くというようなことをやっています。
実機を使うのは非常にお金がかかりますので、今回はイジング模型を古典アニーリング(量子的な効果を考慮しない、通常の焼きなまし法)で解きます。
古典アニーリングには、次のようなイジング模型の式を使いました。
H = -\sum_{i, j}J_{ij}s_is_j-\sum_i h_is_i
ここで、$s_i$は、電子スピンの向き(上向き or 下向き)を表していて、+1または-1の値を取ります。
この$s_i$をビットに見立てて、Hを最小化する問題を解くことで、組み合わせ最適化問題の解を確率的に得ることができます。
彩色問題?
隣接する都道府県が同じ色にならないように、都道府県を塗ることを考えましょう。
こういった問題をグラフ彩色問題といい、どんな複雑な地図でも、4色あれば塗り分けができることが数学的に証明されています。
地図によっては、4色未満の色数で塗り分けることもできますが、日本地図の場合は4色必要になります。
QUBOを作ろう
いきなり問題をイジング模型に置き換えるのは難しいので、まずはQUBOという問題を作ります。
QUBOとイジング模型は互いに変換できることが分かっているので、QUBOを作ればイジング模型に変換し、実機で量子アニーリングができます。
QUBOは
H=\sum_{i,j}Q_{ij}x_ix_j
のHを最小化する問題で、$x_i$, $x_j$は0か1に対応します。
また、$i<j$にあたる部分は$Q_{ij}=0$となります。
ここで $x_i$ は、都道府県と色の組み合わせを示します。
今回は4色で塗るので、例えば、赤、黄、青、橙としましょう。
| $x_i$ | 都道府県 | 色 |
|---|---|---|
| $x_0$ | 北海道 | 赤 |
| $x_1$ | 北海道 | 黄 |
| ... | ... | ... |
| $x_{4a+b}$ | 都道府県a | 色b |
| ... | ... | ... |
| $x_{187}$ | 沖縄県 | 橙 |
のように$x_i$を割り当てます。
そして $x_0 = 1$ は、北海道を赤で塗ること、 $x_0 = 0$ は、北海道を赤で塗らないことを表すことにします。
続いて、望ましい状態でHが最小になるよう、Qの係数を設定していきます。
まず、各都道府県が、ちょうど1色のみで塗られている状態が望ましいです。
つまり、北海道が赤かつ黄とか、沖縄県が色なし、というのは避けたいということです。
for pr in range(N_PREF): # N_PREF=47 (都道府県数)
for c1 in range(N_COLOR): # N_COLOR=4 (色数)
Q[pr*N_COLOR + c1, pr*N_COLOR + c1] = -1.0
for c2 in range(c1+1, N_COLOR):
Q[pr*N_COLOR + c1, pr*N_COLOR+c2] = 1.0
こんな感じになります。
Q =
\begin{bmatrix}
-1&1&1&1&&&&&\cdots\\
0&-1&1&1&&&&&\cdots\\
0&0&-1&1&&&&&\cdots\\
0&0&0&-1&&&&&\cdots\\
&&&&-1&1&1&1&\cdots\\
&&&&0&-1&1&1&\cdots\\
&&&&0&0&-1&1&\cdots\\
&&&&0&0&0&-1&\cdots\\
\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\ddots
\end{bmatrix}
QUBO問題は、$H=\Sigma_{i,j}Q_{ij}x_ix_j$ を最小化する、という問題でした。
同じ都道府県内に、複数の色が塗られていた場合、つまり $x_i=1, x_j=1$ ($i\ne j$, $x_i$と$x_j$は同都道府県)のとき、 $Q_{ij}=1$なので、$Q_{ij}x_ix_j = 1$ となり、Hが大きくなります。
一方で、何か1色だけ塗っておけば $Q_{ii}x_ix_i = -1$となり、Hが小さくなります。
続いて、隣接している都道府県は同じ色で塗らない、という制約を入れます。
隣接する都道府県は、neighborという辞書に
{pref_id['青森県']: [pref_id['北海道'], pref_id['岩手県'], pref_id['秋田県']]}
のような形で入っているとします。ただし、pref_idは各都道府県を連番の数値に表したもので、i = pref_id['青森県']とおくと、$x_{4i}, x_{4i+1}, x_{4i+2}, x_{4i+3}$が、それぞれ、青森県の赤、黄、青、橙に対応する、と考えてください。
for k, ne in neighbor.items():
for kk in (x for x in ne):
# k, kkは互いに隣接する都道府県。
if k > kk:
# QUBOマトリックスはi<jではQij = 0のため。
continue
for c in range(N_COLOR):
Q[k*N_COLOR + c, kk*N_COLOR + c] = 1.0
Q =
\begin{bmatrix}
\ddots&\vdots&\vdots&\vdots&\vdots\\
\cdots&1&0&0&0&\cdots\\
\cdots&0&1&0&0&\cdots\\
\cdots&0&0&1&0&\cdots\\
\cdots&0&0&0&1&\cdots\\
&\vdots&\vdots&\vdots&\vdots&\ddots
\end{bmatrix}
隣接する都道府県のところの行列は、上のようにします。こうすると、同じ色に塗った場合にHが大きくなります。
これでQUBOマトリックスは完成です。
あとはイジング模型に直して、解くだけです。
やってみた
h = [-sum(Q.get((i, k), 0.0) + Q.get((k, i), 0.0) for k in range(N)) for i in range(N)]
J = {k: -v for k,v in Q.items() if k[0] < k[1]}
イジング模型への変換は、これでできるらしいです。
また、古典アニーリングのソースは、昨日のアドベントカレンダーの記事を書かれたMDRさんのgithubを参考にさせていただきました。
s = [random.choice((-1.0, 1.0)) for _ in range(N)]
kt = 5.0
e = -sum(J[i,j] * s[i] * s[j] for i,j in J) - sum(h_ * s_ for h_, s_ in zip(h, s))
for _ in range(10000):
# ひっくり返すスピンを選択
t = random.randrange(N)
# ひっくり返したときのエネルギーの変化を計算
delta_e = sum(J[i,j] * s[i] * s[j] for i,j in J if i == t or j == t) + h[t]*s[t]
delta_e *= 2.0
if delta_e < 0 or math.exp(-delta_e/kt) > random.random():
e += delta_e
s[t] = -s[t]
kt *= 0.99
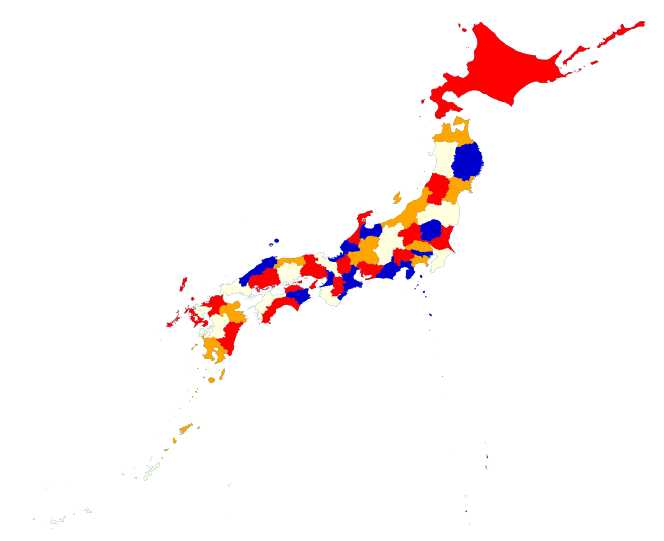
結果、こうなりました。
なんとなくいい感じに色分けされてますね!
こちらに、今回やってみたノートブックを置いてます。
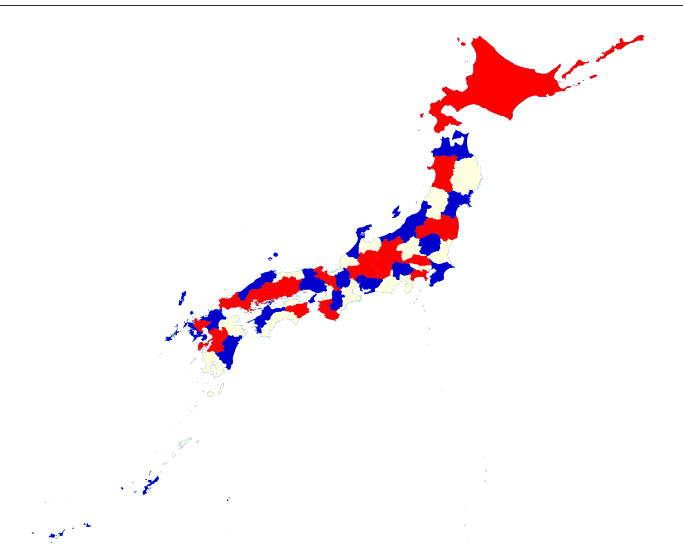
おまけ1: 3色だったらどうなるの?
一部は同じ色で塗られているところがありますが、大体合ってる感じです。
3色で塗るのは不可能なので、人間が手でやっても、似たようなことになると思われます。
おまけ2: 日本地図の描き方
geopandasというライブラリと https://github.com/dataofjapan/land のデータを使ったら簡単にできました。