初投稿失礼いたします。
決勝進出者も決まり、今年のM1もいよいよ残るは決勝戦です。
個人的にはパンプキンポテトフライの準々決勝が面白かったですが落ちてしまいましたね、、、
私はしがないエンジニアですが、最近データ分析にハマっております。
ということで、データ分析の練習も兼ねて、M1をデータ分析して予想してみましょう!
今回はgoogle colaboratory(python)を用いて分析します。
現在、競馬予想モデルで予想ブログ運営しております。最新の予想はこちらから。
タスクの確認と仮説
今回は 合計得点 を予測しましょう。回帰タスクってやつですね。
分析するにあたって、まずは仮説を立ててみましょう。
簡単に思いつくものだと、やはり出番順は点数に大きく影響しそうですね。(残念ながら出番順は笑みくじなので予想には使えませんが、、、)
あと思いつくのは、 結成年、 決勝出場経験、 所属事務所 あたりでしょうか。
とりあえずこの辺りに目星をつけてデータを用意しましょう!
どの程度データを用意しようか悩みましたが、2017年のとろサーモン優勝の年から今と同じような7人態勢の採点方式になったみたいですね。今回は2017~2022年までの6年分のデータを用意します。
データはwikiからスクレイピングして、以下の値を集めます。
・合計点
・各審査員の採点結果
・結成年
・決勝出場回数
・出番順
※後々ABCお笑いグランプリの結果もファクターに追加しました
データとして合計得点だけでなく、審査員それぞれの点数も用意する予定なので、まっちゃんの採点結果も予想できそうですね。
データの前処理
前述の通り、今回はwikiからデータをスクレイピングします。
wikiでは出場コンビの情報と、各審査員の採点結果の2つにテーブルが分かれています。いったんそれぞれのテーブルをスクレイピングしてdataframeに格納します。
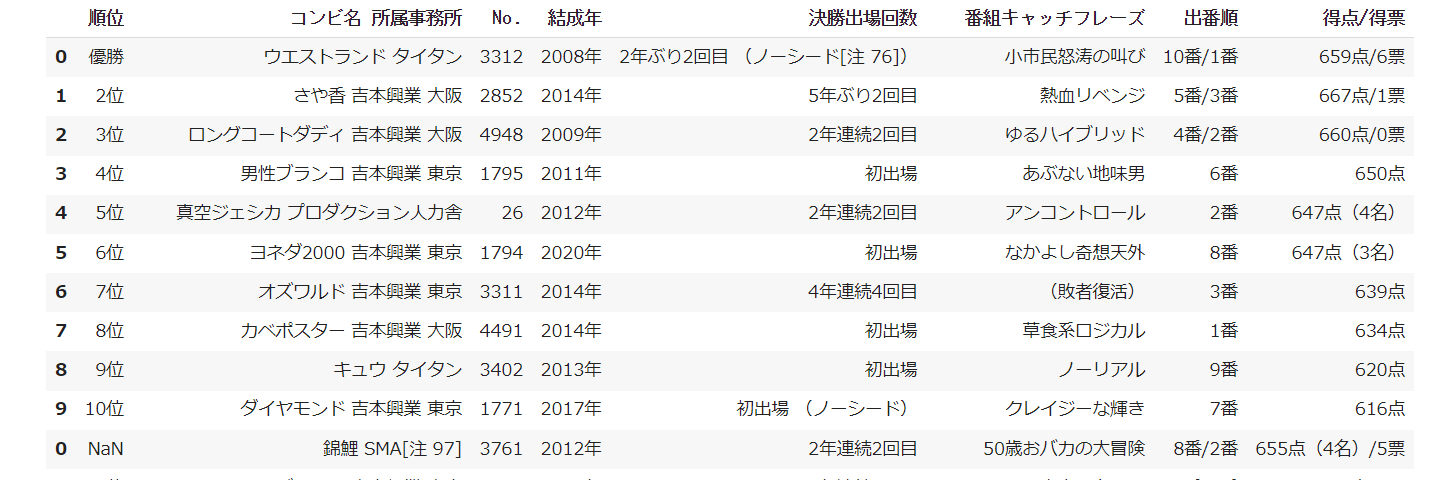
出場コンビの情報
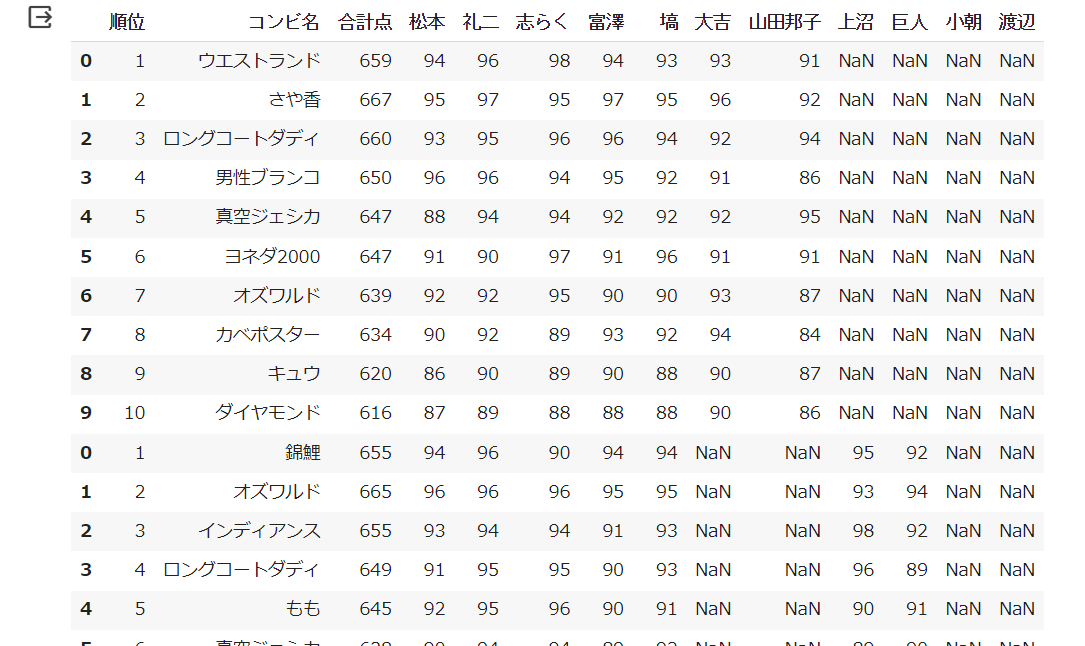
各審査員の採点結果テーブル
こんな感じでデータは取得できました。各審査員の採点結果テーブルの方は特に前処理しなくてもこれでデータは使えそうです。出場コンビの情報テーブルの方はいらないデータの削除などいろいろテコ入れしてやりましょう。
・不要なカラムの削除(順位、No.、キャッチフレーズ、得点)
・所属事務所→吉本か否かで分類(吉本:0 非吉本:1)
・結成年→コンビ歴に変更(開催年ー結成年の値)
・決勝出場回数→初出場か連続出場か〇年ぶりかで分類(初:0 連続:1 ぶり:2)
・出番順を文字列→数値データに変更
上記リストのように前処理行いました。順に解説します。
不要なカラムの削除(順位、No.、キャッチフレーズ、得点)
順位、得点については他テーブルにあるので消しちゃいましょう。
No.(エントリーナンバー)とキャッチフレーズについても今回扱うのは諦めました。
余談ですが、令和ロマンのyoutubeをみていると、どうやら所属事務所などによってまとめてエントリーしているようですね。決勝を分析するのには微妙ですが、二回戦に進めるかの予想などにはもしかしたら使えるのかもしれませんね。
所属事務所→吉本か否かで分類(吉本:0 非吉本:1)
なんとなく吉本ってやっぱ点数高いんじゃねっていう仮説からここは吉本か否かで分類わけしました。
文字列に 吉本 が含まれるかで判別しました。
konbi3["コンビ名 所属事務所"][konbi3["コンビ名 所属事務所"].str.contains('吉本') == True] = 0
konbi3["コンビ名 所属事務所"][konbi3["コンビ名 所属事務所"].str.contains('吉本') == False] = 1
コンビ歴に変更(開催年ー結成年の値)
M1は復活してからコンビ歴15年まで参加可能となっていますね。
こちらは結成年だと現状文字列ですし、扱いにくいためコンビ歴に変えましょう。
まずは文字列を数値に変更し、開催年から結成年を引いた値を格納していきます。
#文字列を数値に変更
konbi3["結成年"]=konbi3["結成年"].str[:4].astype(int)
#コンビ歴に変更
i=0
k=0
while(i<60) :
konbi3.loc[i,"結成年"]=2022-k-konbi3.loc[i,"結成年"]
i+=1
if(i%10==0):
k+=1
決勝出場回数→初出場か連続出場か〇年ぶりかで分類(初:0 連続:1 ぶり:2)
ここの処理は結構悩みました。出場回数でわけるかどうするか。
シンプルに初出場か否かでデータを分けようかとも考えましたが、スーマラのyoutubeで武智さんが「久しぶりの出場だとネタもたまってるから強いよな」的なことを言っていました。
今回は初出場、連続出場、久々の出場の3つに分類します。
文字列に 初出場 、 連続 、 ぶり が含まれるかで判別しました。
konbi3["決勝出場回数"][konbi3["決勝出場回数"].str.contains('初出場') == True] = 0
konbi3["決勝出場回数"][konbi3["決勝出場回数"].str.contains('連続') == True] = 1
konbi3["決勝出場回数"][konbi3["決勝出場回数"].str.contains('ぶり') == True] = 2
出番順を文字列→数値データに変更
ここは文字列を数値に変更するだけですね。
あまりいい方法が思いつかなかったので力技で変換しました。
konbi3["出番順"][konbi3["出番順"].str[:2] == "1番" ] = 1
konbi3["出番順"][konbi3["出番順"].str[:2] == "2番" ] = 2
konbi3["出番順"][konbi3["出番順"].str[:2] == "3番" ] = 3
konbi3["出番順"][konbi3["出番順"].str[:2] == "4番" ] = 4
konbi3["出番順"][konbi3["出番順"].str[:2] == "5番" ] = 5
konbi3["出番順"][konbi3["出番順"].str[:2] == "6番" ] = 6
konbi3["出番順"][konbi3["出番順"].str[:2] == "7番" ] = 7
konbi3["出番順"][konbi3["出番順"].str[:2] == "8番" ] = 8
konbi3["出番順"][konbi3["出番順"].str[:2] == "9番" ] = 9
konbi3["出番順"][konbi3["出番順"].str[:2] == "10" ] = 10
これで成型できましたね。あとは2つのテーブルをくっつけて完成です。
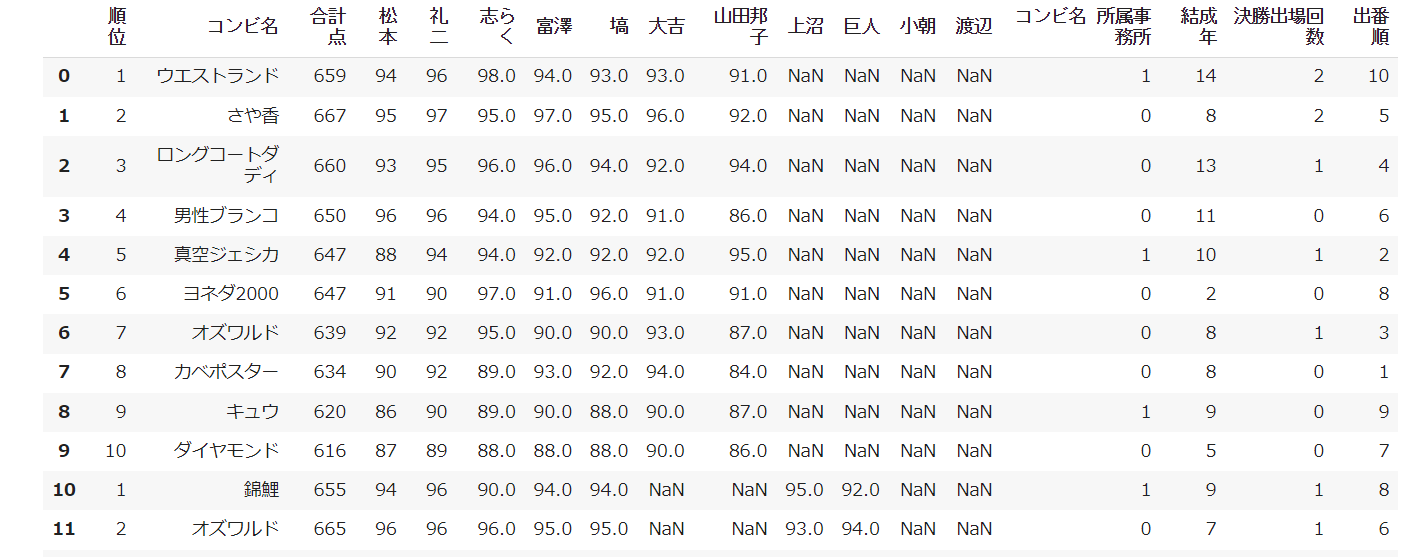
作成したデータがこちらになります。
作成データ
ようやく前処理終わりです。
ここがデータ分析の肝でもありますし、時間のかかるところですね、、
スクレイピングの知識も乏しい私にとってはなかなかハードでした。
各要素と合計点の関係を確認
さて、いよいよ予測モデル作成!と言いたいところですが、いったんデータの可視化を行い、データを分析していきましょう。
所属事務所と合計点の関係
所属事務所については吉本か否かで分けていましたね。
それぞれの所属コンビの合計点の平均値を求めます。
分析結果以下になります。
#カラム名をyosimotoに変更
print("吉本: %.2f"%(m1_1[m1_1.yosimoto == 0].合計点.mean()))
print("非吉本: %.2f"%(m1_1[m1_1.yosimoto == 1].合計点.mean()))
吉本: 644.82
非吉本: 634.47
10点の差が出ました。やはり天下の吉本なんですかね。
個人の感想ですが、吉本以外のコンビは色物が多いイメージもありますね。(主にランジャタイのイメージですが笑)
吉本以外のコンビも活躍しているイメージはありますが、イマイチ点数が伸びなかったコンビも非吉本であることが多いみたいですね。
コンビ歴と合計点の関係
直観だとやはりコンビ歴の長い方が成績もよくなりそうですよね。
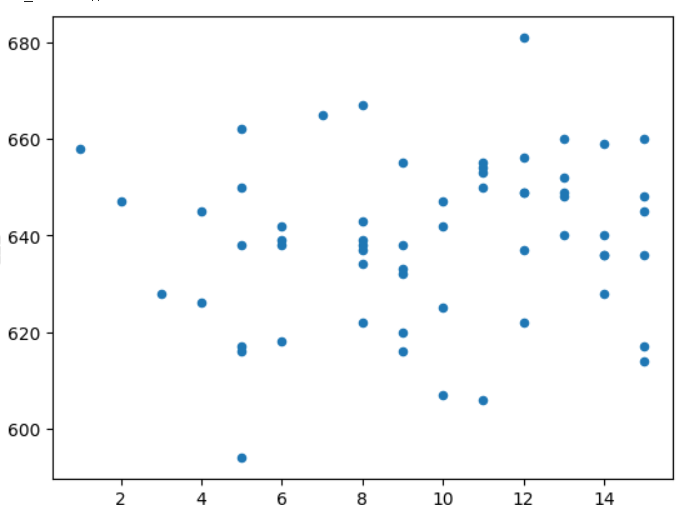
実際のところコンビ歴と合計点に因果関係は生まれるでしょうか。
散布図をみると、、、あまり関係なさそうですね。
相関係数も求めてみると、0.12でした。
思っているよりも若いコンビも活躍しているみたいですね。
これは予想モデル作成時にファクターとして用いるか要検討ですね。
決勝出場経験と合計点の関係
こちらは初出場、連続出場、〇年ぶりかで分類していましたね。
初出場よりは複数回決勝に進んでいるコンビの方が強そうですがどうでしょうか。
print("初出場: %.2f"%(konbi3[konbi3.決勝出場回数 == 0].合計点.mean()))
print("連続: %.2f"%(konbi3[konbi3.決勝出場回数 == 1].合計点.mean()))
print("ぶり: %.2f"%(konbi3[konbi3.決勝出場回数 == 2].合計点.mean()))
初出場: 635.87
連続: 642.68
ぶり: 643.86
これは予想通りでしたね。初出場か否かで7点程度差が出ました。
連続出場と〇年ぶり出場では大きな差は出ませんでしたが、一応〇年ぶり出場の方が1点高いです。やはり武智さんの言う通り、ネタを温存して挑めるのが強いんでしょうか。
出番順と合計点の関係(おまけ)
出番順は笑みくじなので予想ファクターに含めることは出来ませんが、せっかくなので覗いてみましょう。
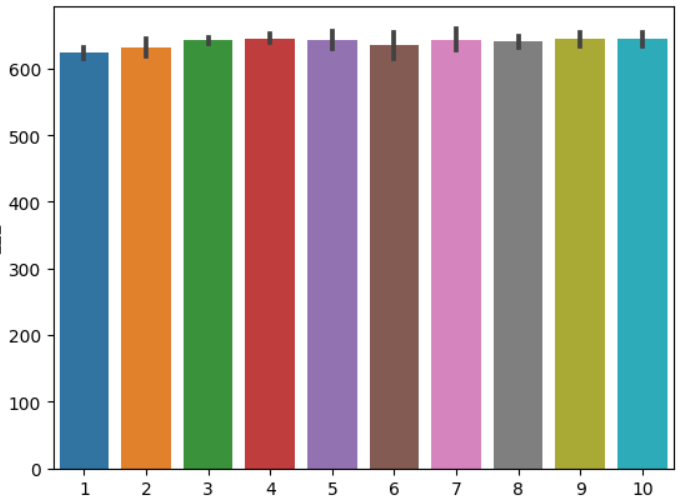
まずは各出番順の平均点です。
sns.barplot(x="出番順", y="合計点", data=m1_1)
for i in range(10):
print(str(i+1)+"番目: %.2f"%(m1_1[m1_1.出番順 == i+1].合計点.mean()))
1番目: 624.00
2番目: 631.17
3番目: 642.00
4番目: 644.83
5番目: 642.67
6番目: 635.67
7番目: 642.33
8番目: 640.83
9番目: 644.17
10番目: 645.33
こう見ると1番目は厳しいのはもちろん、2番目もかなり苦しいようですね。
逆に3番目は他とも見劣りしない点数です。
3番目の出番にはもう会場もあったまって点数も伸びるみたいですね。
応援しているコンビが1,2番を引かないことを祈りましょう。
予測モデル作成
いよいよモデル作成です。
今回は 決定木 を用いてモデルを作成します。
まずは説明変数に"所属事務所", "結成年", "決勝出場経験"を用いて作成してみます。
# 目的変数と説明変数の値を取得
target = konbi3["合計点"].values
features_one = konbi3[["コンビ名 所属事務所", "結成年", "決勝出場回数"]].values
# 決定木の作成
my_tree_one = tree.DecisionTreeClassifier()
my_tree_one = my_tree_one.fit(features_one, target)
これだけで予測モデルができてしまいました。
機械学習・AIでPythonが使われる理由がよくわかりますね。
あとは予測させてみましょう。
# 説明変数の値を取得
test_features = m2023[["コンビ名 所属事務所", "結成年", "決勝出場回数"]].values
# 予測
my_prediction = my_tree_one.predict(test_features)
結果がこちらです。
1位:655点:さや香
1位:655点:カベポスター
3位:653点:真空ジェシカ
4位:649点:ダンビラムーチョ
4位:649点:マユリカ
6位:636点:モグライダー
7位:622点:ヤーレンズ
8位:616点:令和ロマン
8位:616点:くらげ
結構ありえそうな結果、、、なんですかね笑
わたしは決勝までそのコンビのネタは極力見ないようにして本番楽しむタイプなので、準決勝イチウケとも噂のあるモグライダーも最近のネタ知りません!
上位3組は優勝候補筆頭のさや香も含めていい線予想している気がしますね。
ただ、説明変数が少ないため、[さや香、カベポスター]、[ダンビラムーチョ、マユリカ]、[令和ロマン、くらげ]のデータが被ってしまいました。(にしてもここまで被るのも珍しい気がしますね、、)
まとめ
ひとまずこのモデルではさや香、カベポスター、真空ジェシカの3組が決勝ラウンド進出予想ですね!
さて、この結果を受けてもう少し改良したくなりました。もっと説明変数を増やしたいですよね。
そこで、ABCお笑いグランプリでの成績の情報の追加を思いつきました。
次回はさらに情報を付け加えてM1の予想をしてみたいと思います!
最後までご覧いただきありがとうございます!!現在、競馬予想モデルで予想ブログ運営しております。最新の予想はこちらから。