対象
- 機械学習を始め、Deep Learningを始めたい方
- Deep Learning の実装方法(ライブラリ)を探っている方
- tensorflow、kerasの使い方を知りたい方
-前提知識:Python、numpyの基本的な知識を持っている方。
はじめに
いくつかのDeep Learning技術の応用研究を行っているのですが、使用しているライブラリを構築している、
tensorflow、kerasの使い方を恥ずかしながら殆ど知らなかったので、一般的なロジスティック回帰を実装することで、大まかな使い方を勉強してみたので共有させていただきます。
今回は、理論、コード面共に、巣籠 悠輔さんの書かれた以下の書籍を参考にさせていただきました。ありがとうございます。
https://www.amazon.co.jp/dp/B072JC21DH/ref=dp-kindle-redirect?_encoding=UTF8&btkr=1
パーセプトロンを用いたロジスティック回帰
- 単純パーセプトロン
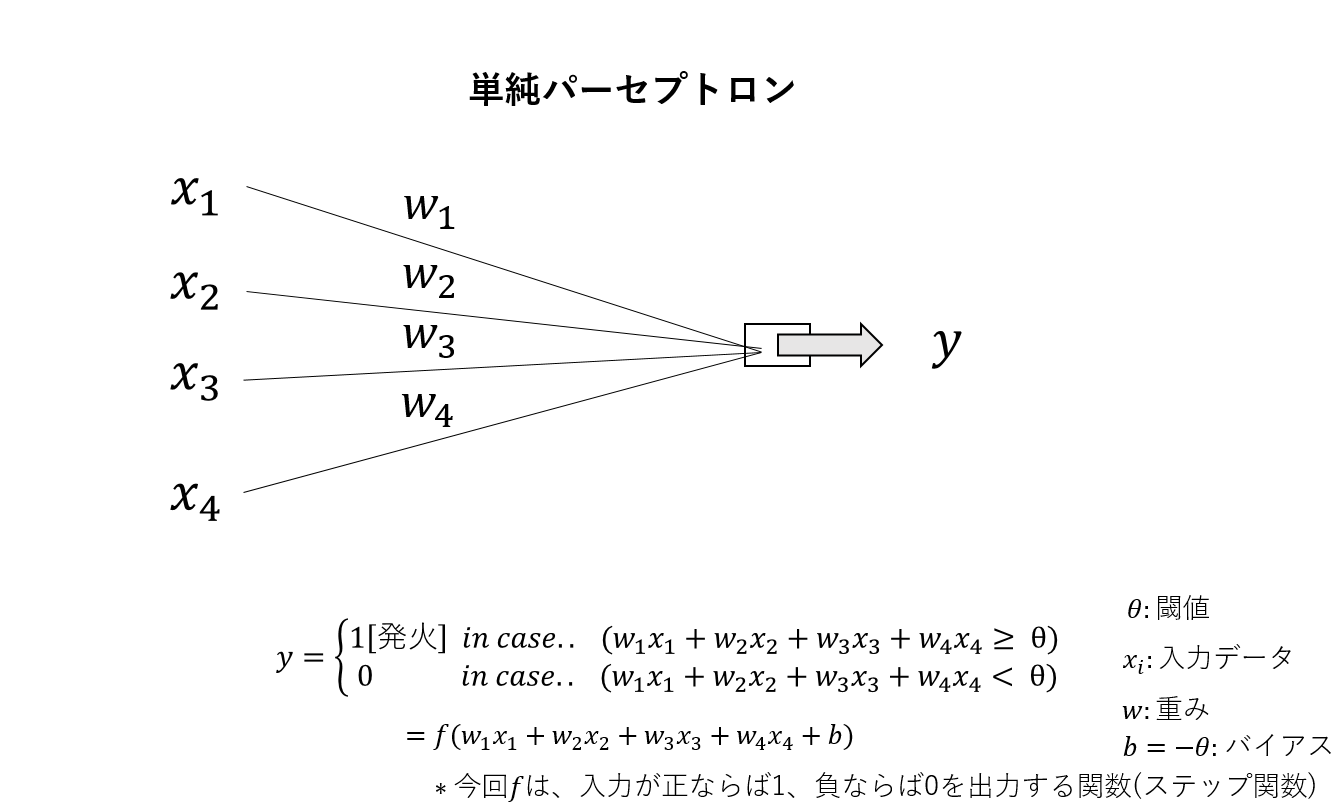
単純パーセプトロンとは、DeepLearningを含むニューラルネットワークの中でも最も簡単なもので、入力データであるxの1次結合で表された式を、活性化関数とよばれる関数fを用いて変換した式として定義されます。また、以下のwはxの各成分の重みと呼び、bをバイアスと呼びます。
f(X) = \left\{
\begin{array}{ll}
1 & (X \geq 0) \\
0 & (X \lt 0)
\end{array}
\right.
X = \sum w_ix_i + b
ここで、パーセプトロンの中でも単純パーセプトロンとは、活性化関数fを、ステップ関数を用いて表したもののことを言います。これは、入力Xが正ならば1を、負ならば0を出力する関数です。
- ロジスティック回帰
単純パーセプトロンでは、活性化関数にステップ関数を用いましたが、このステップ関数の代わりに、以下の
シグモイド関数σ(0~1が出力される)を用いたものをロジスティック回帰といいます。
y = \sigma(\sum w_i x_i + b) \\
\sigma = \frac{1}{1+e^{-X}} \\
X = \sum w_ix_i + b
このシグモイド関数により、出力は0、1の二択ではなく(ニューロンが発火するか、しないかの二択)、
0~1となり、発火を確率的にコントロールすることになります。確率的にコントロールすることで、
入力が発火するか、しないかの微妙な部分を認識することにつながります。
学習における準備(tensorflow、keras共通)
- 学習データ
今回の学習では、2進数で0~7を表した8つのデータ[[0,0,0]~[1,1,1]]を用いました。
教師ラベルは、各リスト内(入力)で0が多いときは0を出力し、1が多いときは1を出力します。
例:[0,0,1]→0、[1,0,1]→1
- 誤差関数
ロジスティック回帰に限らず、一般に機械学習では、誤差関数というものを定義し、それを最小化
しようとすることで学習を行います。
この誤差関数は、解きたい問題に応じて最大化すべき尤度関数を、少しいじることで得られたものです。
一般に尤度関数Lは以下の式で表現されます。
L(w,b) = \prod_{i=0}^N p(C = t_i | x_i) \\
= \prod_{i=0}^N \sigma(w^Tx_i + b) \times (~(1-\sigma(w^T x_i + b) ~ ) \\
x_i: i番目の入力データ, ~~
t_i: i番目のラベル, ~~
N:入力データ数 \\ \\
\prod_{i=0}^N \sigma(w^Tx_i + b) : 発火する(出力が1になる)確率 \\
\prod_{i=0}^N \sigma(w^Tx_i + b) \times (~(1-\sigma(w^T x_i + b) ~ ):発火しない(出力が0になる)確率
尤度関数についての詳しい説明はここでは省略させていただきます。詳しくは、以下などをご参照ください。
上記の尤度関数の符号を反転し、対数を取ることで、交差エントロピー関数という誤差関数を得ます。
今回は、この交差エントロピー関数E2を最小化することで学習を行います。
一般的に機械学習では、最大化問題を解くのではなく、最小化問題を解くことが殆どです。
E2(w,b) = -logL(w,b) \\
- 学習方法
誤差関数を用いて特徴量空間を探索することで学習を行いますが、探索の仕方について見ていきます。
今回は、SGD、確率的勾配降下法と呼ばれる手法を用いて学習を行います。
この手法の基礎となる手法として勾配降下法(GD)があります。
これは、誤差関数Eをパラメータであるw,bでそれぞれ偏微分して得られた値を用いてパラメータの更新を以下の様に行います。
(式変形の説明は省きます。すみません。)
w^{k+1} = w^k - \eta \frac{\sigma E(w,b)}{\sigma w} \\
= w^k + \eta \sum_{i=1}^N (t_i - y_i)x_i ~~,\\
\\ \\
b^{k+1} = b^k - \eta \frac{\sigma E(w,b)}{\sigma b} \\
= b^k + \eta \sum_{i=1}^N (t_i - y_i)x_i \\
\\
\eta:学習率, x_n:i番目の入力データ, t_i:i番目のラベル, y_i:i番目のネットワーク出力(0~1)
この勾配降下では、N個全てのデータを用いてパラメータ更新(学習)を行いますが、
確率的勾配降下法では、N個のデータからランダムに選ばれた1つのデータを用いて順次パラメータ更新を行います。これにより、より計算コスト等の面で効率的な学習を狙うことができます。
Tensorflowでの実装
以上を踏まえて、実装方法を確認していきましょう。
まずはtensorflowでの実装です。
tensorflowでは、パラメータ等を入れる変数(Variable)、データ等を入れる箱(placeholder)を定義する必要がある他、
誤差関数を手入力で実装しなければいけない分、kerasに比べるとやや面倒に感じましたが、
より機械学習の仕組みを知りながら実装できるのは良いと感じました。(小並感)
全体のコードは以下となります。
import numpy as np
import tensorflow as tf
# 変数定義
w = tf.Variable(tf.zeros([3,1]))
b = tf.Variable(tf.zeros([1]))
# 入れ物 プレースホルダー定義
x = tf.placeholder(tf.float32, shape=[None, 3]) #入力
t = tf.placeholder(tf.float32, shape=[None, 1]) #ラベル
y = tf.nn.sigmoid(tf.matmul(x,w) + b) #ネットワークの出力(ラベルではない)
# 誤差関数(今回は交差エントロピー関数)
cross_entropy = -tf.reduce_sum(t * tf.log(y) + (1-t) * tf.log(1 - y))
# 訓練方法定義(今回は 確率的勾配降下法を、学習率0.1で行う)
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cross_entropy)
correct_prediction = tf.equal(tf.to_float(tf.greater(y, 0.5)), t)
# 学習データ定義
X = np.array([[0,0,0],[0,0,1],[0,1,0],[0,1,1],[1,0,0],[1,0,1],[1,1,0],[1,1,1]])
Y = np.array([[0],[0],[0],[1],[0],[1],[1],[1]])
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
# エポック数200で学習を行う
# 学習方法はtrain_stepで定義されたものを用いる。
# feed_dictを書くことで、さっき定義した学習データをネットワークにセットする
for epoch in range(200):
sess.run(train_step,feed_dict={
x:X,
t:Y
})
# 学習結果確認
classified = correct_prediction.eval(session=sess,feed_dict={
x:X,
t:Y
})
print("学習結果:\n",classified)
# 入力に対する出力確率
prob = y.eval(session=sess, feed_dict={
x:X,
t:Y
})
print("prob:\n",prob)
# 最終的なパラメータ(w,b)確認
print("w:",sess.run(w))
print()
print("b:",sess.run(b))
- 出力
学習結果:
[[ True]
[ True]
[ True]
[ True]
[ True]
[ True]
[ True]
[ True]]
prob:
[[0.00520364]
[0.16293728]
[0.16293728]
[0.87869316]
[0.16293728]
[0.87869316]
[0.87869316]
[0.9963038 ]]
w: [[3.6166463]
[3.6166463]
[3.6166463]]
b: [-5.25318]
注意点としては、以下の3つがあります。
① placeholder[None,2]のように、第一引数にNoneを入れることで、データ数指定をしなくてよいこと
②学習の前に
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
としてモデルの初期化を行うこと
③w,bなど変数(Variable)の出力を行う際はsess.run(Variable)とすることで行う
です。
以上となります。
kerasでの実装
kerasでの実装は、tensorflowのそれに比べ、遥かに直感的だと感じました。
具体的には、パラメータの定義も必要なく、ネットワーク構造を数行で書けてしまいます。
個人的には、sklearnの様に、numpy配列をそのまま学習に用いることができる点に良さを感じました( ´∀` )
全体のコードは以下の様になります。
# 必要ライブラリインポート
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD
"""
モデル設定
"""
model = Sequential([
Dense(input_dim = 3, units=1),
Activation("sigmoid")
])
# 誤差関数、最適化手法、学習率の定義
model.compile(loss="binary_crossentropy", optimizer=SGD(lr=0.1))
"""
モデル学習
"""
# 0が多ければ0を、1が多ければ1を出力する
X = np.array([[0,0,0],[0,0,1],[0,1,0],[0,1,1],[1,0,0],[1,0,1],[1,1,0],[1,1,1]])
Y = np.array([[0],[0],[0],[1],[0],[1],[1],[1]])
# エポック数(学習の繰返し数)、バッチサイズ(一回のパラメータ更新にいくつのデータを用いるか)を指定
# 学習
model.fit(X,Y, epochs=200, batch_size=1)
"""
学習結果確認
"""
classes = model.predict_classes(X, batch_size=1)
prob = model.predict_proba(X, batch_size=1)
print("classified:")
print(Y==classes,"\n")
print("output probability:")
print(prob)
- 出力(中略)
Epoch 199/200
8/8 [==============================] - 0s 749us/step - loss: 0.1172
Epoch 200/200
8/8 [==============================] - 0s 1ms/step - loss: 0.1167
classified:
[[ True]
[ True]
[ True]
[ True]
[ True]
[ True]
[ True]
[ True]]
output probability:
[[0.00497103]
[0.16053352]
[0.16062692]
[0.87988156]
[0.16078575]
[0.880006 ]
[0.88007915]
[0.9964528 ]]
直感的な為、コードもわかりやすいと思います(わかりにくければすみません)。
ネットワーク構造、活性化関数を含むモデル設定、および誤差関数定義を行い、学習を行います。
出力では、学習したネットワークに再度元の入力データを入れ(ふつうはだめです)、正しく学習できている(True)ことを
確認するとともに、各入力に対する尤度関数の値を出力しています。この値が大きいほど、出力を1だと予測し、
小さいほど、0だと予測していることになります。
前述した学習データの定義より、概ね正しく学習できている(1が多い入力データは少なくとも0.5よりは上の値を取っている、反対に0が多い入力データは0.5より小さい値をとっている。)ことがわかります。
さいごに
簡単な実装であればkerasでいいかもと思いました。(ダイエットがんばります)