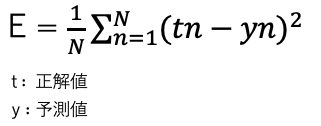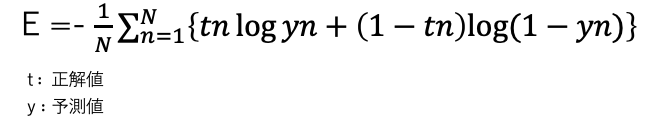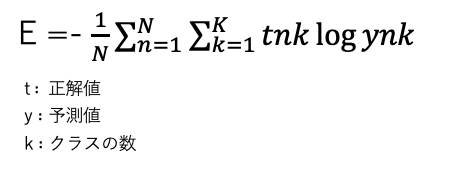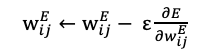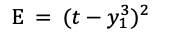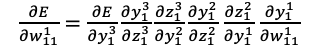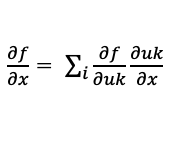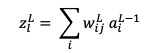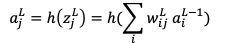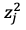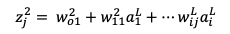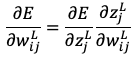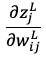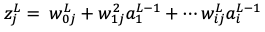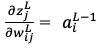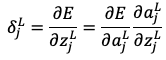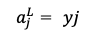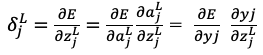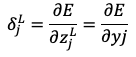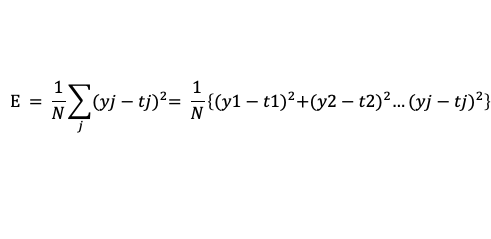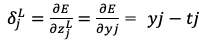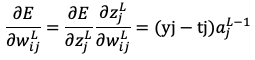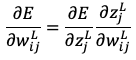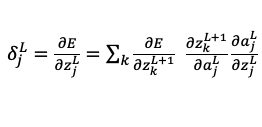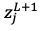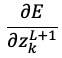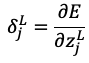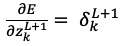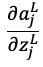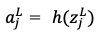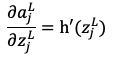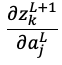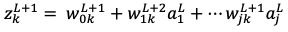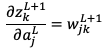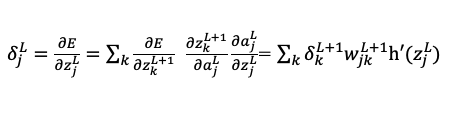前回、ニューラルネットワークをざっくりと理解する パーセプトロン、活性化関数編でパーセプトロン、活性化関数についてざっくりと解説しました。今回では損失関数、誤差逆伝播法(バックプロパゲーション)について紹介していきます。
学習とは
そもそも学習するとは、予測と正解ラベルが最大限に一致するように重みパラメータを最適に調整することです。では最適とはどのように判断するのでしょうか。
- モデルの当てはまりの良さを考える
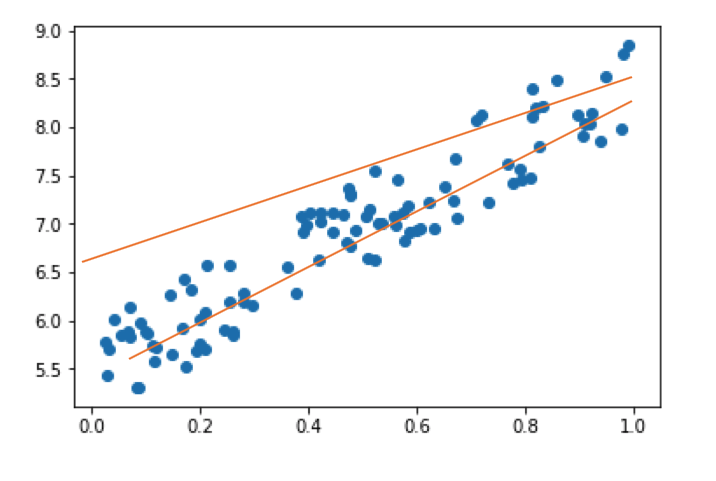
上のグラフの二本の線はどちらの当てはまりが良いでしょうか?
下の線の当てはまりが良さそうですが、この当てはまりを定量的に計る必要があります。
損失関数
予測値と正解値にどれくらいの誤差(損失)があるのかを示す関数で、誤差(損失)とはモデルの当てはまり(精度)の悪さを示している。
つまり、誤差(損失)が小さいほど、そのモデルは優秀であるといえます。この誤差(損失)が最小になっている状態を最適と言い学習の目標は、この損失関数を最小化(最適化)することです。
損失関数の種類
扱うデータ、モデル、分析の目的に応じて正しく損失関数を定義する。
- 回帰問題:二乗誤差
二乗誤差を最小化するように重みパラメータを決定する手法を最小二乗法と呼びます。数式は以下の通りです。
- 分類問題:交差エントロピー
尤度関数というモデルの当てはまりの良さを示す関数の負の対数を撮ったもの。予測値と正解値が一致していると0になります。数式は以下の通りです。
多値分類の具体例:
2つのモデルを使ってある人の服のサイズ(S,M,L)を予測したい。
出力はそれぞれ以下のようになった。なお正解ラベルはMです。
y = (S, M, L)
1, y=(0.01, 0.98, 0.01)
2, y=(0.25, 0.60, 0.15)
それぞれの交差エントロピーを計算すると
1, y = -(0 * log0.01 + 1 * log0.98 + 0 * log0.01)=-{0 + (-0.02) + 0} = 0.02
2, y = -(0 * log0.25 + 1 * log0.60 + 0 * log0.15)=-{0 + (-0.51) + 0} = 0.51
となり、1番の出力の誤差の方が小さいため最適であると言えます。
損失関数の最小化方法と種類
一般に、ある関数の最小値を求めたいというときは、それぞれの変数について偏微分したものを0と置いて連立方程式を解く。偏微分によって得られた関数は接戦の傾きを表しており、最小値では接戦の傾きが0になるため=0とおけます。
- 勾配降下法
・重みパラメータを少しずつ更新していって最適値を探す方法。
・損失関数を重みパラメータで偏微分すると、接戦の傾きを求めることができる。またどちらの方向に重みを変化させると損失が減少するかがわかります。
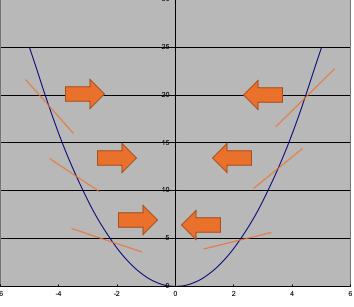
※矢印は更新方向
接戦の傾きがマイナスなら重みを増加し、接戦の傾きがプラスなら減少させると最小値に近づく。
更新式は以下の通りになります。
- ミニバッチ勾配降下法
膨大なデータを取り扱うことが多い近年、そうなるとすべてのデータについての誤差を計算することが計算コストの観点から難しく、また非効率です。ミニバッチ勾配降下法はランダムにいくつかのデータ集合(ミニバッチ)を使って、実際には勾配降下法を適応します。
ミニバッチの大きさはデータによって変わるが、32,64,128,256など2の累乗が使われることが多い。
では実際に勾配降下法をニューラルネットワーク(多層パーセプトロン)に適用させてみる。
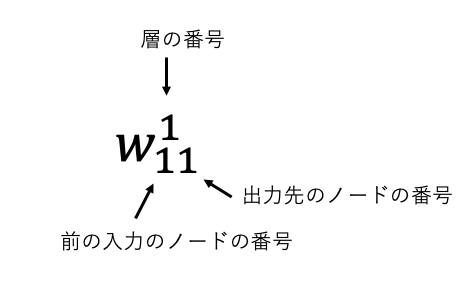
なお重みパラメータは次のように見ます。
最終的な予測値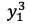 と
と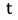 (正解ラベル)の二乗誤差を考えると以下のようになります。
(正解ラベル)の二乗誤差を考えると以下のようになります。
この損失関数をそれぞれの重みパラメータで偏微分した形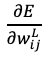 を求める。今回は例として
を求める。今回は例として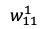 で偏微分してみます。
で偏微分してみます。
この数式は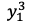 という予測値に対して一番はじめの重みパラーメータ
という予測値に対して一番はじめの重みパラーメータ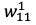 をどれだけ変化させるのかという式です。一つの重みパラメータを求めるだけで一苦労ですが、すべての重みパラメータについて、さらにデータN個分計算することになります。つまり偏微分の具体的な結果を求めることが困難であるため、偏微分の結果をもっと簡単に得る工夫が必要となります。
をどれだけ変化させるのかという式です。一つの重みパラメータを求めるだけで一苦労ですが、すべての重みパラメータについて、さらにデータN個分計算することになります。つまり偏微分の具体的な結果を求めることが困難であるため、偏微分の結果をもっと簡単に得る工夫が必要となります。
誤差逆伝播法(バックプロバゲーション)
誤差逆伝播法(バックプロバゲーション)の前に微分の連鎖律について解説しておきます。
微分の連鎖律
今回の目標は、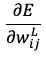 を簡単に求めることですが、そこで微分の連鎖律を使います。
を簡単に求めることですが、そこで微分の連鎖律を使います。
微分の連鎖律とは、関数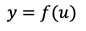 と
と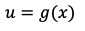 がある時、
がある時、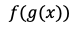 の
の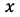 での微分は以下の通りになります。
での微分は以下の通りになります。
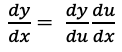
多変数関数の場合を考えてみる。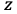 が
が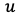 ,
,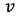 の関数で
の関数で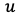 ,
,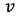 が
が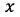 ,
,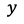 の関数であるとき
の関数であるとき
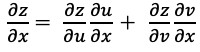
となります。
より一般的ににすると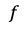 が
が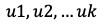 の関数で
の関数で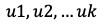 が
が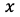 の関数のとき
の関数のとき
誤差逆伝播法
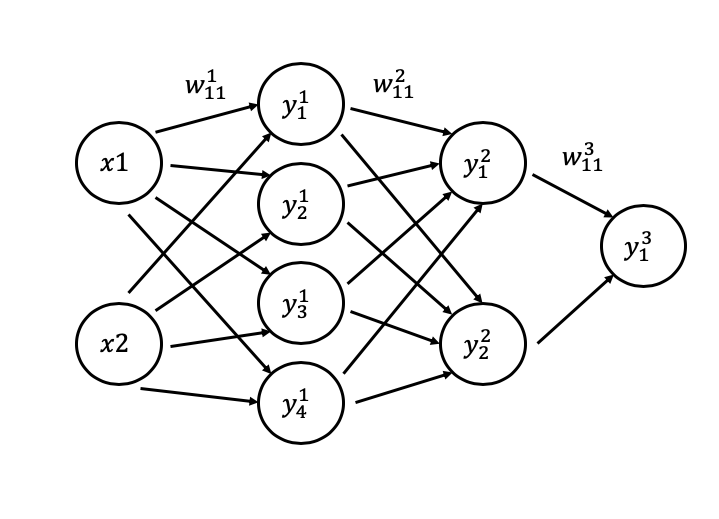
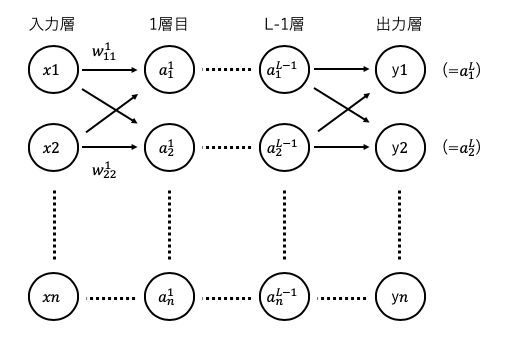
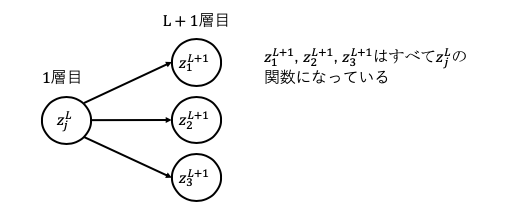
以下のようなニューラルネットワークで考えてみる。
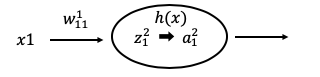
なお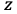 は重み付き和で
は重み付き和で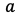 は活性化関数による変換後の値で
は活性化関数による変換後の値で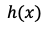 は活性化関数を示しています。
は活性化関数を示しています。
と表すことができます。
では本題に入りまして、誤差逆伝播法を適用していきましょう。
ここでは考えやすいように損失関数に2乗誤差を、出力層の活性化関数に恒等関数を用いた回帰問題について考えていきます。
今知りたいのは、損失関数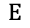 を重みパラメータ
を重みパラメータ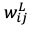 で偏微分した
で偏微分した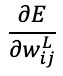 を求めることです。
を求めることです。
まず出力層の重みパラメータを考え、微分の連鎖律を使うと以下のようになります。
求める値が右辺に2項に分解したので1項ずつ求めます。
よって
となる。
続いて1項目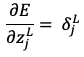 と置く。
と置く。
微分の連鎖律を使って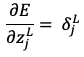 を変形していくと
を変形していくと
となり、出力層の活性化関数に恒等関数を用いているため、2項目は1となります。よって求めるべきは1項目であるから
よって
となります。
同様に中間層についても考えてみる。
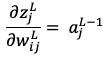 かつ
かつ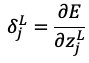 であるから
であるから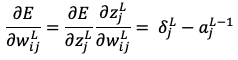 と置き換えることができ、以下のような式になります。
と置き換えることができ、以下のような式になります。
すべての項を合わせると
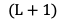 番目、つまり1つ先の
番目、つまり1つ先の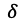 をずっと辿っていくと出力層の
をずっと辿っていくと出力層の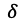 にたどり着く。
にたどり着く。
なお出力層の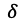 は以下の式のように簡単に求められました。
は以下の式のように簡単に求められました。
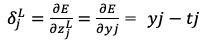
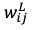 における勾配を求めるためには出力層から
における勾配を求めるためには出力層から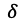 (誤差)を伝達してくれば良い。
(誤差)を伝達してくれば良い。
この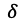 が出力層から伝わってくる様子から逆伝播と呼ばれています。
が出力層から伝わってくる様子から逆伝播と呼ばれています。
難しい数式だらけでしたが以上が誤差逆伝播法の解説でした。