近年話題のDeepLearning(深層学習)はニューラルネットワークを応用してできている。ニューラルネットワークを理解するには単純パーセプトロン、多層パーセプトロンの理解が必要となります。
今回は、このパーセプトロンについての概要をメモとして残しておきます。
単純パーセプトロン
視覚と脳の機能をモデル化したものであり、パターン認識を行う。シンプルなネットワークでありながら学習能力を持つ。1960年代に爆発的なニューラルネットブームを巻き起こしたが、1969年に人工知能学者マービン・ミンスキーらによって線形分離可能なものしか学習できないことが指摘されたことによって下火となった。他の研究者によってさまざまな変種が考案されており、ニューロン階層を多層化し入出力が二値から実数になったボルツマンマシン(1985年)やバックプロパゲーション(1986年)などによって再び注目を集めた。2009年現在でも広く使われている機械学習アルゴリズムの基礎となっている。 (Wikipedia)
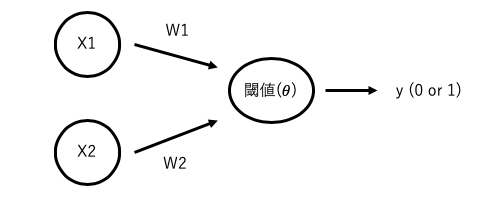
上記の図のように、入力x1、重みw1の積と入力x2、重みw2の積を足し合わせたものがある閾値を超えていなければ0、超えていれば1を出力するモデルとなっています。
数式にすると以下の通りです。
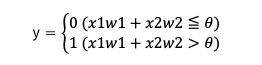
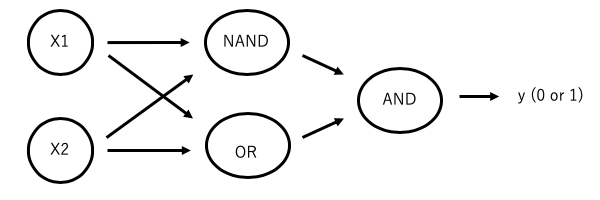
この単純パーセプトロンを論理回路を用いて考えてみましょう。
- AND(論理積)
AND回路の出力は以下の表のようになります。
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
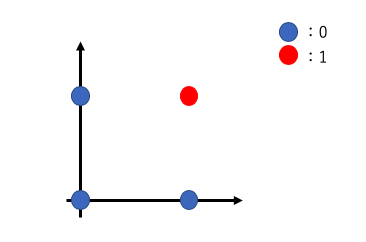
入力x1,x2が1の時のみ出力yが1を出力する回路です。
これを単純パーセプトロンの数式
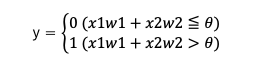
のパラメータwとθを求めると、w1=0.5、w2=0.5、θ=0.7などで式の条件を満たすことができます。よってAND回路は単純パーセプトロンで表現することが可能だということがわかります。
- OR(論理和)
OR回路の出力は以下の表のようになります。
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
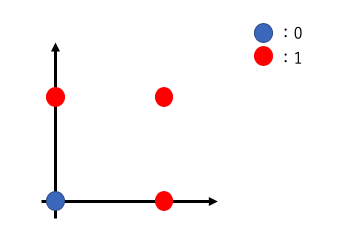
入力x1,x2のどちらか一方、または両方が1の時に出力yが1を出力する回路です。
パラメータwとθを求めると、w1=0.5、w2=0.5、θ=-0.2などで式の条件を満たすことができます。よってOR回路も単純パーセプトロンで表現することが可能だということがわかります。
- NAND(論理積の否定)
NAND回路の出力は以下の表のようになります。
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
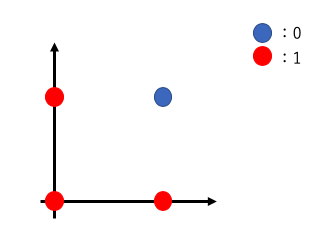
AND回路の逆バージョンになります。
パラメータwとθを求めると、w1=-0.5、w2=-0.5、θ=-0.7などで式の条件を満たすことができます。よってNAND回路も単純パーセプトロンで表現することが可能だということがわかります。
上記のようにAND、OR、NAND回路は問題なく表現することがわかりました。
- XOR(排他的論理和)
XOR回路の出力は以下の表のようになります。
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
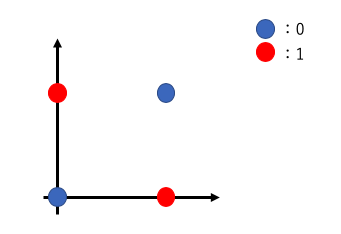
このXOR回路は、パラメータをどのように調整しても式の条件を満たすことはできません。
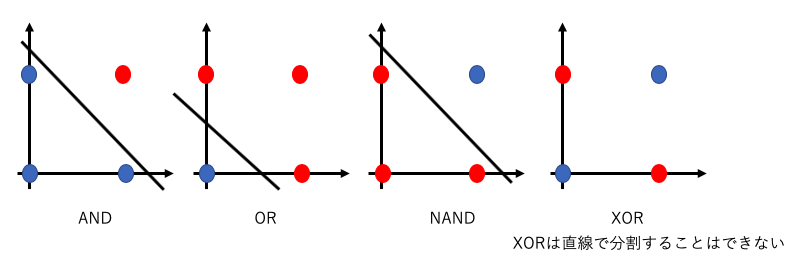
上記の図のように、単純パーセプトロンは直線で表現(線形分離可能な問題)することしかできず、XORのような非線形の領域を表現することはできません。
多層パーセプトロン
単純パーセプトロンでは表現できなかった、非線形の領域はパーセプトロンの層を重ねることで表現できます。
| x1 | x2 | NAND | OR | AND | y |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 |
3種類の論理ゲートを組み合わせることで、元の入力が排他的論理和の出力となることがわかりました。
ただし、今の形では出力yが0,1のみであるため現実の問題に適用できるとは思えません。
・回帰問題の出力は連続した実数値
・分類問題の出力は確率
上記のように出力を適切な形に変換する必要があります。
なお多層パーセプトロンは入力層と出力層しかなかった単純パーセプトロンに中間層(隠れ層)を追加したモデルで中間層と出力層の値を以下の活性化関数で変換する必要があります。
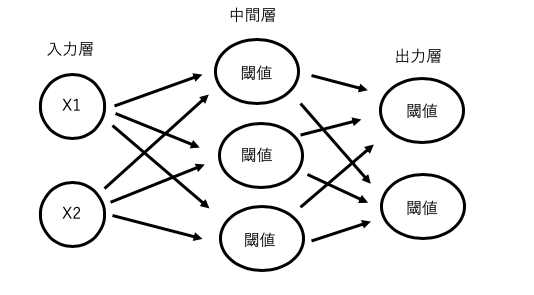
活性化関数
活性化関数(かっせいかかんすう、英: activation function)もしくは伝達関数(でんたつかんすう、英: transfer function)とは、ニューラルネットワークにおいて、線形変換をした後に適用する非線形関数もしくは恒等関数のことである。(Wikipedia)
説明の意味がいまいちわからないと思いますが、入力の重み付き和をある閾値を境に0,1に変換していました。このように重み付き和をある出力に変換する関数を活性化関数を呼びます。今回は活性化関数の種類と用途について説明します。
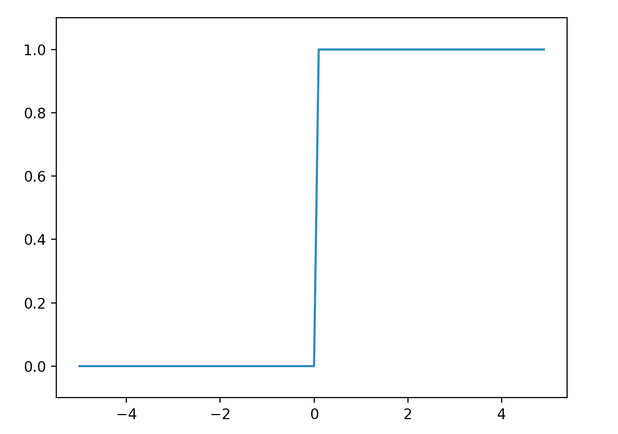
- ステップ関数
入力が0以上の時に1を出力し、入力が0以下の時に0を出力する関数。
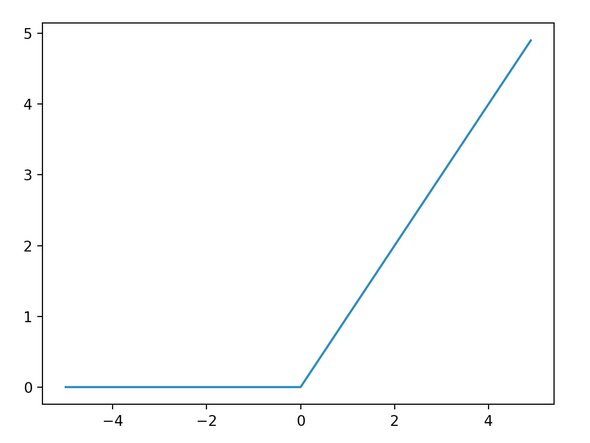
- ReLU関数
入力が0以上ならその値をそのまま出力し、0以下なら0を出力する関数(入力の重要度を出力に反映する)。
ほとんどの場合、中間層の活性化関数にはこのReLU関数が用いられる。
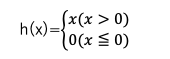
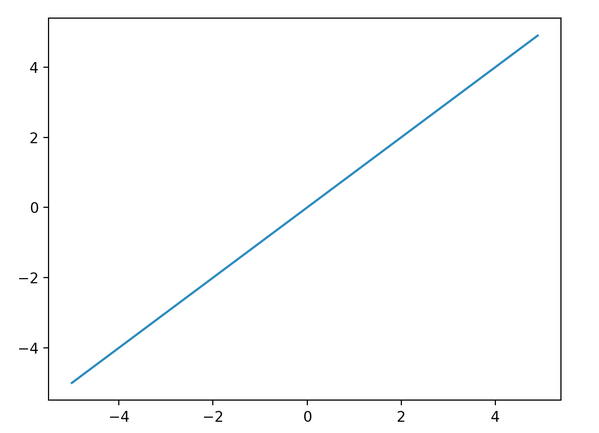
- 恒等関数
入力をそのまま出力とする関数。回帰問題における出力層の活性化関数に用いられる。
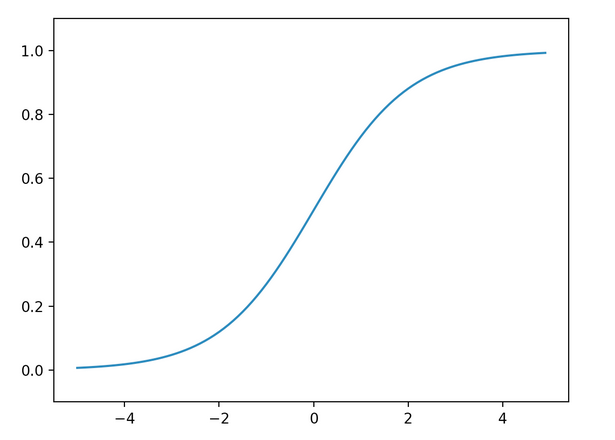
- シグモイド関数
0から1を出力する関数。確率を出力していると解釈できるため2値分類の出力層で用いられる。
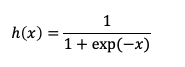
- ソフトマックス関数
多値分類問題に用いられる関数。多層パーセプトロンで多値分類を行う場合は、出力層のニューロンの数を分類するクラスの数と同じにする。
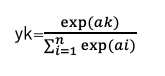
特徴はn個の出力の総和が1になる。つまりどのクラスに属しているのか予測することができる。
今回は、本当にざっくりではありますが、パーセプトロン出力の原理とその出力を適切な形に変換する活性化関数の説明をしました。
次回は、学習方法について理解していきたいと思います。