前回の記事では施設配置問題の概観と、その中で特に

容量制約なし施設配置問題
p-median 問題
p-center 問題

を取り上げました。今回の記事ではまだ取り上げていない問題の中から 被覆問題 を取り上げます。

集合被覆問題

集合被覆問題 (Set Covering Location Problem; SCLP) は、顧客全員をカバーできるような施設の配置のうち、もっとも施設数が少ない場合を求める問題です。

この問題は p-median 問題等と同様、 S.L.Hakimi 氏が1965年に初めてモデルをまとめ上げました。このモデルを整数計画問題としてまとめたのは C.Toregas 氏で、1971年になります。

式の形は以下

\text{Min} \quad \sum_{j \in V} x_j \\
\text{s.t.} \quad \sum_{j \in V_i} x_j \geq 1 \qquad \forall i \in V \\
\qquad x_j \in 0,1 \qquad \forall j \in V

それぞれの文字の意味は

$i$: 顧客のいる場所のインデックス
$j$: 施設の設置可能場所のインデックス
$V$: 顧客の集合
$V_i$: 顧客 $i$ から見て一定の距離以下の範囲にある $j$ の集合
$x_j$: 決定変数。$x_j = 1$ ならば場所 $j$ に施設を設置する。0ならば設置しない。

となります。

式の意味としては

目的関数: 施設の数を最小にする
制約条件: すべての顧客について、その周囲（近く）に少なくとも1つ施設がある

となります。

距離の許容範囲と V_i

被覆集合問題の場合、施設と顧客の間の距離は最大いくらまで許容されるのかが重要です。このパラメータは $s$ で表現されます。

先程の定式化の中で $V_i$ が登場しましたが、これは場所 $i$ から範囲 $s$ の中に含まれる、施設の設置可能場所 $j$ の集合ということになります。実際に Gurobi で計算を行う場合は、最適化計算を行う前にこの $V_i$ すべての $i$ について求めておく必要があるんじゃないかなって思います（もっと簡単な方法があれば教えてください）。

最大被覆問題

最大被覆問題は限られた施設数のなかでカバーする範囲を最大化せる場合を求める問題です。定式化は R.Church 氏と C.ReVelle 氏で、1974年になります（論文がフリーで公開されていました）。

式の形は以下

\text{Max} \quad \sum_{i \in V} a_i y_i \\
\text{s.t.} \quad \sum_{j \in V_i} x_j \geq y_i \qquad \forall i \in V \\
\qquad \sum_{j \in V} x_j = p \\
\qquad x_j \in 0, 1 \qquad \forall j \in V \\
\qquad y_i \in 0, 1 \qquad \forall i \in V

それぞれの文字の意味は

$i$: 顧客のいる場所のインデックス
$j$: 施設の設置可能場所のインデックス
$V$: 顧客の集合
$V_i$: 顧客 $i$ から見て一定の距離以下の範囲にある $j$ の集合
$a_i$: 場所 $i$ における顧客の需要の量
$p$: 施設の設置数
$x_j$: 決定変数。$x_j = 1$ ならば場所 $j$ に施設を設置する。0ならば設置しない。
$y_i$: 決定変数。$y_i = 1$ ならば顧客 $i$ はどこかしらの施設にカバーされている。0ならばカバーされていない。

となります。

式の意味としては

目的関数: カバーされる顧客の需要の総数を最大化する
制約条件1: 顧客 $i$ の周辺（近く）に施設が設置されない限り、顧客 $i$ はカバーされたとは言えない
制約条件2: 設置する施設の数は $p$ 個

となります。

Gurobi による実装

集合被覆問題

問題設定を以下のようにしてみます。

client = {
    0: {"name": "Client 0", "covered by": [0, 1, 4]},
    1: {"name": "Client 1", "covered by": [0]},
    2: {"name": "Client 2", "covered by": [2, 3, 4]},
    3: {"name": "Client 3", "covered by": [2, 5]},
    4: {"name": "Client 4", "covered by": [2, 5]},
    5: {"name": "Client 5", "covered by": [0, 3]},
    6: {"name": "Client 6", "covered by": [2, 3, 4]},
    7: {"name": "Client 7", "covered by": [1, 4]},
    8: {"name": "Client 8", "covered by": [1, 4, 5]},
}

facility = {
    0: {"name": "Facility 0", "cover": [0, 1, 5]},
    1: {"name": "Facility 1", "cover": [0, 7, 8]},
    2: {"name": "Facility 2", "cover": [2, 3, 4, 6]},
    3: {"name": "Facility 3", "cover": [2, 5, 6]},
    4: {"name": "Facility 4", "cover": [0, 2, 6, 7, 8]},
    5: {"name": "Facility 5", "cover": [3, 4, 8]},
}

"cover" と "covered by" はそれぞれ

施設を建てる候補地はそれぞれどの顧客をカバーできるか
それぞれの顧客はどの施設候補地にカバーされることができるか

を表しています。

これに対して集合被覆問題の計算を行ってみます。

from gurobipy import *

# モデルの構築
m = Model()

# 決定変数
x = {}
for j in range(len(facility)):
    x[j] = m.addVar(vtype=GRB.BINARY, name="x%d" % j)

m.update()

# 制約条件
for i in range(len(client)):
    m.addConstr( quicksum(x[j] for j in client[i]["covered by"]) >= 1 )

# 目的関数
m.setObjective( quicksum( x[j] for j in range(len(facility)) ), GRB.MINIMIZE )

# 計算の実行
m.optimize()

これで計算ができました。結果を NetworkX で可視化してみます。

import matplotlib.pyplot as plt
import networkx as nx

fig = plt.figure(figsize=(6, 6))
ax = plt.subplot(111)
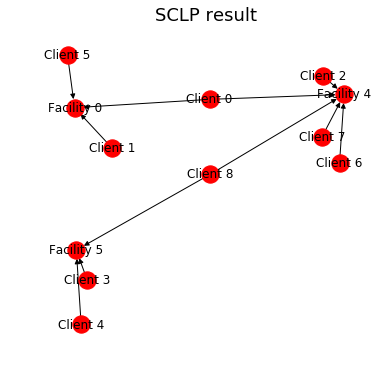
ax.set_title("SCLP result", fontsize=18)

G = nx.DiGraph()

for key_client in client:
    G.add_node(client[key_client]["name"])

for key_facility in facility:
    if x[key_facility].x == 1:
        G.add_node(facility[key_facility]["name"])

# 計算結果となるエッジを追加
for key_facility in facility:
    if x[key_facility].x == 1:
        for i in facility[key_facility]["cover"]:
            G.add_edge(client[i]["name"], facility[key_facility]["name"])

nx.draw(G, with_labels=True)
plt.savefig("sclp_result.png", format="PNG")
plt.show()

結果が得られました。設置された施設は "Facility 0", "Facility 4", "Facility 5" の3つであることがわかります。

最大被覆問題

問題設定を以下のようにしてみます。基本的には先程の集合被覆問題と同じです。

先程の集合被覆問題の計算で、全体をカバーするのに最低3つの施設が必要だということがわかったので、ここでは施設の数を 2 つに限定してみます。

client = {
    0: {"name": "Client 0", "covered by": [0, 1, 4]},
    1: {"name": "Client 1", "covered by": [0]},
    2: {"name": "Client 2", "covered by": [2, 3, 4]},
    3: {"name": "Client 3", "covered by": [2, 5]},
    4: {"name": "Client 4", "covered by": [2, 5]},
    5: {"name": "Client 5", "covered by": [0, 3]},
    6: {"name": "Client 6", "covered by": [2, 3, 4]},
    7: {"name": "Client 7", "covered by": [1, 4]},
    8: {"name": "Client 8", "covered by": [1, 4, 5]},
}

facility = {
    0: {"name": "Facility 0", "cover": [0, 1, 5]},
    1: {"name": "Facility 1", "cover": [0, 7, 8]},
    2: {"name": "Facility 2", "cover": [2, 3, 4, 6]},
    3: {"name": "Facility 3", "cover": [2, 5, 6]},
    4: {"name": "Facility 4", "cover": [0, 2, 6, 7, 8]},
    5: {"name": "Facility 5", "cover": [3, 4, 8]},
}

p = 2

計算を行います。

from gurobipy import *

# モデルの構築
m = Model()

# 決定変数
x = {}
y = {}

for j in range(len(facility)):
    x[j] = m.addVar(vtype=GRB.BINARY, name="x%d" % j)

for i in range(len(client)):
    y[i] = m.addVar(vtype=GRB.BINARY, name="y%d" % i)

m.update()

# 制約条件
for i in range(len(client)):
    m.addConstr( quicksum(x[j] for j in client[i]["covered by"]) >= y[i] )

m.addConstr( quicksum(x[j] for j in range(len(facility)) ) == p )

# 目的関数
m.setObjective( quicksum(client[i]["population"] * y[i] for i in range(len(client))) , GRB.MAXIMIZE)

# 計算の実行
m.optimize()

これで計算結果が得られました。可視化してみます。

import matplotlib.pyplot as plt
import networkx as nx

fig = plt.figure(figsize=(6, 6))
ax = plt.subplot(111)
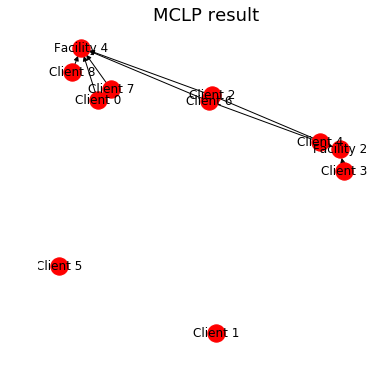
ax.set_title("MCLP result", fontsize=18)

G = nx.DiGraph()

for key_client in client:
    G.add_node(client[key_client]["name"])

for key_facility in facility:
    if x[key_facility].x == 1:
        G.add_node(facility[key_facility]["name"])

for key_facility in facility:
    if x[key_facility].x == 1:
        for i in facility[key_facility]["cover"]:
            if y[i].x == 1:
                G.add_edge(client[i]["name"], facility[key_facility]["name"])

nx.draw(G, with_labels=True)
plt.savefig("mclp_result.png", format="PNG")
plt.show()

施設が2つだと確かにカバーできない顧客が発生してしまうことが確認されました。

参考文献

『Foundation of Location Analysis』 H.A.Eiselt, Vladimir Marianov

Cell Tower Coverage with integer programming and Gurobi

施設配置問題としての被覆問題と Gurobi による実装

集合被覆問題

距離の許容範囲と V_i

最大被覆問題

Gurobi による実装

集合被覆問題

最大被覆問題

参考文献