施設配置問題 (Facility Location Problem) と Gurobi による実装

施設配置問題の種類

施設配置問題 (Facility Location Problem) とは、日本オペレーションズ・リサーチ学会の Wiki に基づくと

施設の配置可能地点, 需要をもつ顧客の集合が与えられて, ある基準を満たす施設の配置場所を決定する問題の総称

と定義されます。

例えばイギリスの各地に分布しているスーパーマーケット（需要を持つ顧客）に対して、商品の倉庫（施設）をどう設置すれば輸送コストと建設コストの和を最も抑えることができるか、といったことを考えます（下図）。

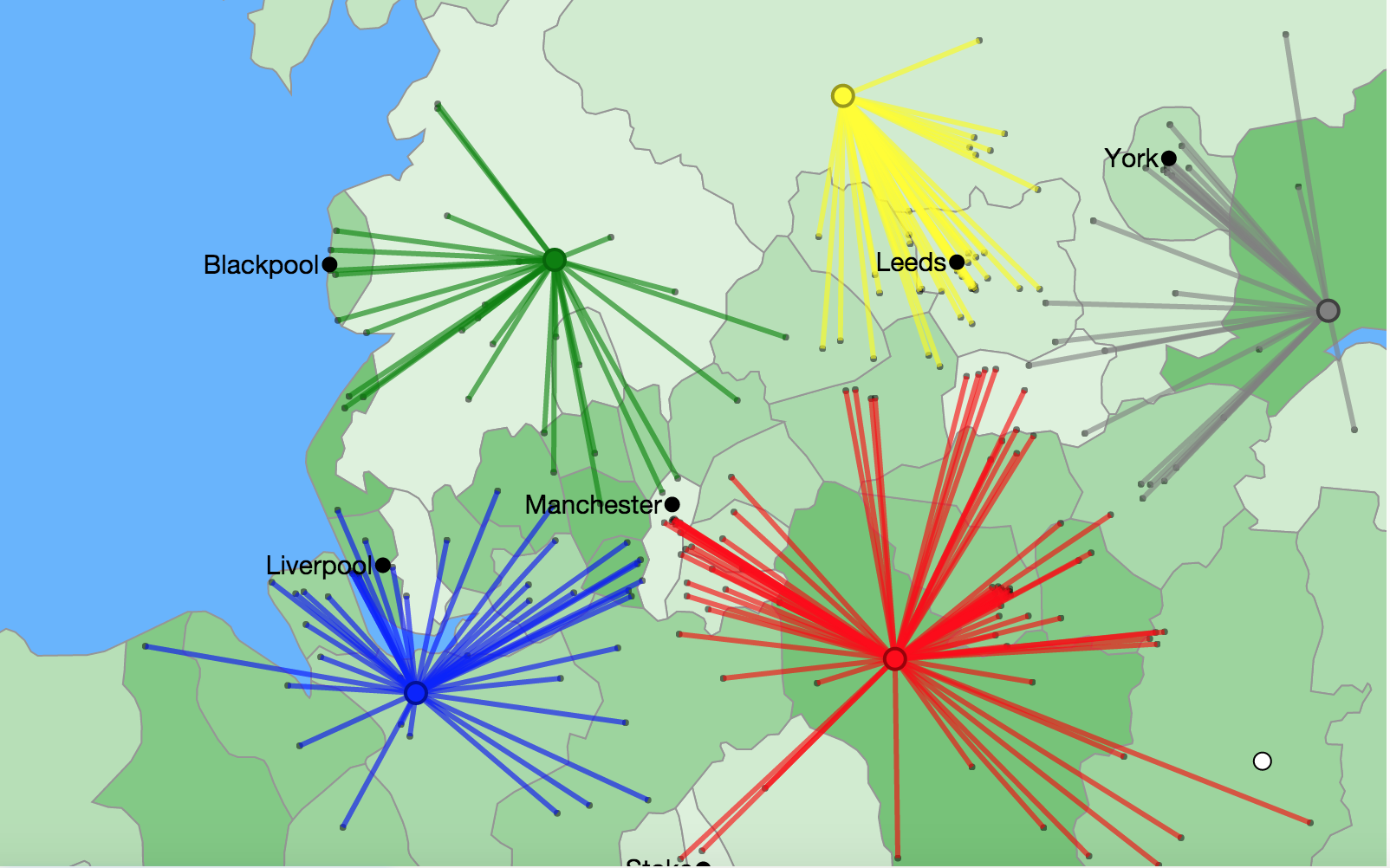（図は http://examples.gurobi.com/facility-location/ より）

ただし、一口に施設配置問題と言っても複数のバリエーションがあり、それぞれ目的関数の立て方などが異なります。

最小コストで顧客全員にサービス提供できる施設の数と配置を考える

目的関数は、施設の設置コストと輸送コストの和の最小化。先程の図の例が該当します。

• 施設1つあたりのサービス提供能力に制限が無い場合
  • 容量制約なし施設配置問題 (Uncapacitated Facility Location Problem; UFLP)
• 施設1つあたりのサービス提供能力に制限がある場合
  • 容量制約付き施設配置問題 (Capacitated Facility Location Problem; CFLP)

施設の数は p 個で固定にし、顧客全員にサービス提供できる配置を考える

目的関数は以下の2つのとり方があります。

• 顧客・施設間の距離の総和を最小化する（Minisum）
  • p-median 問題
• 顧客・施設間の距離の最大値を最小化する（Minimax）
  • p-center 問題

顧客のカバー率を考える（被覆問題）

• 最小コストで全員をカバーできる配置を求める
  • 集合被覆問題 (Set Covering Location Problem; SCLP)
• 特定の予算でカーバできる領域を最大化させる
  • 最大被覆問題 (Maximal Covering Location Problem; MCLP)

他社がすでに進出しているエリアに対して自社の施設を配置してシェアを奪う場合を考える

• 競合施設配置問題 (Competitive Location Models)

単純に施設配置問題と言っても上記のように様々なバリエーションがあるので、自分が解きたい問題が施設配置問題の中のどれに該当するのかを正しく判断することが大切かと思います。

UFLP と p-median の違い

UFLP と p-median は先程の説明でも感じられたかと思いますがとても似ています。実際、 p-median 問題の p の値を変動させる場合を考えれば UFLP に近い分析が可能です。この2つの違いは

1. UFLPでは場所ごとに設置コストがいくらになるのか考えるが、p-median ではどの場所に設置してもコストは変わらないという前提がある
2. UFLPでは施設の建設数に制限が無いが、p-medinaは p 個という制限がある
3. UFLPは大抵の場合だと顧客と施設の場所が別々に用意されることになるが、p-medianでは顧客のいる場所に施設を設置するということも可能

というのが挙げられています（ https://pdfs.semanticscholar.org/111a/92b71a4adb8ace1cb1ac4b2f2ab5f5811c99.pdf ）。

以下では施設配置問題のうち、有名な UFLP, p-median, p-center を概観したあと、gurobi で実際に計算をしてみようと思います。

UFLP

UFLPは施設の設置コストとサービスの輸送コストを吟味して、総コストが最小になるような施設の数とその設置場所を求めます。式は以下のように記述されます。

\text{Max} \quad \sum_i \sum_j c_{ij} x_{ij} + \sum_i f_i y_i \\
\text{s.t.} \quad \sum_i x_{ij} = 1 \quad \forall j \\
\qquad x_{ij} \leq y_i \quad \forall i,j \\
\qquad x_{ij} \geq 0 \quad \forall i,j \\
\qquad y_i \in {0, 1} \quad \forall i,j

それぞれの文字の意味は

• $c_{ij}$: 地点$i$ の施設が地点$j$ の顧客へサービス提供する際の総コスト
• $f_i$: 地点 $i$ に施設を設置する際のコスト
• $x_{ij}$: 決定変数。地点$j$ の顧客の需要量全体を1としたときの、地点 $i$ の施設が解決した地点$j$ の顧客の需要量が占める割合
• $y_i$: 決定変数。$y_i = 1$ ならば地点$i$ に施設を設置する。0ならば設置しない。

式の意味としては

目的関数 : （顧客へのサービス提供にかかるコスト） + （施設の固定費） を最小化させる
制約条件1 : 地点$j$ にいる顧客の需要は、合計すると1になる
制約条件2 : 地点 $i$ に施設が建設されない場合 ($y_i = 0$)、地点 $i$ でのサービス提供はない
制約条件3 : $x_ij$ （地点 $j$ の顧客の需要のうち地点 $i$ において解決される量） は0以上
制約条件4 : $y_i$ （地点 $i$ に施設を建設するか否か） は 0 か 1 の値しか取らない

となります。

アルゴリズム

UFLPを解くアルゴリズムは Efroymson 氏と Ray 氏が1966年に発表した分枝限定法 (Branch-and-Bound; BB) を用いる方法や、Donald Erlenkotter 氏が1978年に発表した双対上昇法 (Dual Ascent Method) による方法などが挙げられます。どうやら双対上昇法のほうがより効率的であるようですが、 Gurobi などのソルバーを使う場合はそもそもソルバーに実装されている混合整数計画問題のアルゴリズムを使うことになると思うので分枝限定法ベースの解き方になるのかなと思います。

p-median 問題

p-median 問題は、施設の数が p 個で固定の状態で、顧客と施設の間の距離の合計が最小となるような施設の配置を考えます。距離の合計が最小になるということは、輸送コストが最小になると捉えてもよいかと思います。現実的な話として、建設する施設の数が p 個と決まっている場合とはどんなときなのだろうかと私は少し疑問に思いました。調べてみたところ、政治的な理由で施設数が決まっている場合や、全体の予算が決まっていてかつどこに施設を設置してもコストが対して変わらない場合などが該当するようです。

p-median 問題の前提条件

p-median 問題は以下のような前提をまず置きます。

• 設置する施設は p 個で固定
• 施設と顧客の対応関係が特に指定されない場合、顧客は自身の最寄りの施設を利用する
• 顧客は最寄りの施設に向けて最短経路をたどって移動する

二番目の前提は結果的に、__同じエリアの顧客は同じ最寄りの施設を利用する__ことに繋がります。そのためもしも得られた計算結果に、同じエリアの顧客なのに異なる施設を利用していることがあったら、それは最適解ではない可能性が高いと言えます。というのも、2つの施設が等距離に無い限り、より近い側の施設を利用すればコストの削減が可能になるからである（もちろん施設のサービス提供能力に制限があればこの限りではないです。いわゆる Allocation の問題になりますが、ここでは割愛します）。

p-median問題の定式化

p-median 問題は S.L.Hakimi 氏が1964年に提出した論文が始まりとされています。この論文はグラフ理論で "absolute median" （良い日本語訳がよくわかりません）を求める手法を取り扱っています。 実はこのタイミングでは整数計画問題の形の記述がされていませんでした。 p-median 問題を整数計画問題として初めて定式化を行ったのは Charles S. ReVelle 氏と Ralph Swain 氏で、1970年になります（ちなみにこのふたりは Hakimi 氏の論文との関連性に言及はしておらず、 median という表現もしていませんでした）。

ReVelle氏とSwain氏による定式化は今日使われているもので、以下の形になります。

\text{Min} \quad \sum_{i,j} h_i d_{ij} x_{ij}\\
\text{s.t.} \quad \sum_j x_{ij} = 1 \qquad \forall i \\
\qquad x_{ij} \leq y_{j} \qquad \forall i, j \\
\qquad \sum_j y_j = p \\
\qquad x_{ij}, y_j \in 0,1 \qquad \forall i, j

それぞれの文字の意味は

• $i$: 顧客いる場所のインデックス
• $j$: 施設の設置可能場所のインデックス
• $m$: 施設の設置可能場所の総数
• $n$: 顧客のいる場所の総数
• $p$: 施設を設置実際に設置する場所の総数
• $h_i$: 顧客のいるそれぞれの場所における需要の量
• $d_{ij}$: 顧客のいる場所 $i$ と施設の設置可能場所 $j$ との間の距離
• $x_{ij}$: 決定変数。$x_{ij} = 1$ ならば場所$i$ にいる顧客は場所 $j$ の施設を利用する。0ならばそうではない。
• $y_j$: 決定変数。$y_{j} = 1$ ならば場所 $j$ に施設を設置する。0ならばそうではない。

です。p-median問題の前提から特定の場所の顧客はすべて同じ最寄りの施設を使うという条件が定まることから、決定変数 $x_{ij}$ はそれに基づいた形をしていることがわかります。

アルゴリズム

p-median 問題を解く方法には複数の方法としては

• 厳密解を求める方法（分枝限定法）
• ヒューリスティックな方法

が挙げられます。UFLPと同様に Gurobi に実装されている混合整数計画問題のアルゴリズムは分枝限定法ベースのものになります。

p-center 問題

先程 p-median 問題が S.L.Hakimi 氏の論文から始まったと述べましたが、同じ論文のなかで "absolute center" という概念も登場してきています。この absolute center が今の p-center 問題の元祖に当たるとされています。

p-center 問題は救急車の配置や消防施設の配置など、エリア全体をカバーする際の移動距離が一定値以下になるような施設の配置を求める問題になります。 p-center 問題の混合整数計画問題による立式は以下のようになります。

\text{Min} \quad W \\
\text{s.t.} \quad \sum_{j} x_{ij} = 1 \qquad \forall i \\
\qquad \sum_{j} y_j = p \\
\qquad x_{ij} \leq y_j \qquad \forall i,j \\
\qquad W \geq \sum_{j} h_i d_{ij} x_{ij} \qquad \forall i \\
\qquad y_j \in 0, 1 \qquad \forall j \\
\qquad x_{ij} \geq 0 \qquad \forall i,j

それぞれの文字の意味は

• $i$: 顧客いる場所のインデックス
• $j$: 施設の設置可能場所のインデックス
• $m$: 施設の設置可能場所の総数
• $n$: 顧客のいる場所の総数
• $p$: 施設を設置実際に設置する場所の総数
• $h_i$: 顧客のいるそれぞれの場所における需要の量
• $d_{ij}$: 顧客のいる場所 $i$ と施設の設置可能場所 $j$ との間の距離
• $x_{ij}$: 決定変数。$x_{ij} = 1$ ならば場所$i$ にいる顧客は場所 $j$ の施設を利用する。0ならばそうではない。
• $y_j$: 決定変数。$y_{j} = 1$ ならば場所 $j$ に施設を設置する。0ならばそうではない。
• $W$: 決定変数。顧客から施設までの移動コストの上限値

Gurobi による実装

UFLP

まず問題設定を以下のようにします。

client = {
    0: {"name": "Client 0", "pos": (0, 1.5), "demand": 1},
    1: {"name": "Client 1", "pos": (2.5, 1.2), "demand": 1}
}

facility = {
    0: {"name": "Facility 0", "pos" : (0, 0), "charge" : 3},
    1: {"name": "Facility 1", "pos" : (0, 1), "charge" : 2},
    2: {"name": "Facility 2", "pos" : (0, 2), "charge" : 3},
    3: {"name": "Facility 3", "pos" : (1, 0), "charge" : 2},
    4: {"name": "Facility 4", "pos" : (1, 1), "charge" : 3},
    5: {"name": "Facility 5", "pos" : (1, 2), "charge" : 3},
    6: {"name": "Faciliyt 6", "pos" : (2, 0), "charge" : 4},
    7: {"name": "Facility 7", "pos" : (2, 1), "charge" : 3},
    8: {"name": "Facility 8", "pos" : (2, 2), "charge" : 2},
}

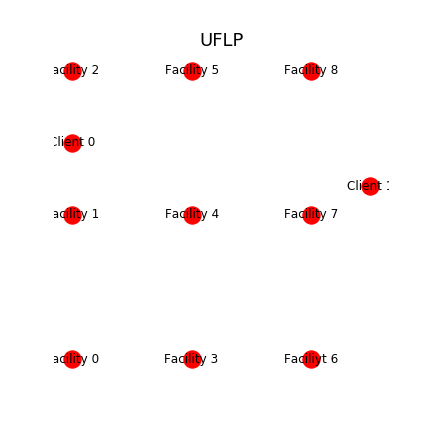
NetworkX で可視化してみると以下の通り

import matplotlib.pyplot as plt
import networkx as nx

fig = plt.figure(figsize=(6, 6))
ax = plt.subplot(111)
ax.set_title("UFLP", fontsize=18)

G = nx.DiGraph()

for key_client in client:
    G.add_node(client[key_client]["name"])

for key_facility in facility:
    G.add_node(facility[key_facility]["name"])
    
pos = {}
for key_client in client:
    pos[client[key_client]["name"]] = client[key_client]["pos"]

for key_facility in facility:
    pos[facility[key_facility]["name"]] = facility[key_facility]["pos"]
    
nx.draw(G, pos, with_labels=True)
plt.savefig("UFLP.png", format="PNG")
plt.show()

この条件下で UFLP を行ってみます。

from gurobipy import *
import math

# 距離
def distance(a,b):
    dx = a[0] - b[0]
    dy = a[1] - b[1]
    return math.sqrt(dx*dx + dy*dy)

d = {}
for i in range(len(client)):
    for j in range(len(facility)):
        d[(i,j)] = distance(client[i]["pos"], facility[j]["pos"])

# モデルの構築
m = Model()

# 決定変数
x = {}
y = {}

for i in range(len(client)):
    for j in range(len(facility)):
        x[(i,j)] = m.addVar(lb=0, vtype=GRB.CONTINUOUS, name="x%d,%d" % (i,j))

for j in range(len(facility)):
    y[j] = m.addVar(vtype=GRB.BINARY, name="y%d" % j)

m.update()

# 制約条件
for i in range(len(client)):
    for j in range(len(facility)):
        m.addConstr(x[(i,j)] <= y[j])

for i in range(len(client)):
    m.addConstr(quicksum(x[(i,j)] for j in range(len(facility))) == 1)

# 目的関数
m.setObjective( quicksum(facility[j]["charge"]*y[j] + quicksum(client[i]["demand"]*d[(i,j)]*x[(i,j)]
                for i in range(len(client))) for j in range(len(facility))) )

# 計算の実行
m.optimize()

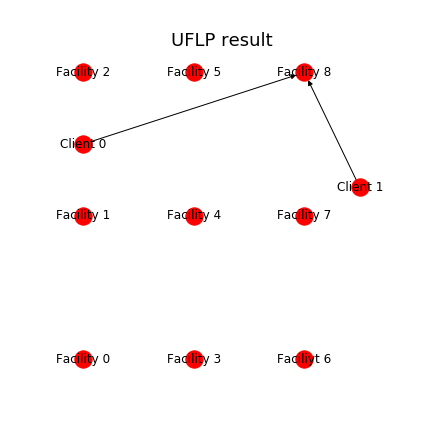
これで計算結果が得られたので、可視化してみます。

fig = plt.figure(figsize=(6, 6))
ax = plt.subplot(111)
ax.set_title("UFLP result", fontsize=18)

G = nx.DiGraph()

for key_client in client:
    G.add_node(client[key_client]["name"])

for key_facility in facility:
    G.add_node(facility[key_facility]["name"])
    
pos = {}
for key_client in client:
    pos[client[key_client]["name"]] = client[key_client]["pos"]

for key_facility in facility:
    pos[facility[key_facility]["name"]] = facility[key_facility]["pos"]
    
# 計算結果のエッジを追加
for i in range(len(client)):
    for j in range(len(facility)):
        if x[(i, j)].x == 1:
            G.add_edge(client[i]["name"], facility[j]["name"])
    
nx.draw(G, pos, with_labels=True)
plt.savefig("UFLP_result.png", format="PNG")
plt.show()

答えが得られました。

p-median

問題設定を以下のようにします。

client = {
    0: {"name": "Client 0", "pos": (0, 1.5), "demand": 1},
    1: {"name": "Client 1", "pos": (2.5, 1.2), "demand": 1}
}

facility = {
    0: {"name": "Facility 0", "pos" : (0, 0), "charge" : 3},
    1: {"name": "Facility 1", "pos" : (0, 1), "charge" : 2},
    2: {"name": "Facility 2", "pos" : (0, 2), "charge" : 3},
    3: {"name": "Facility 3", "pos" : (1, 0), "charge" : 2},
    4: {"name": "Facility 4", "pos" : (1, 1), "charge" : 3},
    5: {"name": "Facility 5", "pos" : (1, 2), "charge" : 3},
    6: {"name": "Faciliyt 6", "pos" : (2, 0), "charge" : 4},
    7: {"name": "Facility 7", "pos" : (2, 1), "charge" : 3},
    8: {"name": "Facility 8", "pos" : (2, 2), "charge" : 2},
}

p = 2

先程とほとんど同じですが、施設の数を2つにしてみます。この条件下で p-median を行ってみます。

from gurobipy import *
import math

# 距離
def distance(a,b):
    dx = a[0] - b[0]
    dy = a[1] - b[1]
    return math.sqrt(dx*dx + dy*dy)

d = {}
for i in range(len(client)):
    for j in range(len(facility)):
        d[(i,j)] = distance(client[i]["pos"], facility[j]["pos"])

# モデルの構築
m = Model()

# 決定変数
x = {}
y = {}

for i in range(len(client)):
    for j in range(len(facility)):
        x[(i,j)] = m.addVar(lb=0, vtype=GRB.CONTINUOUS, name="x%d,%d" % (i,j))

for j in range(len(facility)):
    y[j] = m.addVar(vtype=GRB.BINARY, name="y%d" % j)

m.update()

# 制約条件
for i in range(len(client)):
    for j in range(len(facility)):
        m.addConstr(x[(i,j)] <= y[j])

for i in range(len(client)):
    m.addConstr(quicksum(x[(i,j)] for j in range(len(facility))) == 1)
    
m.addConstr(quicksum(y[j] for j in range(len(facility))) == p)
    
# 目的関数
m.setObjective( 
    quicksum( quicksum(client[i]["demand"] * d[(i, j)] * x[(i, j)] 
                       for i in range(len(client)) ) for j in range(len(facility)) )
)

# 計算の実行
m.optimize()

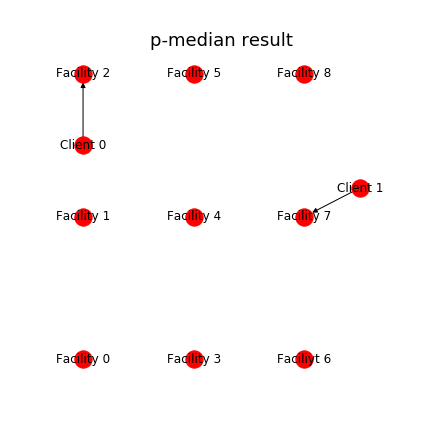
答えの可視化

fig = plt.figure(figsize=(6, 6))
ax = plt.subplot(111)
ax.set_title("p-median result", fontsize=18)

G = nx.DiGraph()

for key_client in client:
    G.add_node(client[key_client]["name"])

for key_facility in facility:
    G.add_node(facility[key_facility]["name"])

pos = {}
for key_client in client:
    pos[client[key_client]["name"]] = client[key_client]["pos"]

for key_facility in facility:
    pos[facility[key_facility]["name"]] = facility[key_facility]["pos"]

# 計算結果のエッジを追加
for i in range(len(client)):
    for j in range(len(facility)):
        if x[(i, j)].x == 1:
            G.add_edge(client[i]["name"], facility[j]["name"])

nx.draw(G, pos, with_labels=True)
plt.savefig("p-median_result.png", format="PNG")
plt.show()

移動距離が短くなるように計算するため、当然ながらそれぞれの client から最も近いところに施設が立てられていることがわかります。

p-center

p-median と同じ問題設定でやってみます。

from gurobipy import *
import math

# 距離
def distance(a,b):
    dx = a[0] - b[0]
    dy = a[1] - b[1]
    return math.sqrt(dx*dx + dy*dy)

d = {}
for i in range(len(client)):
    for j in range(len(facility)):
        d[(i,j)] = distance(client[i]["pos"], facility[j]["pos"])

# モデルの構築
m = Model()

# 決定変数
W = m.addVar(lb=0, vtype=GRB.CONTINUOUS, name="W")

x = {}
y = {}

for i in range(len(client)):
    for j in range(len(facility)):
        x[(i,j)] = m.addVar(lb=0, vtype=GRB.CONTINUOUS, name="x%d,%d" % (i,j))

for j in range(len(facility)):
    y[j] = m.addVar(vtype=GRB.BINARY, name="y%d" % j)

m.update()

# 制約条件
for i in range(len(client)):
    for j in range(len(facility)):
        m.addConstr(x[(i,j)] <= y[j])

for i in range(len(client)):
    m.addConstr(quicksum(x[(i,j)] for j in range(len(facility))) == 1)
    
m.addConstr(quicksum(y[j] for j in range(len(facility))) == p)

for i in range(len(client)):
    m.addConstr(W >= quicksum(client[i]["demand"] * d[(i, j)] * x[(i, j)] for j in range(len(facility)) ))
    
# 目的関数
m.setObjective(W)

# 計算の実行
m.optimize()

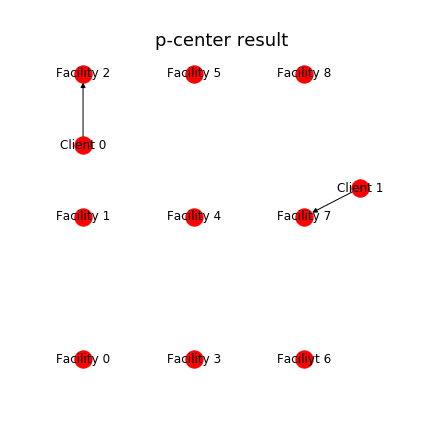
結果の可視化

fig = plt.figure(figsize=(6, 6))
ax = plt.subplot(111)
ax.set_title("p-center result", fontsize=18)

G = nx.DiGraph()

for key_client in client:
    G.add_node(client[key_client]["name"])

for key_facility in facility:
    G.add_node(facility[key_facility]["name"])
    
pos = {}
for key_client in client:
    pos[client[key_client]["name"]] = client[key_client]["pos"]

for key_facility in facility:
    pos[facility[key_facility]["name"]] = facility[key_facility]["pos"]
    
# 計算結果のエッジを追加
for i in range(len(client)):
    for j in range(len(facility)):
        if x[(i, j)].x == 1:
            G.add_edge(client[i]["name"], facility[j]["name"])
    
nx.draw(G, pos, with_labels=True)
plt.savefig("p-center_result.png", format="PNG")
plt.show()

問題設定がちょっとおもしろくなかったかもしれません。p-median と同じ結果ということになりましたが、まぁそうなるよなという感じです。

参考文献

『Foundation of Location Analysis』 H.A.Eiselt, Vladimir Marianov

日本オペレーションズ・リサーチ学会 Wiki

Facility Location with Integer Programming and Gurobi

Gurobi の使い方