夏のベンチマーク第二弾です (第一弾は こちら).
整数型の演算速度の比較をどこかで見た記憶があるのですが見つけられないので自前で試してみます.
問題とコード
四則計算に対応して 4 つの問題を 12 の整数型で試してみます. なおベンチマークは release ビルドなので, i8 や u8 のオーバーフローは wrapping として扱われます (参考文献).
- 和: Fibonacci 数列を計算
- 差: Euclid の互除法 (引き算で実装)
- 積: 階乗の計算
- 剰余: 完全数のリストアップ
# ![feature(test)]
extern crate test;
mod add {
macro_rules! fibonacci {
( $( $t: ident ), * ) => { $(
#[bench]
fn $t (b: &mut test::Bencher) {
b.iter(|| {
let mut state: [$t;2] = [ 0, 1 ];
for _ in 1..64 {
let x = test::black_box(state[0]) + test::black_box(state[1]);
state = [ state[1], x ];
}
});
}
) * }
}
fibonacci!(i8, i16, i32, i64, i128, isize, u8, u16, u32, u64, u128, usize);
}
mod sub {
macro_rules! euclid {
( $( $t: ident ), * ) => { $(
#[bench]
fn $t (b: &mut test::Bencher) {
let euclid = |mut m: $t, mut n: $t| {
while m > 0 {
while n >= m {
n -= test::black_box(m);
}
let swap = m;
m = n;
n = swap;
}
n
};
b.iter(|| {
assert_eq!( euclid(126, 27), 9 );
assert_eq!( euclid(120, 10), 10 );
assert_eq!( euclid(121, 33), 11 );
assert_eq!( euclid(108, 12), 12 );
});
}
) * }
}
euclid!(i8, i16, i32, i64, i128, isize, u8, u16, u32, u64, u128, usize);
}
mod mul {
macro_rules! factorial {
( $( $t: ident ), * ) => { $(
#[bench]
fn $t (b: &mut test::Bencher) {
b.iter(|| {
for n in (1 as $t)..96 {
let n = test::black_box(n);
let _ = (1..n+1).fold(1, |r,i| r*i);
}
});
}
) * }
}
factorial!(i8, i16, i32, i64, i128, isize, u8, u16, u32, u64, u128, usize);
}
mod rem {
macro_rules! perfect {
( $( $t: ident ), * ) => { $(
#[bench]
fn $t (b: &mut test::Bencher) {
b.iter(|| {
assert_eq!(
(1..33).filter(|&n| {
let n: $t = test::black_box(n);
(1..n).filter(|&i| n%i==0).sum::<$t>() == n
}).count(),
2
);
});
}
) * }
}
perfect!(i8, i16, i32, i64, i128, isize, u8, u16, u32, u64, u128, usize);
}
結果
環境は Debian 10.0 on Win10 1903 64bit (WSL), Intel Core i7-6700 @3.40GHz, rustc 1.38.0-nightly (534b42394 2019-08-09) です.
$ cargo +nightly bench
Finished release [optimized] target(s) in 0.01s
Running target/release/deps/integer-a6438b606d266f3c
running 48 tests
test add::i128 ... bench: 89 ns/iter (+/- 7)
test add::i16 ... bench: 88 ns/iter (+/- 10)
test add::i32 ... bench: 68 ns/iter (+/- 9)
test add::i64 ... bench: 70 ns/iter (+/- 7)
test add::i8 ... bench: 85 ns/iter (+/- 2)
test add::isize ... bench: 70 ns/iter (+/- 4)
test add::u128 ... bench: 88 ns/iter (+/- 3)
test add::u16 ... bench: 85 ns/iter (+/- 4)
test add::u32 ... bench: 67 ns/iter (+/- 3)
test add::u64 ... bench: 70 ns/iter (+/- 8)
test add::u8 ... bench: 85 ns/iter (+/- 3)
test add::usize ... bench: 70 ns/iter (+/- 4)
test mul::i128 ... bench: 58 ns/iter (+/- 3)
test mul::i16 ... bench: 29 ns/iter (+/- 1)
test mul::i32 ... bench: 29 ns/iter (+/- 1)
test mul::i64 ... bench: 52 ns/iter (+/- 3)
test mul::i8 ... bench: 30 ns/iter (+/- 2)
test mul::isize ... bench: 52 ns/iter (+/- 3)
test mul::u128 ... bench: 58 ns/iter (+/- 6)
test mul::u16 ... bench: 29 ns/iter (+/- 2)
test mul::u32 ... bench: 29 ns/iter (+/- 0)
test mul::u64 ... bench: 53 ns/iter (+/- 2)
test mul::u8 ... bench: 30 ns/iter (+/- 3)
test mul::usize ... bench: 53 ns/iter (+/- 2)
test rem::i128 ... bench: 9,913 ns/iter (+/- 680)
test rem::i16 ... bench: 2,923 ns/iter (+/- 151)
test rem::i32 ... bench: 1,214 ns/iter (+/- 125)
test rem::i64 ... bench: 3,652 ns/iter (+/- 200)
test rem::i8 ... bench: 1,179 ns/iter (+/- 51)
test rem::isize ... bench: 3,542 ns/iter (+/- 159)
test rem::u128 ... bench: 9,047 ns/iter (+/- 793)
test rem::u16 ... bench: 1,051 ns/iter (+/- 51)
test rem::u32 ... bench: 997 ns/iter (+/- 68)
test rem::u64 ... bench: 2,871 ns/iter (+/- 203)
test rem::u8 ... bench: 985 ns/iter (+/- 60)
test rem::usize ... bench: 2,946 ns/iter (+/- 276)
test sub::i128 ... bench: 32 ns/iter (+/- 2)
test sub::i16 ... bench: 17 ns/iter (+/- 1)
test sub::i32 ... bench: 18 ns/iter (+/- 1)
test sub::i64 ... bench: 17 ns/iter (+/- 1)
test sub::i8 ... bench: 16 ns/iter (+/- 1)
test sub::isize ... bench: 16 ns/iter (+/- 1)
test sub::u128 ... bench: 32 ns/iter (+/- 2)
test sub::u16 ... bench: 17 ns/iter (+/- 4)
test sub::u32 ... bench: 17 ns/iter (+/- 1)
test sub::u64 ... bench: 16 ns/iter (+/- 2)
test sub::u8 ... bench: 21 ns/iter (+/- 4)
test sub::usize ... bench: 16 ns/iter (+/- 4)
test result: ok. 0 passed; 0 failed; 0 ignored; 48 measured; 0 filtered out
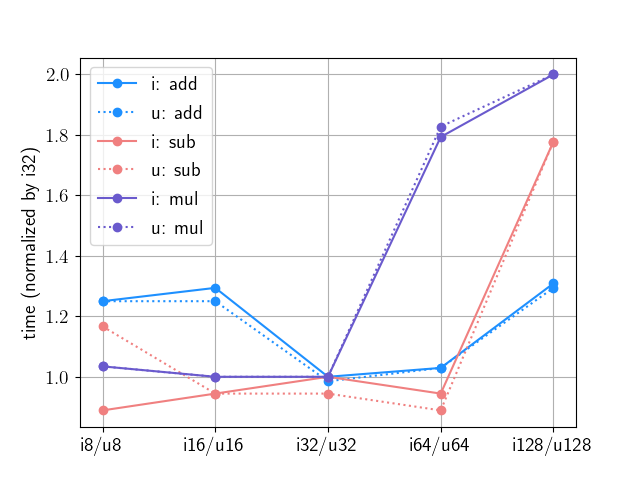
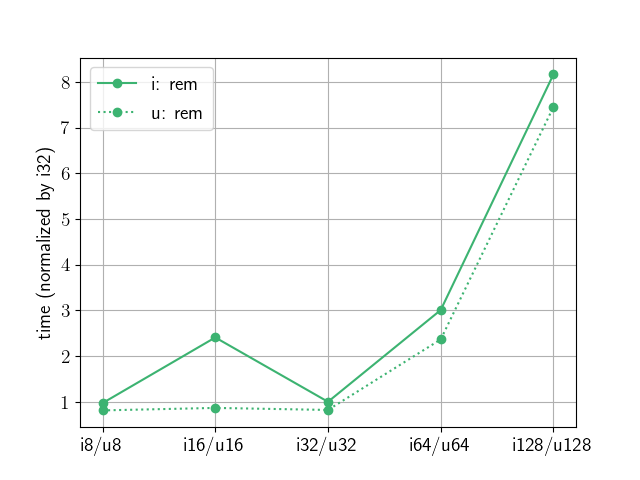
グラフにするとこんな感じです. 縦軸が計算に要した時間なので, 下に来るほど演算が速いことを意味します. 実線が符号あり, 点線が符号なしの結果です. なお縦軸は問題ごとに i32 の結果が 1 になるように規格化しています.
符号あり整数では i32 が演算の種類によらず安定して速いですね. 符号ありと符号なしでは bit 数が同じならほぼ同じか若干符号なしの方が速いのようです. 32 bit と 64 bit では積や剰余では 1.5 倍以上の差があるものの, 足し算/引き算だけならほぼ同等なのもおもしろいです.
アセンブリが読めて CPU アーキテクチャに通じていればもうちょっと深い考察ができるのかもしれませんが, そのスキルは持ってないのでこの記事はここで終わりです.