Rustの3種のべき乗演算の速度差について という記事の内容が驚き (powi より powf のが速い) だったので, 手元の環境でもベンチマークしてみました (環境については後述).
問題設定
元記事では $(-1)^n$ を計算していますが, 元記事で言及されている通りこれは普通 if 文を使って書くはずなので, 元記事の問題設定はあまり現実的ではないと思います. と言って Taylor 展開や多項式の計算などもべき乗を使わずに書くはずです.
そこでここでは次の和を計算するという問題を考えます.
$$S( x: T ) = \sum_{n = 0}^{127} n^x$$
ここに $T$ は変数 $x$ の型で, .pow() を用いるときは u32, .powi() を用いるときは i32, .powf() を用いるときは f64 です.
コード
長くなったので こちら に置いておきます (CC0).
なぜか bench_npow1 のみ最適化されてしまって計算時間が 0 になったので結果を標準出力することでそれを阻止しています. また最後の overhead というベンチマークは, イテレータの要素を f64 にキャストしていること, また浮動小数点数の和と整数の和を比較していること, によるオーバーヘッドの大きさを見るためのものです.
おまけとして, .powf(0.5) と .sqrt() の比較, べき乗をハードコードしたものも入っています.
結果
Debian 10.0 (WSL) on Win10 1903 (x86_64), Intel Core i7-6700 @3.40GHz で実行した結果です.
rustc 1.38.0-nightly (534b42394 2019-08-09)
running 11 tests
test bench_npow1 ... bench: 93 ns/iter (+/- 10)
test bench_npow2 ... bench: 159 ns/iter (+/- 23)
test bench_npow4 ... bench: 277 ns/iter (+/- 38)
test bench_npowf0_5 ... bench: 5,636 ns/iter (+/- 525)
test bench_npowf1 ... bench: 623 ns/iter (+/- 114)
test bench_npowf2 ... bench: 693 ns/iter (+/- 106)
test bench_npowf4 ... bench: 5,722 ns/iter (+/- 211)
test bench_npowi1 ... bench: 304 ns/iter (+/- 6)
test bench_npowi2 ... bench: 345 ns/iter (+/- 7)
test bench_npowi4 ... bench: 444 ns/iter (+/- 10)
test bench_nsqrt ... bench: 210 ns/iter (+/- 10)
test bench_ntimes2 ... bench: 111 ns/iter (+/- 5)
test bench_ntimes4 ... bench: 125 ns/iter (+/- 4)
test overhead ... bench: 98 ns/iter (+/- 4)
test result: ok. 0 passed; 0 failed; 0 ignored; 11 measured; 0 filtered out
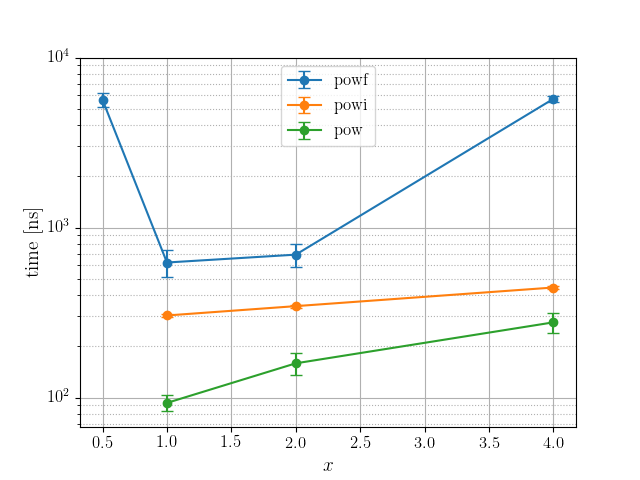
※縦軸が対数スケールになっています.
Win10 native の環境 (nightly-x86_64-pc-windows-msvc) でも試してみましたが, powf を除いてほぼ同じ数字でした. powf については
test bench_npowf0_5 ... bench: 3,976 ns/iter (+/- 387)
test bench_npowf1 ... bench: 438 ns/iter (+/- 19)
test bench_npowf2 ... bench: 3,984 ns/iter (+/- 427)
test bench_npowf4 ... bench: 3,980 ns/iter (+/- 388)
となっていて, .powf(4.) はネイティブの方が速いのに対して, .powf(2.) は .powf(4.) と同程度まで遅くなっています.
なお別のPC: Debian 9.9 (native), Intel Core i7-4790K CPU @4.00GHz でも実行しましたが, WSL での結果と定性的にはほぼ同じでした.
所感
pow が一番速くて powf が一番遅いという予想通りの結果になりました. 128回のべき乗を計算しているので, 1回のべき乗には最悪で 44 ns 程度かかっている見積もりですね.
いくつか試したんですが, 底が -1 のときに powf が異様に速いという元記事の結果を再現できませんでした. 元記事のベンチマークを試してみても
test benches::bench_leibniz_f64powf ... bench: 38,408,980 ns/iter (+/- 1,565,358)
test benches::bench_leibniz_f64powi ... bench: 33,490,600 ns/iter (+/- 917,164)
test benches::bench_leibniz_i64pow ... bench: 13,489,260 ns/iter (+/- 619,968)
で, powf が一番遅かったですし.
平方根 .sqrt() が圧倒的に速いのはともかく, べき乗をハードコードした bench_ntimes2, bench_ntimes4 が思ったよりだいぶ速かった (というか powi が遅かった) のが驚きです. もしかしたらハードコードした方は意図していない形まで最適化されていたのでしょうか?