やること
- ElasticNetを用いた多項式回帰
- 多項式回帰モデルよるの予測(プロット含む)
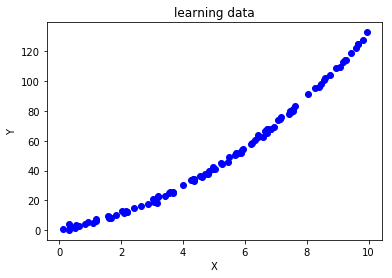
学習データ
データ生成に用いた式としては
y = 2x^2 + 3x + 1
にガウスノイズを加えたものを用いる。
学習データ数は100である。
予測用に用いたデータは同じ式を用いて新たに生成し,
50個用意した
xb2 = 10 * np.random.rand(100, 1)
yb2 = xb2**2 + 3.05*xb2 + 1.1 + np.random.randn(100,1)
plt.scatter(xb2,yb2,c = "b")
多項式回帰のための準備
データX(説明変数)の次元は1だが、データを観る限り、
2次多項式から生成されているっぽい。
sklearnのPolinomialFeaturesの機能を用いて、
元のデータを二乗したものを新たな特徴量として加える。
from sklearn.preprocessing import PolynomialFeatures as PF
pf = PF(degree=2, include_bias = False)
xb2_poly = pf.fit_transform(xb2)
Elastic-Netによる学習
今回使うモデルは、リッジ回帰、Lasso回帰等とならび、
基本的は学習で最小化すべきコスト関数に正則化項(制約)
を加えることで、過学習を防ぐ。
Elastic Netは、リッジ回帰とLasso回帰どちらにも用いられる
今回は単純なデータなので、2次多項式で回帰すべきだという判断がつけやすいが、
実際はより特徴量がもっと多いことが殆どなので、これは役立つ。
J(\theta) = MSE(θ) + r\alpha \sum_i^n|\theta_i| + \frac{1- r}{2} \alpha \sum_i^n \theta^2_i
\\
*MSE(\theta):最小二乗法誤差。
\\
制約を加えない場合によく用いられるコスト関数。
このElastic Netでは、パラメータとして、制約の程度を表すαと、
リッジ回帰、lasso回帰のどちらを重視すべきかを決めるrを
定める必要がある。これは、グリッドサーチなどを用いて、
実際にどのパラメータを用いた時に予測性能が良いかを探る必要がある。
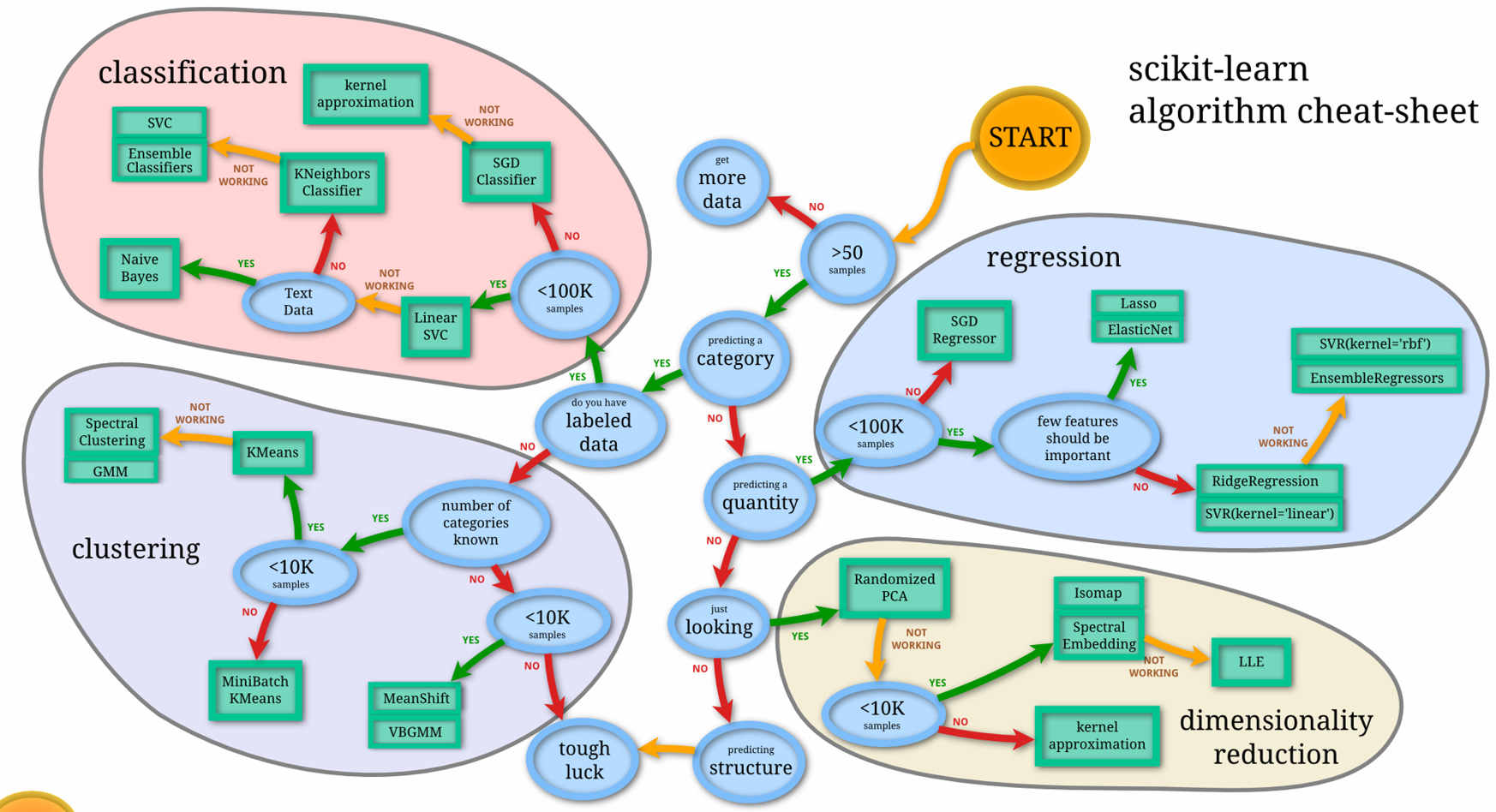
今回はElastic Netを用いたが、以下のチートシート等を用いて、
どのモデルを用いるべきかの判断を行う。
from sklearn.linear_model import ElasticNet
e_net = ElasticNet(alpha = 0.1, l1_ratio = 0.5)
e_net.fit(xb2_poly, yb2)
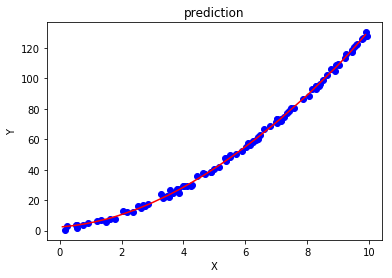
予測
あとは、前述した予測用データを用いて予測を行う。
この際、numpyのソート等を用いて、説明変数の順番を昇順にしておく必要がある。
xb2_t = 10* np.random.rand(50, 1)
print("xb2_t\n",xb2_t.shape)
# np.sortの使い方注意
xb2_t = np.array([np.sort(xb2_t[:,0])]).reshape(50,1)
print("xb2_t after\n", xb2_t.shape)
xb2t_poly = pf.fit_transform(xb2_t)
yb2_pred = e_net.predict(xb2t_poly)
plt.scatter(xb2,yb2,color = "blue")
plt.plot(xb2_t,yb2_pred,"red")
plt.show()
参考
scikit-learnとTensorFlowによる実践機械学習
Aurélien Géron 著、下田 倫大 監訳、長尾 高弘 訳
https://www.oreilly.co.jp/books/9784873118345/