PSOの特徴

PSOは，粒子群最適化(Particle Swarm Optimization)の略語で，生物の行動を参考にして提案された群知能最適化手法の一種[参考1]．複数の粒子(生物個体)を探索のために利用し，各個体が最適化を行った際に得られる知見を基にして最適値を探索する手法．アルゴリズムの簡便さと最適化性能の高さから，様々な分野での活用が報告されています．例えば，制御の分野だとPID制御のゲインチューニング[参考2]やシステム同定などに使われているようです[参考3].

PSOのアルゴリズム

粒子群最適化(PSO)のアルゴリズムを以下に示します．ステップ1~4について章割りして説明していこうと思います．
$k$は粒子番号を示すインデックス，$t$はイタレーションを示すインデックス，$X_k(t)$は$k$番目の粒子の$t$における位置，$V_k(t)$は$k$番目の粒子の$t$における速度を表しています．また，$X_k^{pbest}(t)$は$k$番目の粒子の$t$イタレーションまでの間で最も良い粒子位置，$X^{gbest}(t)$は全粒子の内で$t$イタレーションまでで最適な値，$w,c_1,c_2(>0)$は正の値を取る重み，$r_1,r_2$は乱数(0から1の間で一様乱数で取得するなど)となります．　
1. 初期化($t\leftarrow 0$)
$$X_k(0), V_k(0) $$
2. 位置更新
$$X_k(t+1) = X_k(t) + V_k(t)$$
3. 速度更新
$$V_k(t+1) = wV_k(t) + c_1r_1\left(X_k^{pbest}(t)-X_k(t+1) \right)+ c_2r_2\left(X^{gbest}(t)-X_k(t+1) \right)$$
4. 最適値$X_k^{pbest}(t)，X_k^{gbest}(t)$の更新，終了判定($t\leftarrow t+1$)

1.初期化

全ての粒子(インデックス:$k=1,\ldots ,n$)に対して，粒子の初期位置$X_k(0)$と初期速度$V_k(0) $を与える．初期解を真の解の近くに取ることが出来れば収束が早くなることは容易に想像できるので，初期解の与え方は最適化の一つの重要なポイントになりますが，有効な初期解の与え方は一般には不明なので，一様乱数で与えるのが一般的だと思います．

2.位置更新

$$X_k(t+1) = X_k(t) + V_k(t)$$
このステップでは，速度を用いて粒子の位置を更新する．この粒子の位置こそが最適化問題の解の候補となるので，次のステップで説明する粒子の速度の与え方がPSOの最適化方針の肝となります．

3.速度更新

$$V_k(t+1) = wV_k(t) + c_1r_1\left(X_k^{pbest}(t)-X_k(t+1) \right)+ c_2r_2\left(X^{gbest}(t)-X_k(t+1) \right)$$
PSOの更新式の肝となる速度更新は上式で与えられる．この式の要約は，3つのベクトルの線形和で速度を更新するというものです．したがって，探索する方向を決めるベクトルの与え方が重要となります．以下，各項(ベクトル)の意味について説明したいと思います．

$wV_k(t)$：慣性方向の速度
前ステップで利用された速度ベクトルの方向に進むためのベクトル
$c_1r_1\left(X_k^{pbest}(t)-X_k(t+1) \right)$：
$k$番目の粒子の，$t$イタレーションまでの内の最適解の方向へ進むためのベクトル
$c_2r_2\left(X^{gbest}(t)-X_k(t+1) \right)$：
全粒子の内で，$t$イタレーションまでの最適解の方向へ進むためのベクトル

PSOの実装

PSOのアルゴリズムをpythonで実装してみました．

目的関数の設定
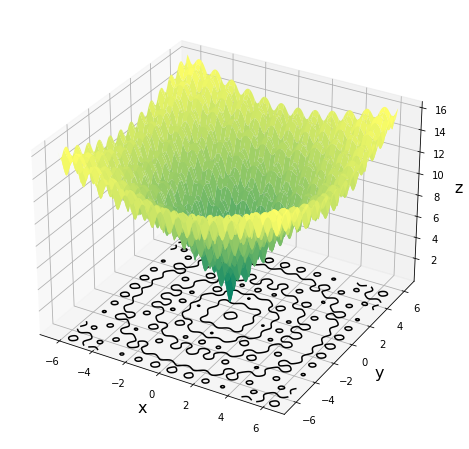
まずは，目的関数として以下のAckley functionと呼ばれる関数を最適化してみることにしました．勾配法だと局所解にスタックしそうな非凸な目的関数です．目的関数として他の関数を設定しても大丈夫なので，最適化アルゴリズムを評価するベンチマーク関数まとめなどを参考にして色々遊んでみると楽しいと思います．

objective_function.ipynb

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 目的関数
def objective_function(X,Y):
    t1 = 20
    t2 = -20 * np.exp(-0.2 * np.sqrt(1.0 / 2 * (X**2 + Y**2 )))
    t3 = np.e
    t4 = -np.exp(1.0 / 2 * (np.cos(2 * np.pi * X)+np.cos(2 * np.pi * Y)))
    return t1 + t2 + t3 + t4

# Figureと3DAxeS
fig = plt.figure(figsize = (8, 8))
ax = fig.add_subplot(111, projection="3d")

# 軸ラベルを設定
ax.set_xlabel("x", size = 16)
ax.set_ylabel("y", size = 16)
ax.set_zlabel("z", size = 16)

# 円周率の定義
pi = np.pi

# (x,y)データを作成
x = np.linspace(-2*pi, 2*pi, 256)
y = np.linspace(-2*pi, 2*pi, 256)

# 格子点を作成
X_p, Y_p = np.meshgrid(x, y)
Z = objective_function(X_p,Y_p)

# # 曲面を描画
ax.plot_surface(X_p, Y_p, Z, cmap = "summer")

# # 底面に等高線を描画
ax.contour(X_p, Y_p, Z, colors = "black", offset = -1)

plt.show()

PSOの実装
この目的関数に対して，PSOを適用する．PSOのプログラムを以下に示します．今回は，粒子を100個，終了条件を1000イタレーションとしました．

Particle_Swarm_Optimization.ipynb

fig = plt.figure()
ax = fig.add_subplot(projection='3d')

#初期化
N = 100 #粒子数
max_iter = 1000
X = 6*np.random.rand(2, N) - 3*np.ones((2, N)) 
V = 0.2*np.random.rand(2, N) - 0.1*np.ones((2, N))
Z_plain = np.zeros((1,N))
pbest = np.zeros((3,N))
pbest[0:2,:] = X
Zinit = objective_function(pbest[0,:],pbest[1,:]) 
pbest[2,:] = Zinit
#初期化した粒子の内で最も良いものをgbestとして格納
ap = np.argmin(Zinit)
gbest = np.array([pbest[0,ap],pbest[1,ap],objective_function(pbest[0,ap],pbest[1,ap])])

w = 0.1
c1 = 0.01
c2 = 0.01
res = np.zeros((2,max_iter))
for i in range(max_iter):
  # N個分の粒子をfor文で計算
  for j in range(N):
    #位置の更新
    X[:,j] = X[:,j] + V[:,j]
    #速度の更新
    V[:,j] = w*V[:,j] + c1*np.random.rand(1)*(pbest[0:2,j]-X[:,j]) +c2*np.random.rand(1)*(gbest[0:2]-X[:,j])
    if  objective_function(X[0,j],X[1,j]) < pbest[2,j]:
       pbest[0:2,j] = X[:,j]
       pbest[2,j] = objective_function(X[0,j],X[1,j])
  # N個の粒子の内で最適なものを取得し，過去の最適値と比較する
　a = np.argmin(pbest[2,:])
  if pbest[2,a] < gbest[2]:
    gbest[0:2] = pbest[0:2,a]
    gbest[2] = objective_function(gbest[0],gbest[1])
  
  #イタレーション回数iとその際の最適値を格納
  res[:,i] = np.array([i,gbest[2]])
  if np.mod(i,100) == 0:
    plt.plot(res[0,0:i],res[1,0:i])
    plt.show()


plt.plot(res[0,:],res[1,:])
print(gbest)

数値結果
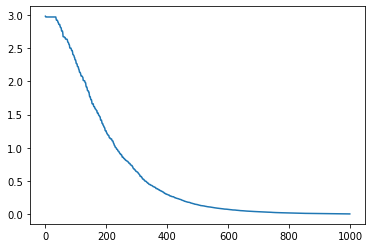
結果として，以下のような結果となりました．決定変数$x,y$が十分ゼロに近づいていることがわかるかと思います．

#x y zの値
[-1.19319988e-16 -3.71021410e-16  0.00000000e+00]

横軸をイタレーション，縦軸を評価値の値を示す．単調に下がっていくことが確認できたと思います．

まとめ

最適化手法であるPSOについて解説してみました．このアルゴリズムだと勾配が取得できない(=目的関数の形が陽に分からない)場合でも，入力(=決定変数の値)を入れて出力(=評価値)が出てくれば実装できるので，汎用性が高いです．ぜひ，プログラムを触ってみていただければと思います．

粒子群最適化(PSO:Particle Swarm Optimization)