More than 5 years have passed since last update.

TIS株式会社

JavaFXで振り返る高校物理（力学）

Last updated at 2015-09-01Posted at 2015-08-16

高校の教科で最も面白い物理を、 JavaFX で振り返る。

力学をプログラミングする実装はよく見るけど、オブジェクト指向を意識した実装はあまり見ない気がするので、その辺も意識しつつ。。。

ソースは GitHub に上げてます。

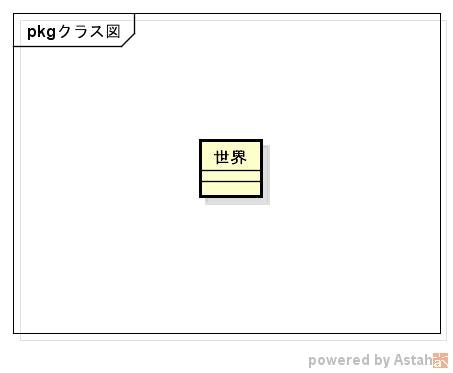
#まずは世界を作る
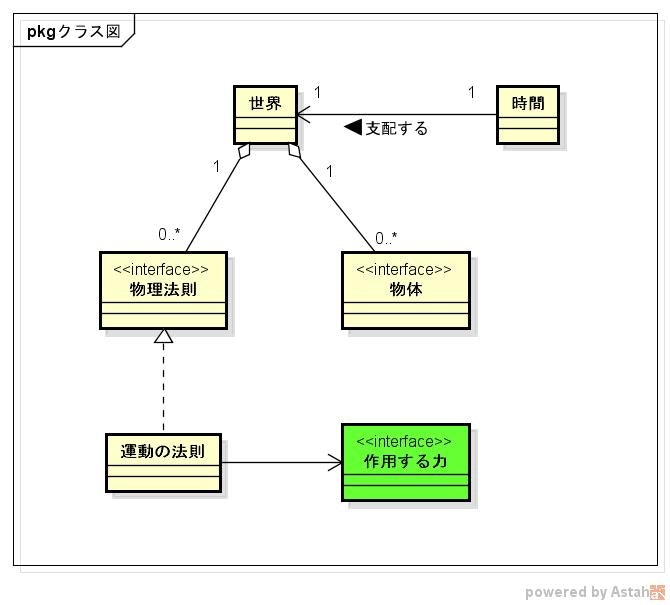
物理を学ぶ前に、まずは物理学の対象であるこの世界をモデリングし、実装しておく。

##モデリング

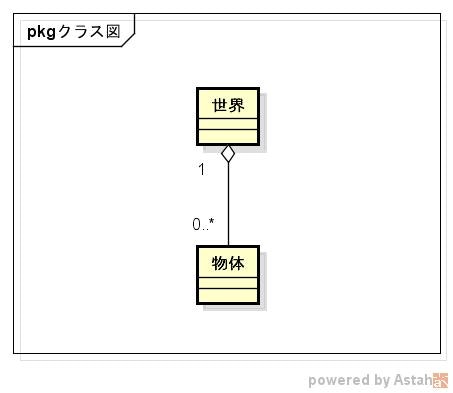
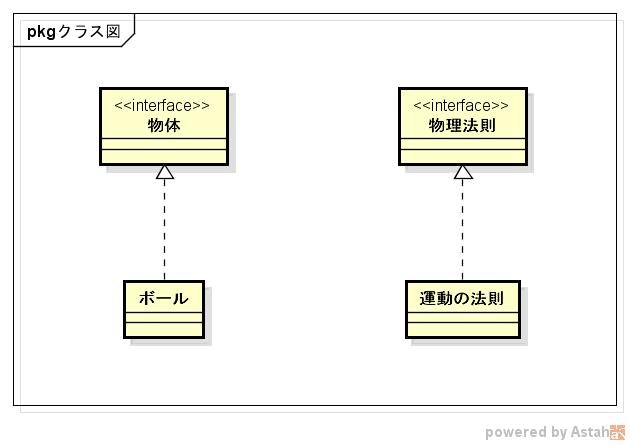
まず、「世界」がある。

「世界」には、「物体」がたくさん含まれる。

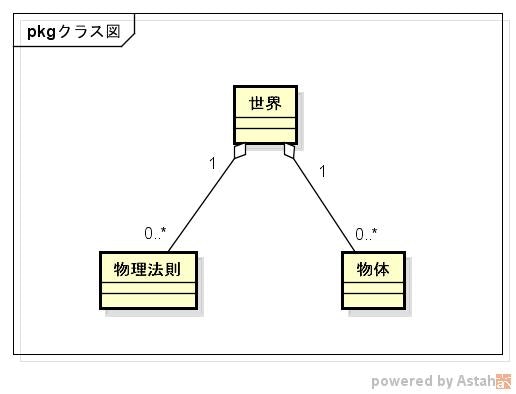
また、「世界」には「物理法則」が存在する。

「物理法則」は１つに統一されるかもしれないけど、まだ分からないのでとりあえず複数ある前提で進める。

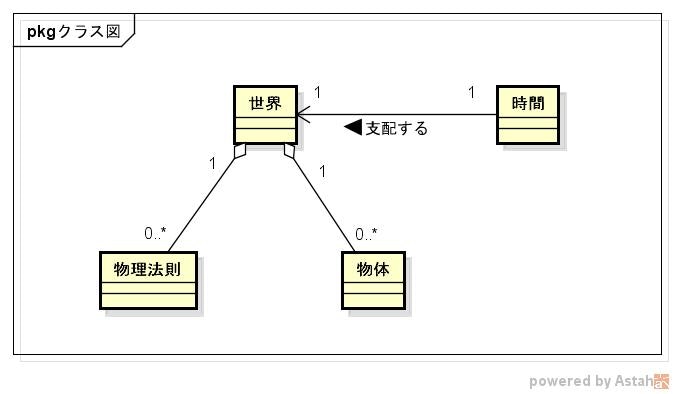
物理学における重要な概念として、「時間」がある。

「時間」は「世界」に含まれるというよりかは、「時間」が「世界」を支配している気がするので、こんな感じで。

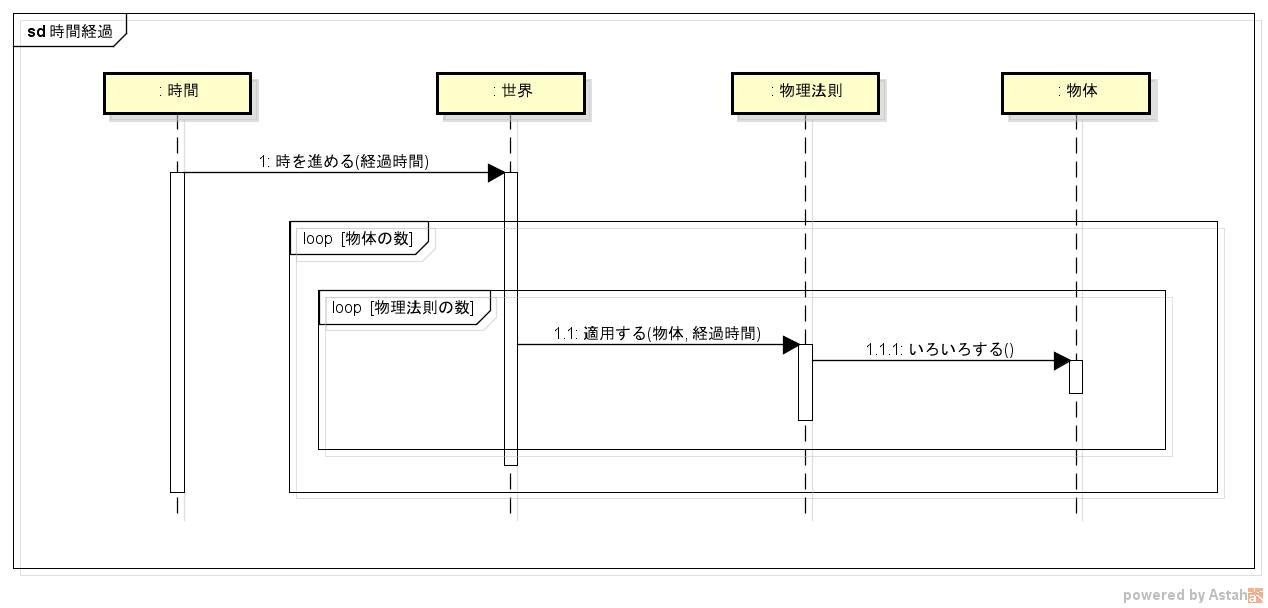
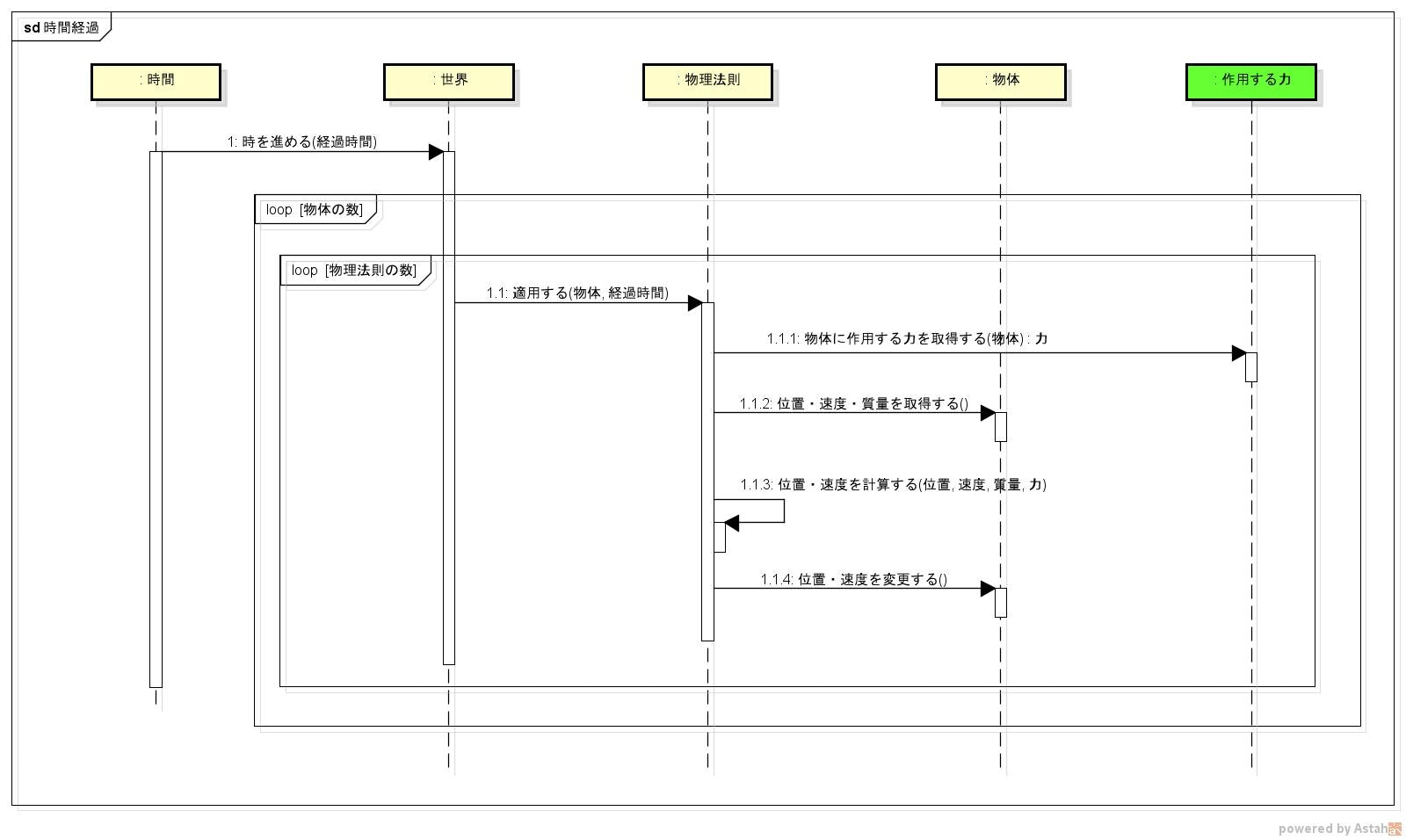
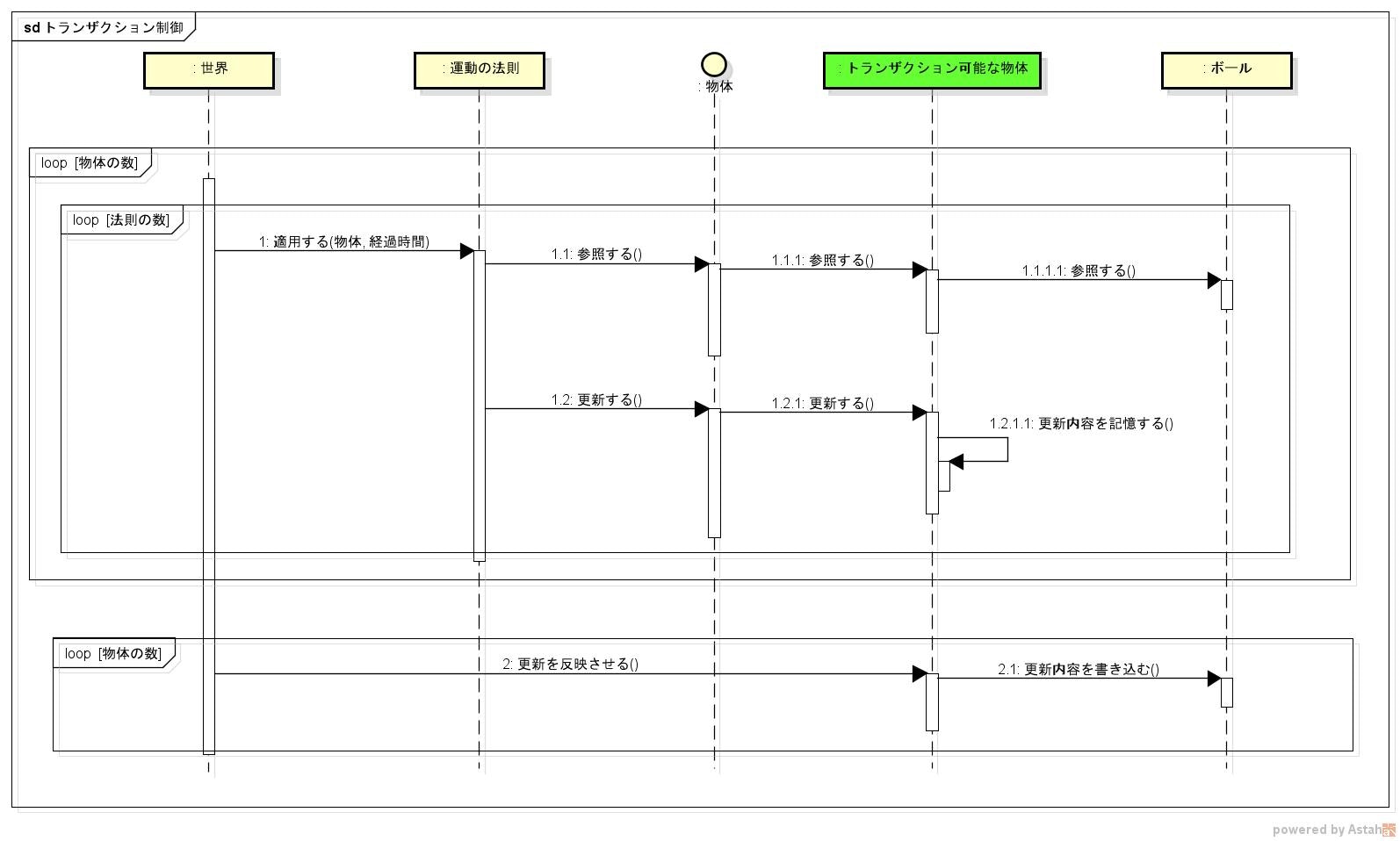
このモデルが表す「世界」の時間経過をシーケンス図にしてみる。

「時間」が「世界」に時間経過を通知し、「世界」が全ての「物体」に対して「物理法則」を適用していく感じ。

##実装
とりあえず実装する。

物体

Physical.java

package gl8080.physics.domain;

public interface Physical {
}

「物体」を英語に直訳すると object になる。しかし、これだと Java の Object クラスと名前が被るのでよろしくない。
また、具体的な物体が何なのかはまだ決まってないので interface で定義し、名前も Physical （物質界の）という形容詞にしておく。

物理法則

PhysicalLaw.java

package gl8080.physics.domain;

public interface PhysicalLaw {
    void apply(Physical physical, double t);
}

こちらも、まだ具体的な法則が分かっていないので、とりあえずインターフェースで作っておく。
apply() メソッドは、シーケンス図にあるのをそのまま起こした。

世界

World.java

package gl8080.physics.domain;

import java.util.HashSet;
import java.util.Objects;
import java.util.Set;

public class World {
    
    private Set<Physical> physicals = new HashSet<>();
    private Set<PhysicalLaw> physicalLaws = new HashSet<>();
    
    void next(double sec) {
        this.physicals.forEach(physical -> {
            this.physicalLaws.forEach(law -> {
                law.apply(physical, sec);
            });
        });
    }
    
    public void addPhysical(Physical physical) {
        Objects.requireNonNull(physical);
        this.physicals.add(physical);
    }
    
    public void addPhysicalLaws(PhysicalLaw law) {
        Objects.requireNonNull(law);
        this.physicalLaws.add(law);
    }
}

こちらもシーケンス図をそのまま実装した感じ。
next() メソッドはたぶん「時間」クラスからしか呼ばれないはずなので、パッケージプライベートにしている。

時間

Timer

package gl8080.physics.domain;

import java.util.Objects;

public class Time {

    private static final double FRAME_LATE = 1.0 / 30.0;

    private final World world;
    
    public Time(World world) {
        Objects.requireNonNull(world);
        this.world = world;
    }
    
    public void start() {
        while (true) {
            this.world.next(FRAME_LATE);
            this.sleep(FRAME_LATE);
        }
    }

    private void sleep(double sec) {
        try {
            Thread.sleep((long)(sec * 1000));
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
    }
}

start() で時間経過がスタートする。

無限ループをしながら、都度 1/30 秒間スリープしている。この 1/30 秒は、フレームレートを表していて、１秒間に３０回再描画を行うことになる。フレームレートは、値が大きすぎると動きがカクカクして不自然に感じてしまうが、 1/30 くらいにしておけば人間の目では不自然さを感じなくなる。

##お試し実装
この実装でうまく動くか、とりあえずダミーの「物体」と「物理法則」を用意して動かしてみる。

ダミー物体

DummyObject.java

package gl8080.physics.domain.dummy;

import gl8080.physics.domain.Physical;

public class DummyObject implements Physical {
    
    @Override
    public String toString() {
        return "DummyObject!!";
    }
}

ダミー法則

DummyLaw.java

package gl8080.physics.domain.dummy;

import gl8080.physics.domain.Physical;
import gl8080.physics.domain.PhysicalLaw;

public class DummyLaw implements PhysicalLaw {
    
    private int i = 0;
    
    @Override
    public void apply(Physical physical, double t) {
        System.out.println((i++) + " : " + physical);
    }
}

Main 処理

Main.java

package gl8080.physics;

import gl8080.physics.domain.Time;
import gl8080.physics.domain.World;
import gl8080.physics.domain.dummy.DummyLaw;
import gl8080.physics.domain.dummy.DummyObject;

public class Main {
    
    public static void main(String[] args) {
        World world = new World();
        world.addPhysical(new DummyObject());
        world.addPhysicalLaws(new DummyLaw());
        
        Time time = new Time(world);
        time.start();
    }
}

実行結果

0 : DummyObject!!
1 : DummyObject!!
2 : DummyObject!!
3 : DummyObject!!
4 : DummyObject!!
:
:

いい感じで動いた。
問題なさそう。

#JavaFX で 3DCG
JavaFX を使えば、簡単に 3DCG を描画することができる。

##Hello World

Main.java

package sample.javafx;

import javafx.application.Application;
import javafx.scene.Group;
import javafx.scene.PerspectiveCamera;
import javafx.scene.Scene;
import javafx.scene.paint.Color;
import javafx.scene.paint.PhongMaterial;
import javafx.scene.shape.Sphere;
import javafx.stage.Stage;

public class Main extends Application {
    
    public static void main(String[] args) {
        launch(args);
    }
    
    @Override
    public void start(Stage primaryStage) throws Exception {
        // 球体を作成して
        Sphere sphere = new Sphere(1.0);
        sphere.setMaterial(new PhongMaterial(Color.RED));
        sphere.setTranslateZ(5.0);
        
        // シーングラフに追加
        Scene root = new Scene(new Group(sphere), 500, 500);
        
        // カメラを設定
        root.setCamera(new PerspectiveCamera(true));
        
        // ウィンドウを表示
        primaryStage.setScene(root);
        primaryStage.show();
    }

}

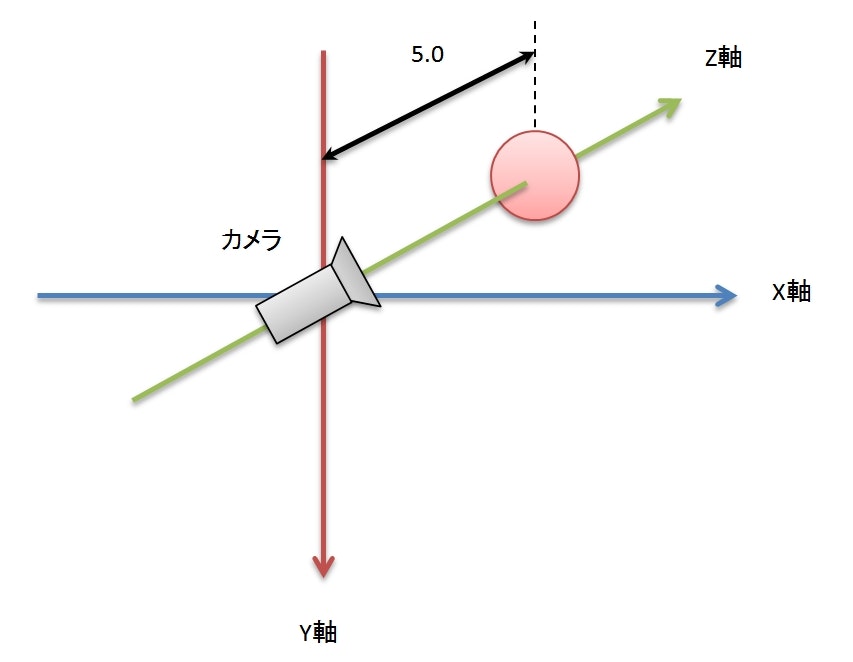
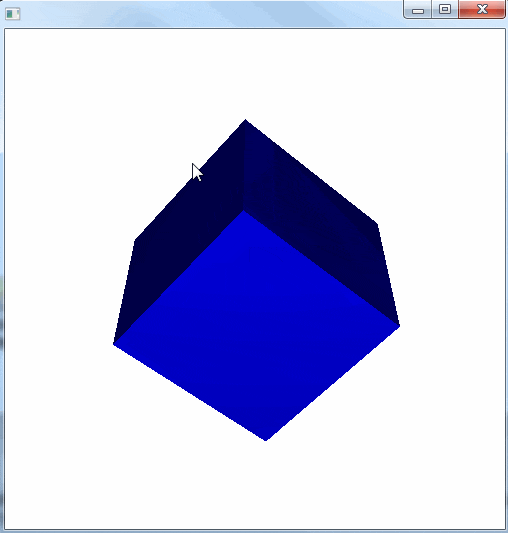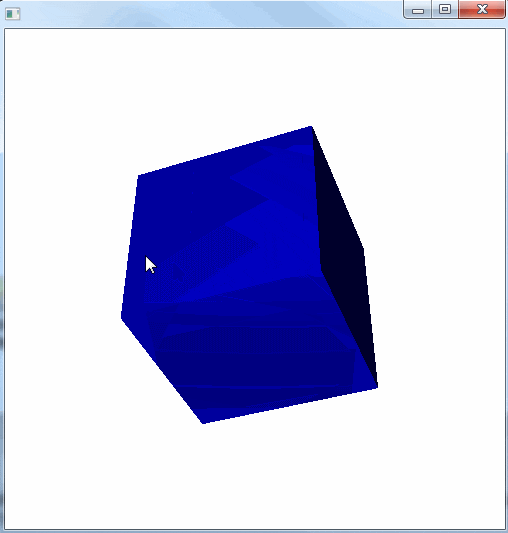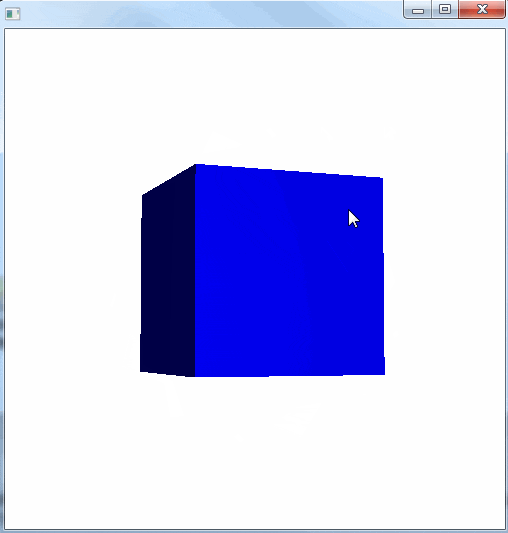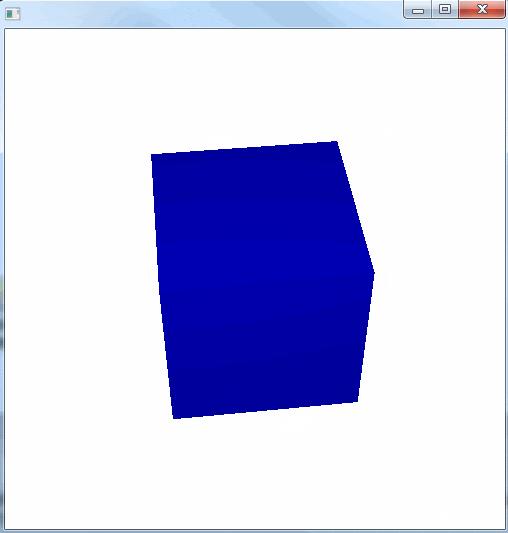
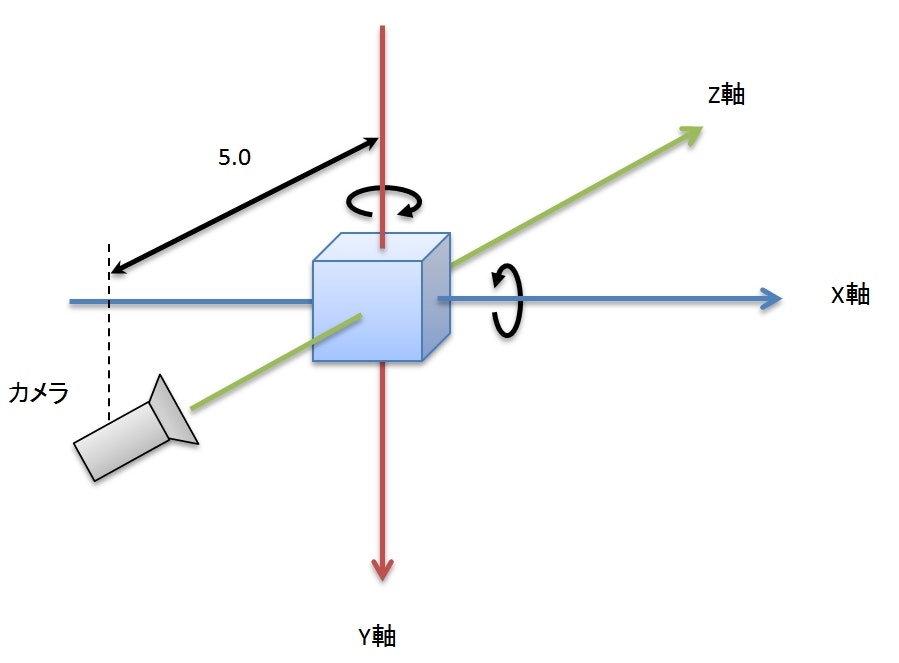
JavaFX で 3DCG を使いはじめるには、カメラ（PerspectiveCamera）をシーンに追加してあげればいい。

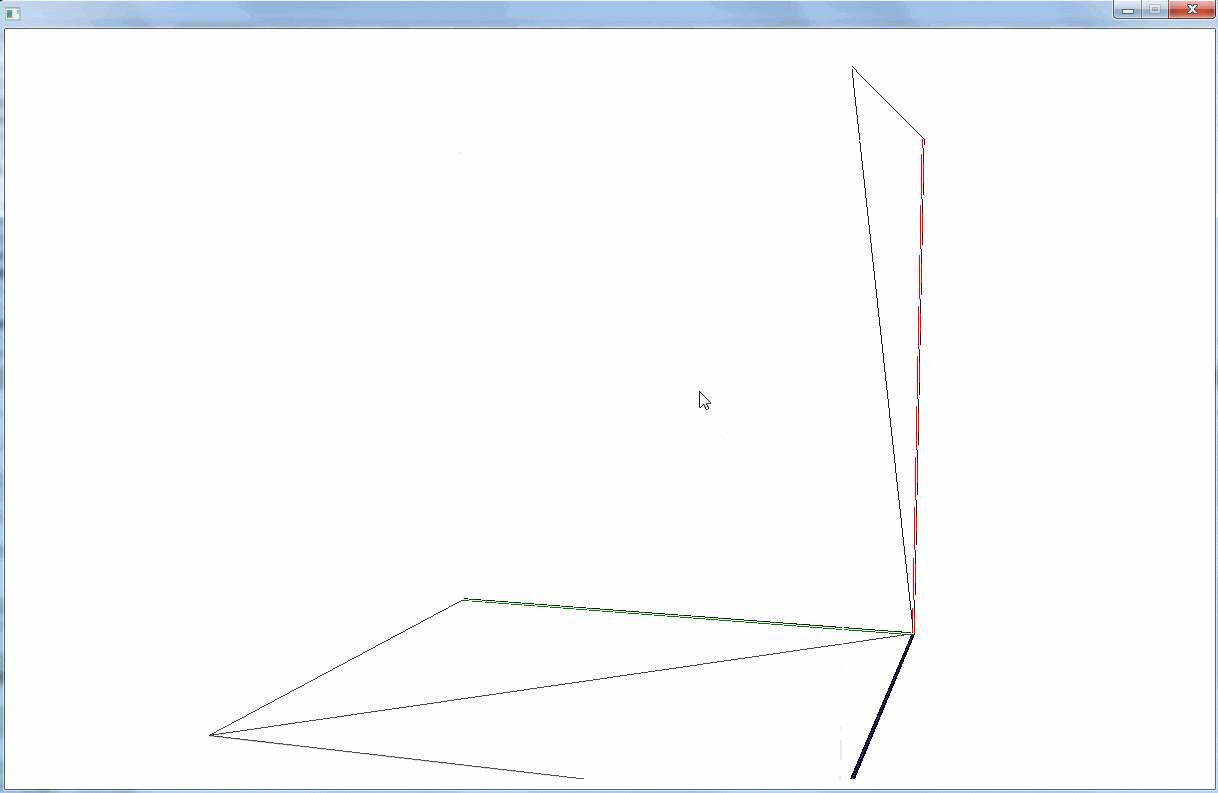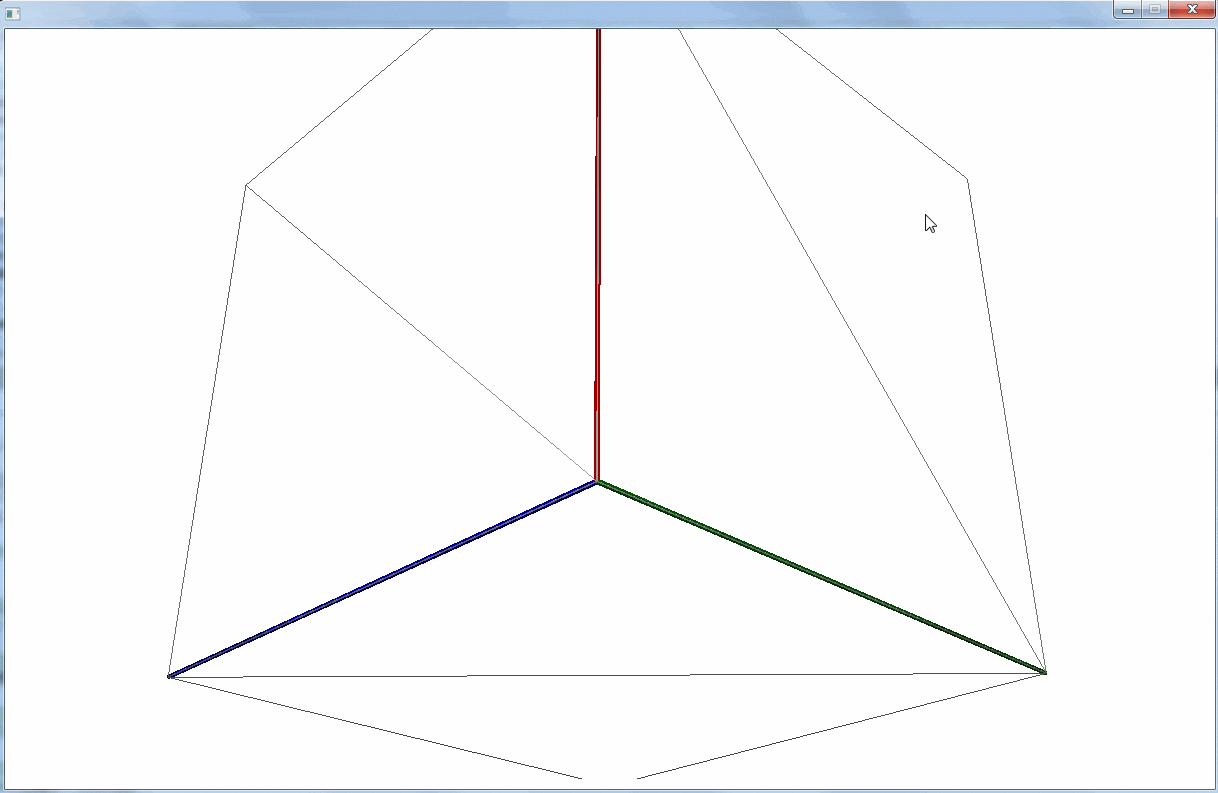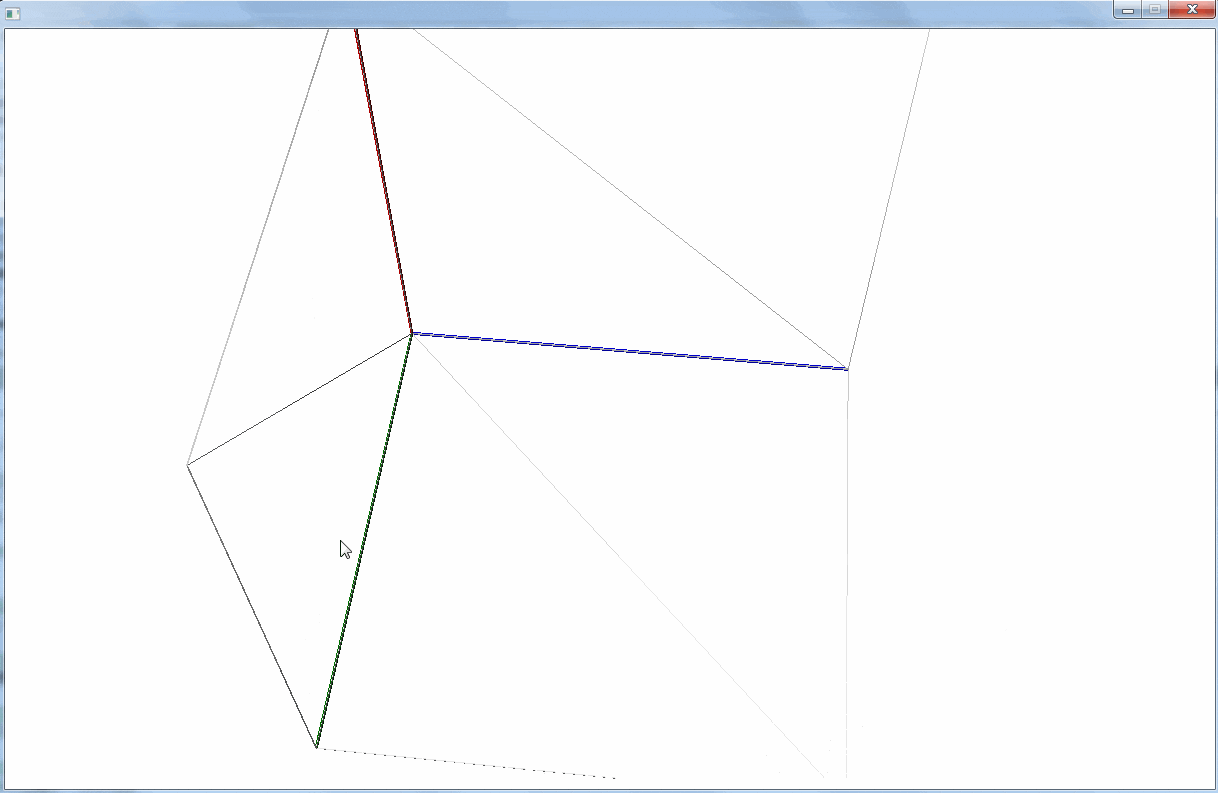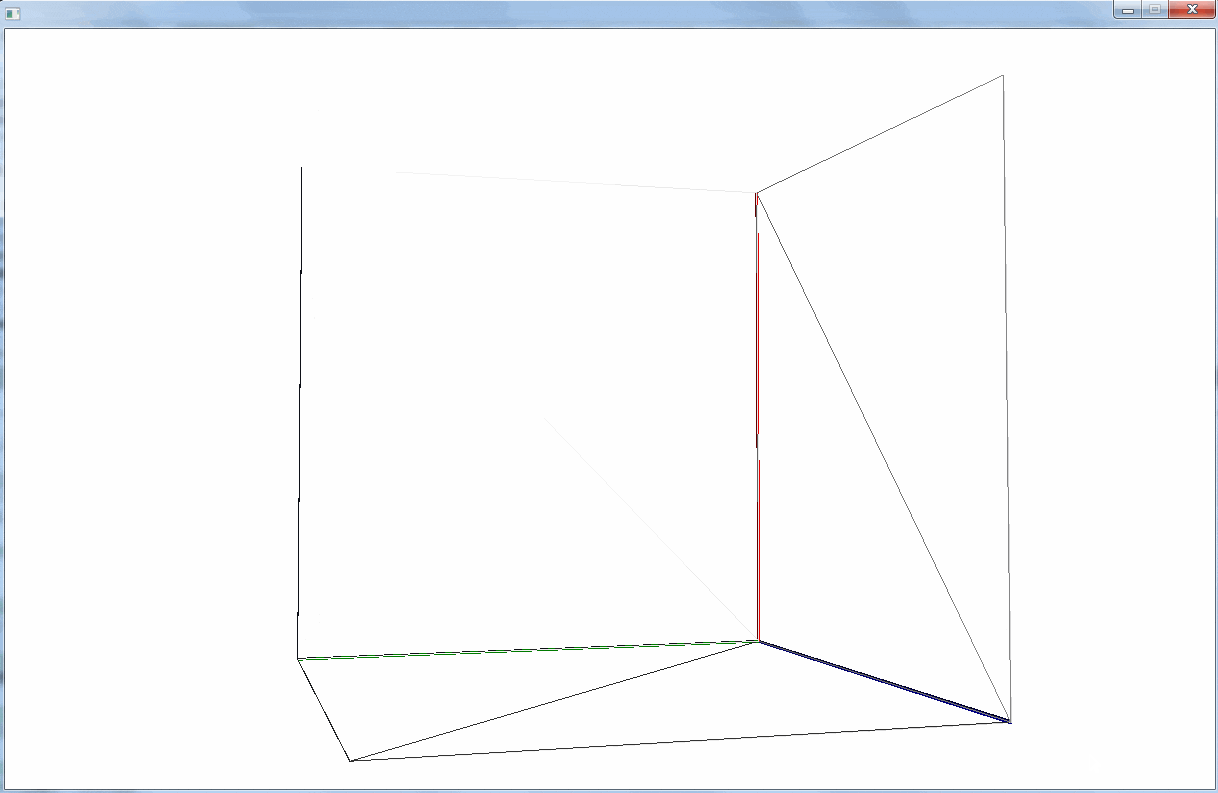
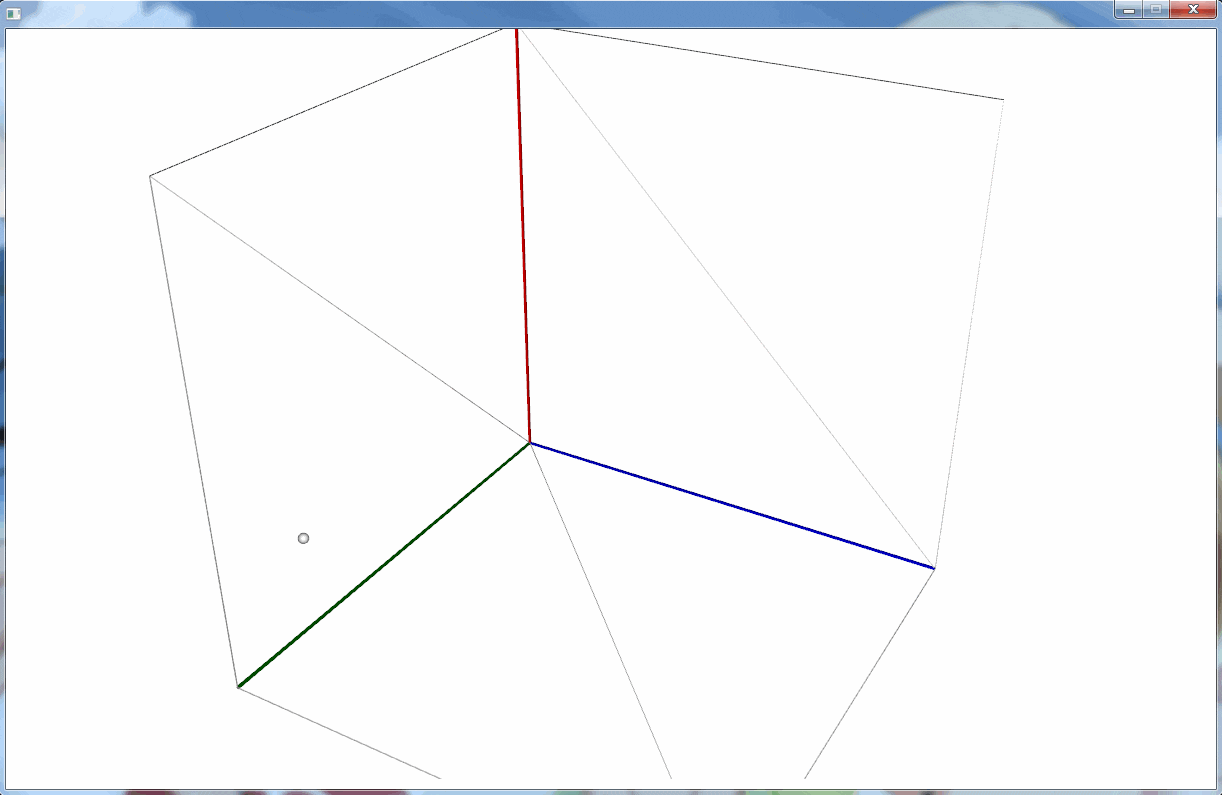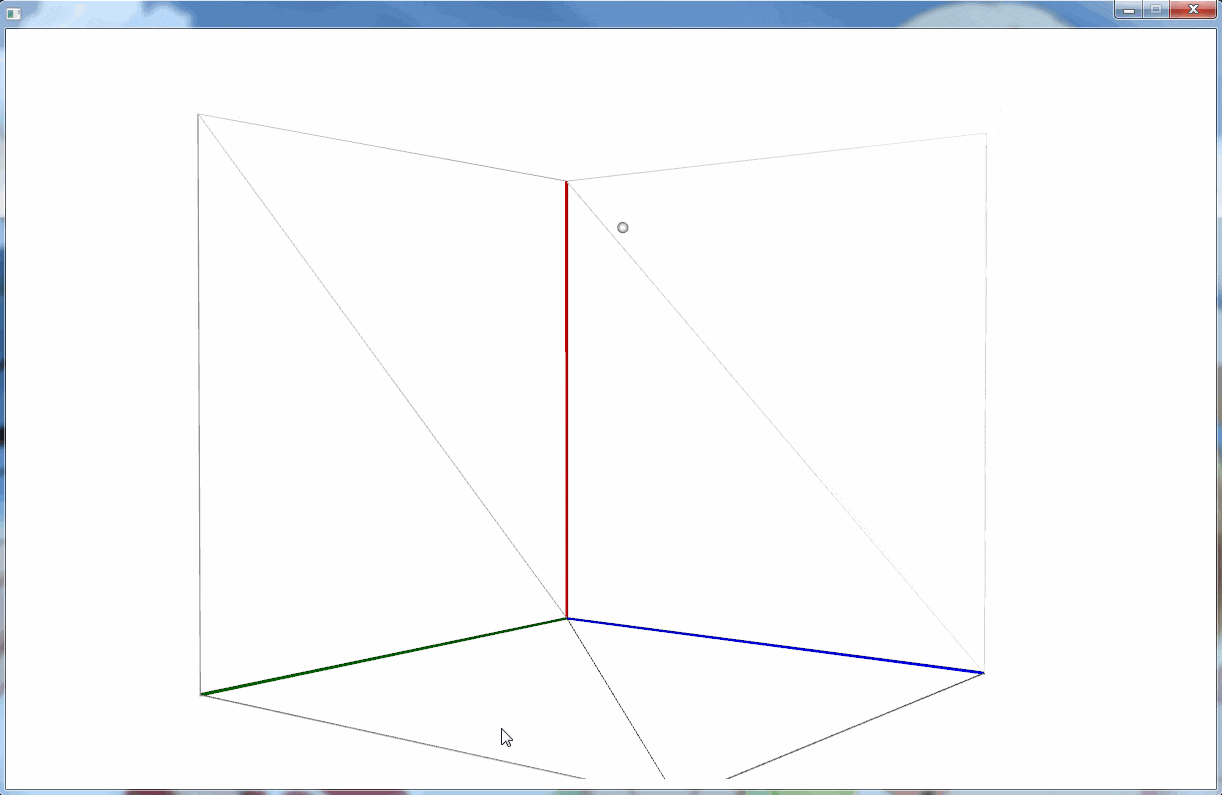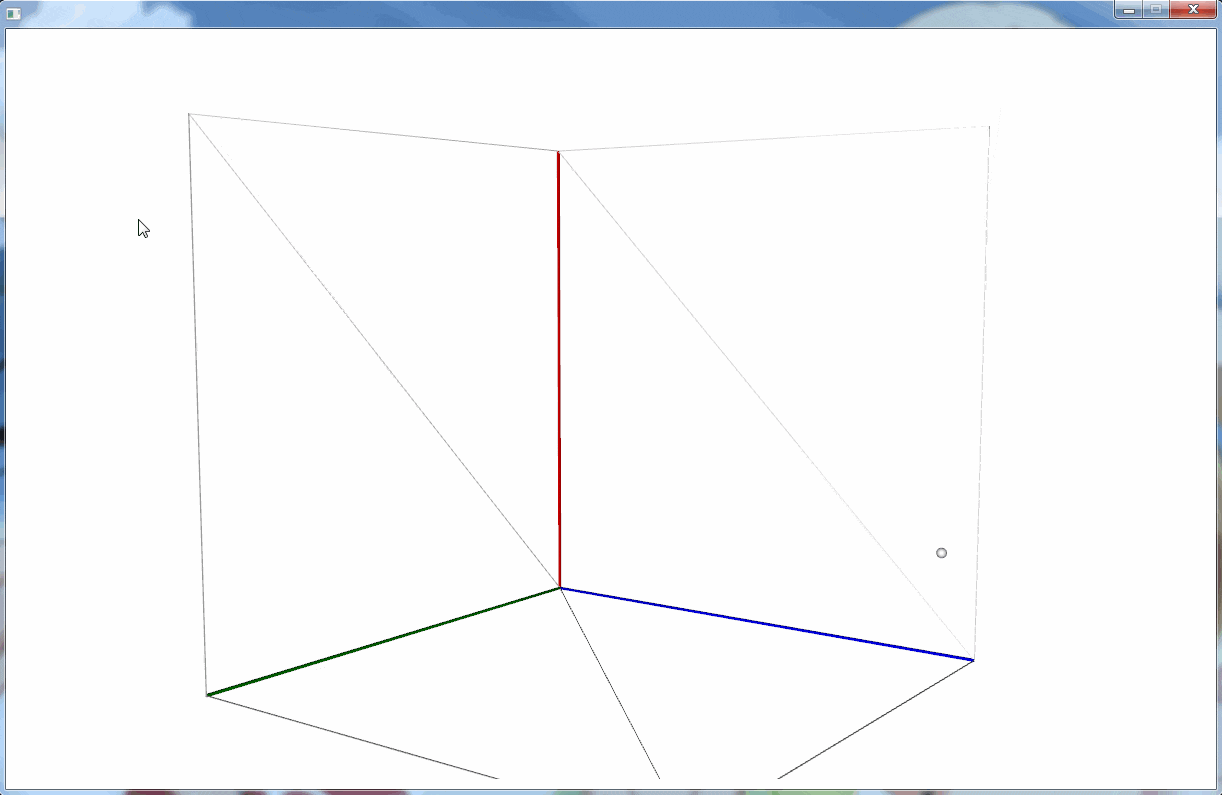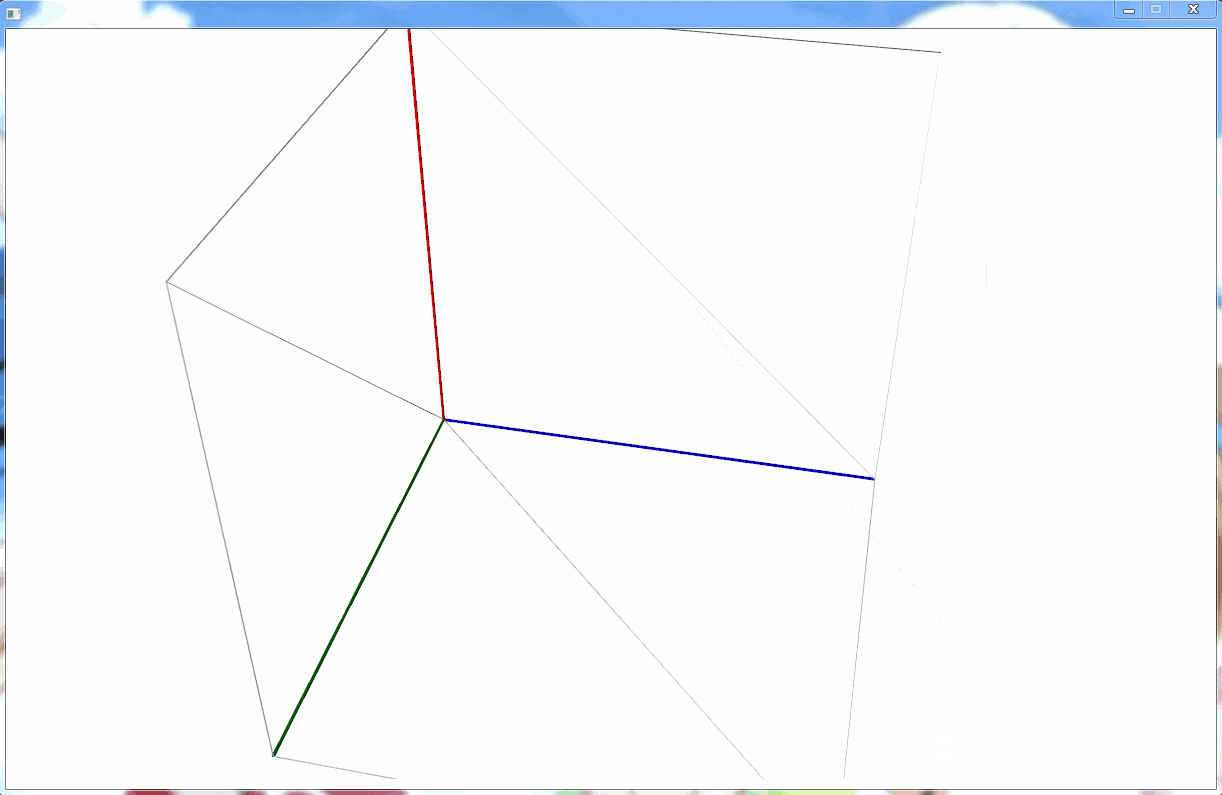
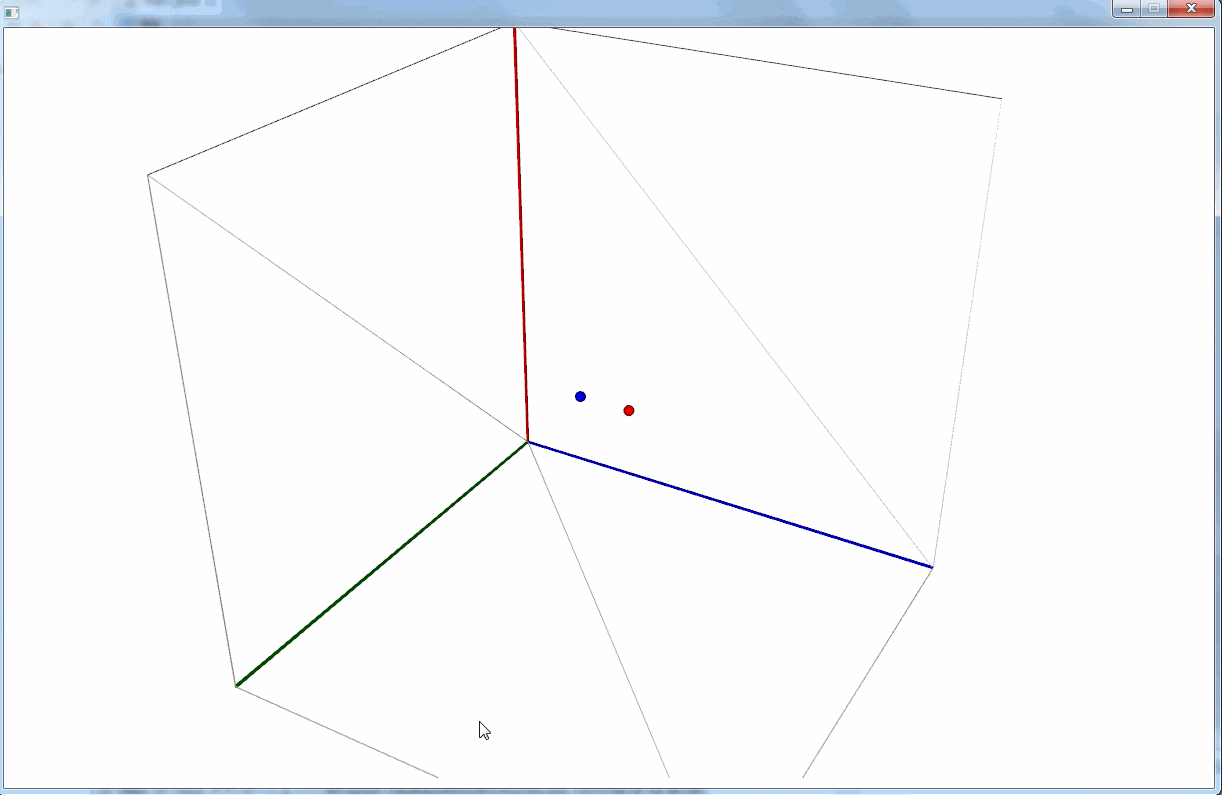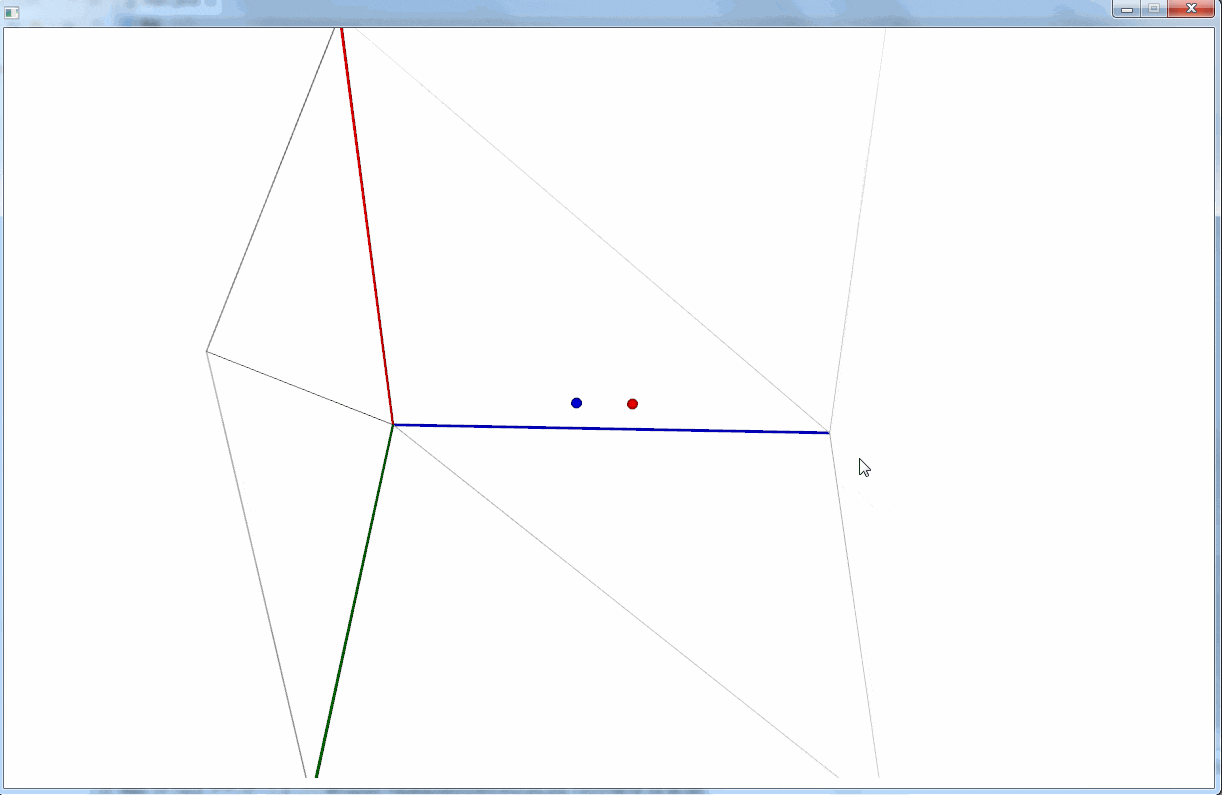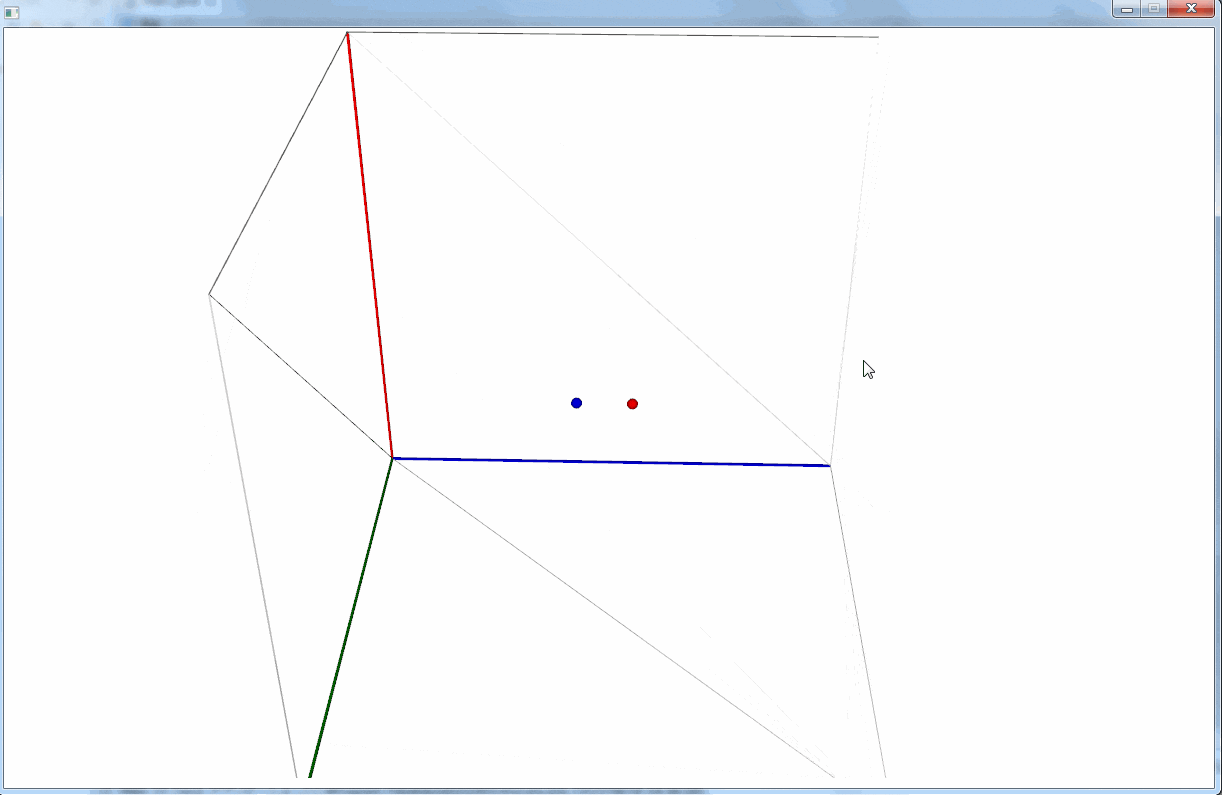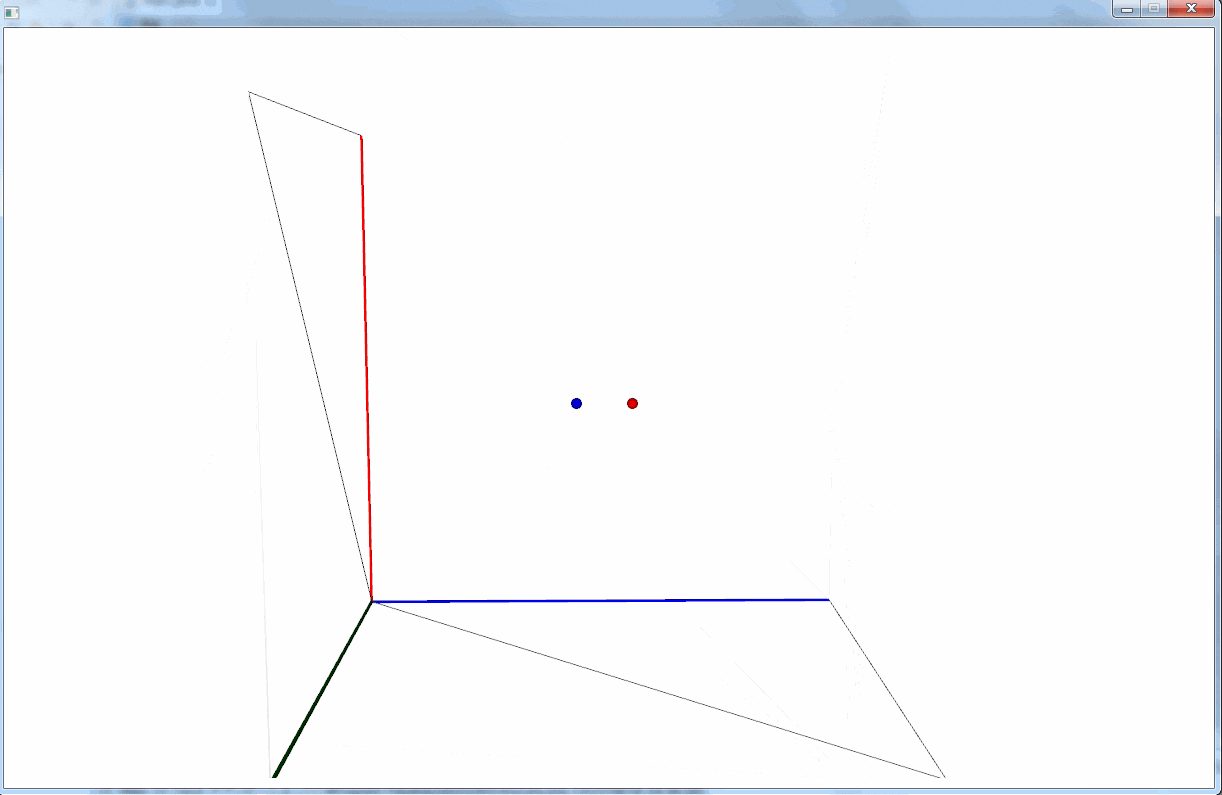
上記の実装は、次のような 3D 空間を定義していることになる。

半径 1.0 の球体を定義し、 Z軸上で +5.0 の位置に配置している。そして、カメラは原点から球体の方向（Z軸プラスの方向）を向いている。

JavaFX は OpenGL などの他の一般的な 3DCG ライブラリと異なり、 Y 軸がデフォルトで下向きになっている点に注意が必要（OpenGL などは上向き）。

##マウスでグリグリできるようにする
このままだと表示が固定されていて、 3DCG 感があまり得られない。
なので、マウスでグリグリ操作できるようにする。

Main.java

package sample.javafx;

import javafx.application.Application;
import javafx.scene.Group;
import javafx.scene.PerspectiveCamera;
import javafx.scene.Scene;
import javafx.scene.input.MouseEvent;
import javafx.scene.paint.Color;
import javafx.scene.paint.PhongMaterial;
import javafx.scene.shape.Box;
import javafx.scene.transform.Rotate;
import javafx.stage.Stage;

public class Main extends Application {
    
    public static void main(String[] args) {
        launch(args);
    }
    
    private double x;
    private double y;
    
    @Override
    public void start(Stage primaryStage) throws Exception {
        // 立方体を作成
        Box box = new Box(1.0, 1.0, 1.0);
        box.setMaterial(new PhongMaterial(Color.BLUE));
        
        Group group = new Group(box);
        
        // 立方体を含むグループを回転させるための Rotate を登録
        Rotate rotateX = new Rotate(0.0, Rotate.X_AXIS);
        Rotate rotateY = new Rotate(0.0, Rotate.Y_AXIS);
        group.getTransforms().addAll(rotateX, rotateY);
        
        // シーングラフに追加
        Scene root = new Scene(group, 500, 500);
        
        // マウスイベントのハンドラを登録
        root.addEventHandler(MouseEvent.MOUSE_PRESSED, e -> {
            // マウスがクリックされたときの位置を記録
            this.x = e.getSceneX();
            this.y = e.getSceneY();
        });
        
        root.addEventHandler(MouseEvent.MOUSE_DRAGGED, e -> {
            // ドラッグした距離に応じて、立方体を含むグループを回転させる
            double nowX = e.getSceneX();
            double nowY = e.getSceneY();
            
            double dx = this.x - nowX;
            double dy = this.y - nowY;
            
            // Y方向へのドラッグは、 X軸で回転させる
            rotateX.setAngle(rotateX.getAngle() - dy*0.5);
            // X方向へのドラッグは、 Y軸で回転させる
            rotateY.setAngle(rotateY.getAngle() + dx*0.5);
            
            this.x = nowX;
            this.y = nowY;
        });
        
        // カメラを設定
        PerspectiveCamera camera = new PerspectiveCamera(true);
        camera.setTranslateZ(-5.0);
        root.setCamera(camera);
        
        // ウィンドウを表示
        primaryStage.setScene(root);
        primaryStage.show();
    }

}

3D 空間は次のようになっている。

今度は原点に立方体を置いて、カメラの位置を後退させている。
立方体の回転は、カメラを動かすのではなく、立方体を含む Group を回転させることで実現している。

###JavaFX での座標変換

    @Override
    public void start(Stage primaryStage) throws Exception {
        // ...
        
        // 立方体を含むグループを回転させるための Rotate を登録
        Rotate rotateX = new Rotate(0.0, Rotate.X_AXIS);
        Rotate rotateY = new Rotate(0.0, Rotate.Y_AXIS);
        group.getTransforms().addAll(rotateX, rotateY);
        
        // ...
        
        root.addEventHandler(MouseEvent.MOUSE_DRAGGED, e -> {
            // ...
            
            rotateX.setAngle(rotateX.getAngle() - dy*0.5);
            rotateY.setAngle(rotateY.getAngle() + dx*0.5);

            // ...
        });

        // ...
    }

JavaFX で単純な座標変換を行うには、 setTranslateX() などの簡易メソッドを使う方法がある。

しかし、ある程度複雑な座標変換を行う場合は getTransforms() で取得できる ObservableList<Transform> に対して座標変換用のオブジェクトを渡す方法が必要になる。

クラス名が Observable* となっているように、ここに設定した座標変換のオブジェクトはプロパティの変更が監視されるようになる。
そして、プロパティが変更されれば表示に結果が自動で反映されるようになる。

##実験場を作る
上記の実装を基本に、物理実験用の空間を作る。

実装は長くなったので、 GitHub に上げているコードを参照のこと。
Y軸の向きは、分かりやすいように上向きにしている。

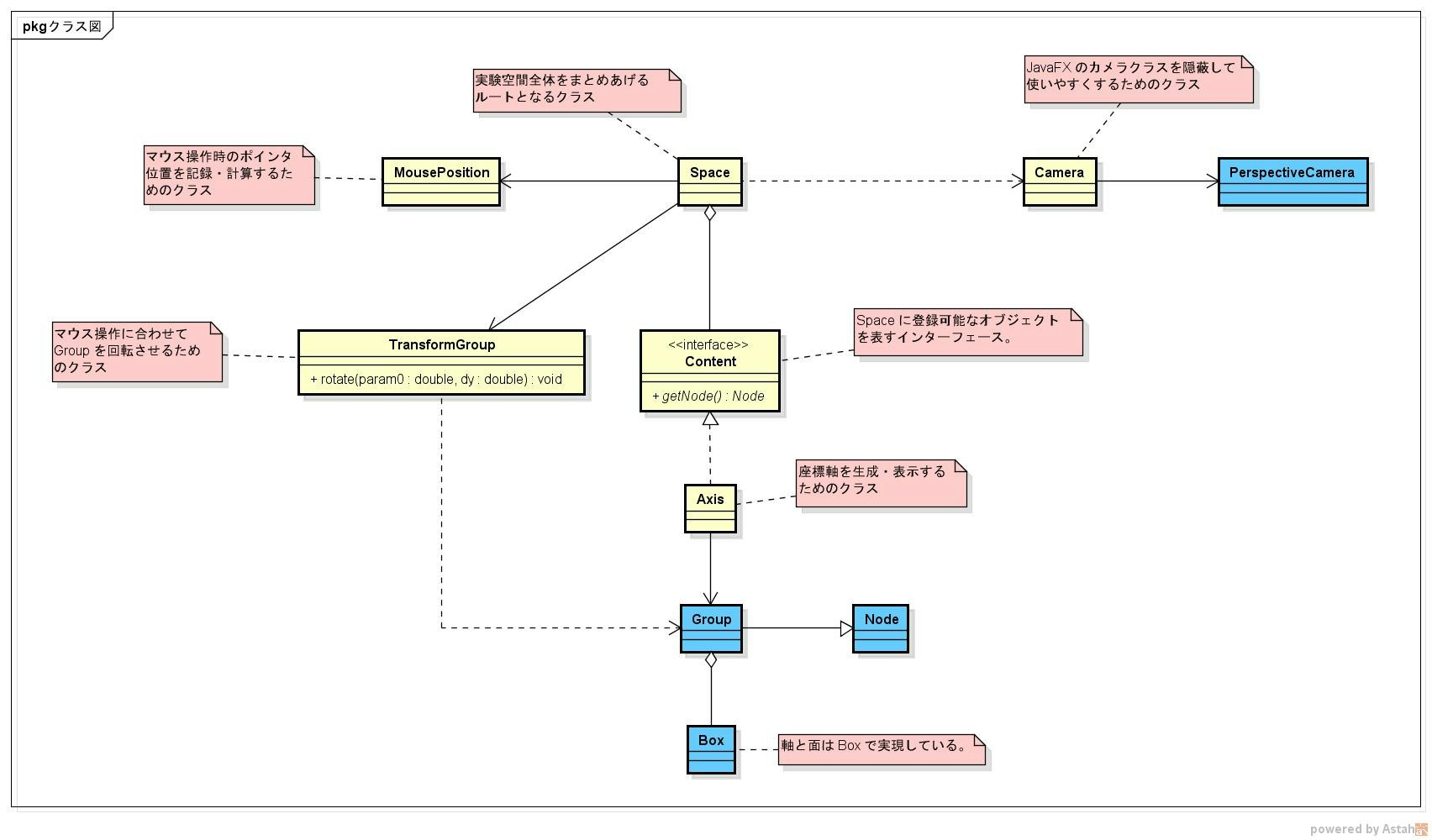
一応クラス図はこちら。
青色は、 JavaFX のライブラリが提供しているクラス。

#運動の第１法則
だいたい準備は整ったので、まずは運動の第１法則を実装してみる。

運動の第１法則とは、別名「慣性の法則」とも呼ばれるもので、「ニュートンの運動の３法則」の１つ目にあたる。

力が加えられていない物体は、静止しているものは静止し続け、運動している物体は同じ速度で運動をし続けるという法則。
この性質のことを「慣性」と呼ぶ。

法則を実装というと難しそうだけど、要は速度０の物体はその場にいつづけ、速度 $\vec{v}$ で運動する物体は、その速度を維持したまま移動し続けるようにすればいい。

##モデル
運動する単純な物体として「ボール」を考える。
また、物理法則の具象クラスとして「運動の法則」を実装する。

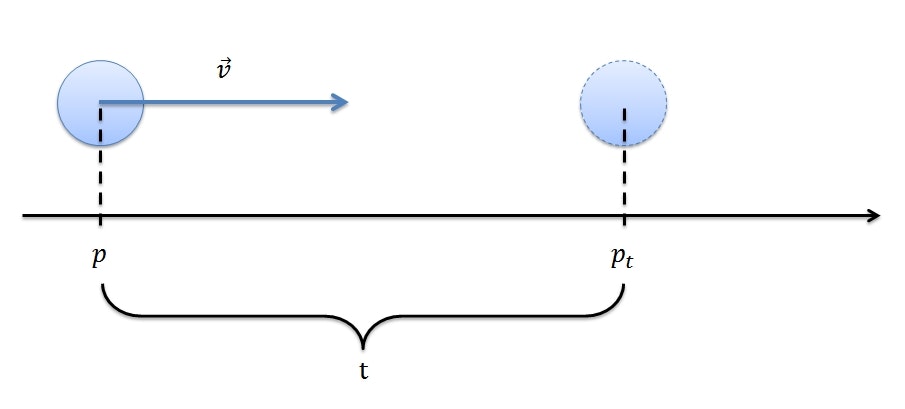
##等速直線運動している物体の位置を計算する
「ボール」にはどんな属性が必要だろうか？

とりあえず、位置を特定する必要があるので「位置」属性は必要そう。
さらに、「ボール」は移動しているので、速さと移動の向き、すなわち「速度」が必要そう。

「位置」と「速度」だけで問題ないか？
それを考えるため、同じ方向に一定の速さで運動（等速直線運動）している物体の位置の求め方を考える。

難しい言い方をすると、「最初、位置 $p (p_x, p_y, p_z)$ に存在する物体が、速度 $\vec{v} (v_x,\ v_y,\ v_z)$ で運動している場合、 $t$ 秒後の位置 $p_t$ を求める」。

簡単な言い方にすると、「Aさんは家から学校に向かって毎秒０．５メートルの速さで歩いています。最初家から１０メートルの位置にいた A さんは、１２０秒後には家から何メートルの位置にいるか」。

中学校くらいのときに習ったはずの $\frac{き}{は|じ}$ （木の下の禿げたじじぃ）を使えば簡単に求めることができる。
つまり、距離（き）は「速さ（は）×時間（じ）」で求められるということなので、 $p_t$ は次の計算で求めることができる。

\begin{eqnarray}
p_t & = & p + t \cdot \vec{v} \\
    & = & (p_x,\ p_y,\ p_z) + t \cdot (v_x,\ v_y,\ v_z) \\
    & = & (p_x,\ p_y,\ p_z) + (tv_x,\ tv_y,\ tv_z) \\
    & = & (p_x + tv_x,\ p_y + tv_y,\ p_z + tv_z)
\end{eqnarray}

時間 $t$ は Time クラスから渡されるので、この式を計算するのにあと必要なのは「速度（$\vec{v}$）」と「位置（$p$）」の２つになる。
つまり、「ボール」が現時点で持つべき属性は「速度」と「位置」だけで問題ないということになる。

##ボールを実装する

Ball.java

package gl8080.physics.domain.physical;

import java.util.Objects;

import gl8080.physics.domain.Physical;
import gl8080.physics.domain.primitive.Point;
import gl8080.physics.domain.primitive.Velocity;

public class Ball implements Physical {
    
    private Point location;
    private Velocity velocity;
    
    public Ball(Point location, Velocity velocity) {
        Objects.requireNonNull(location);
        Objects.requireNonNull(velocity);
        this.location = location;
        this.velocity = velocity;
    }
}

Point.java

package gl8080.physics.domain.primitive;

public class Point {
    public static final Point ORIGIN = new Point(0, 0, 0);
    
    public final double x;
    public final double y;
    public final double z;
    
    public Point(double x, double y, double z) {
        this.x = x;
        this.y = y;
        this.z = z;
    }
}

Velocity.java

package gl8080.physics.domain.primitive;

public class Velocity {
    public static final Velocity ZERO = new Velocity(0, 0, 0);
    
    public final double x;
    public final double y;
    public final double z;
    
    public Velocity(double x, double y, double z) {
        this.x = x;
        this.y = y;
        this.z = z;
    }
}

ついでに、「位置」と「速度」もクラスとして定義しておく。
２つのクラスはインスタンスの使い回しが想定されるので、イミュータブルにしておく（DDD の値オブジェクト的な）。

##Physical インターフェースにメソッドを追加する
計算には先ほど記述した通り、「物体」の「位置」と「速度」が必要になる。また、計算後の「位置」を再格納するためのメソッドも必要になる。

ということで、まずは Physical インターフェースを修正してこれらの値の入出力ができるようにする。

Physical.java

package gl8080.physics.domain;

import gl8080.physics.domain.primitive.Point;
import gl8080.physics.domain.primitive.Velocity;

public interface Physical {

    Velocity getVelocity();

    Point getLocation();

    void setLocation(Point location);
}

##「ボール」クラスを修正する
次に、「ボール」クラスを修正する。

Ball.java

package gl8080.physics.domain.physical;

import java.util.Objects;

import gl8080.physics.domain.Physical;
import gl8080.physics.domain.primitive.Point;
import gl8080.physics.domain.primitive.Velocity;

public class Ball implements Physical {
    
    private Point location;
    private Velocity velocity = Velocity.ZERO;

    public Ball(Point location, Velocity velocity) {
        Objects.requireNonNull(location);
        Objects.requireNonNull(velocity);
        this.location = location;
        this.velocity = velocity;
    }

    @Override
    public Point getLocation() {
        return this.location;
    }
    
    @Override
    public void setLocation(Point location) {
        Objects.requireNonNull(location);
        this.location = location;
    }

    @Override
    public Velocity getVelocity() {
        return this.velocity;
    }
}

##「運動の法則」を実装する

LawOfMotion.java

package gl8080.physics.domain.law;

import gl8080.physics.domain.Physical;
import gl8080.physics.domain.PhysicalLaw;
import gl8080.physics.domain.primitive.Point;
import gl8080.physics.domain.primitive.Velocity;

public class LawOfMotion implements PhysicalLaw {
    
    @Override
    public void apply(Physical physical, double t) {
        Velocity v = physical.getVelocity();
        Point p = physical.getLocation();
        
        Point pt = new Point(p.x + t*v.x, p.y + t*v.y, p.z + t*v.z);
        
        physical.setLocation(pt);
    }
}

new Point(p.x + t*v.x, p.y + t*v.y, p.z + t*v.z) ← この部分の引数が、前述の計算式と同じになっている。

ただ、このままだとオブジェクト指向っぽくなくて気持ち悪いので、若干リファクタリングして Point クラスに add() メソッドを追加する。

LawOfMotion.java

    ...

    @Override
    public void apply(Physical physical, double t) {
        Velocity v = physical.getVelocity();
        Point p = physical.getLocation();
        
        Point pt = p.add(t*v.x, t*v.y, t*v.z);
        
        physical.setLocation(pt);
    }

    ...

##ボールのビュークラスを作成する
Ball はドメインクラスで、それ自体は画面にボールを表示するための仕組みを持っていない。
なので、ボールを画面に表示するためのビュークラスを作る。

###モデル

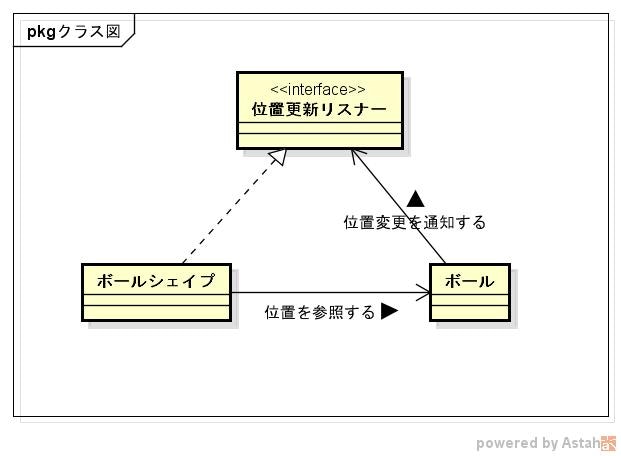
「ボールシェイプ」クラスは「ボール」クラスの位置情報を参照することで、その位置に球体を表示する。
また、「ボール」クラスの位置が「運動の法則」によって変更された場合、そのことを通知するためにリスナーを用意する。

###実装

BallShape.java

package gl8080.physics.view.shape;

import java.util.function.Consumer;

import gl8080.physics.domain.physical.Ball;
import gl8080.physics.domain.primitive.Point;
import gl8080.physics.view.Content;
import javafx.scene.Node;
import javafx.scene.shape.Sphere;
import javafx.scene.transform.Translate;

public class BallShape implements Content, Consumer<Point> {
    
    private Sphere sphere;
    private Translate translate = new Translate();

    public BallShape(Ball ball, double radius) {
        this.sphere = new Sphere(radius);
        this.sphere.getTransforms().add(this.translate);
        ball.addLocationListener(this);
        this.translate(ball.getLocation());
    }
    
    public void translate(Point point) {
        this.translate.setX(point.x);
        this.translate.setY(point.y);
        this.translate.setZ(point.z);
    }
    
    @Override
    public Node getNode() {
        return this.sphere;
    }

    @Override
    public void accept(Point location) { // ★このメソッドで位置更新の通知を受け取る
        this.translate(location);
    }
}

「ボール」の方も、リスナーに位置変更を通知できるように修正する。

Ball.java

package gl8080.physics.domain.physical;

import java.util.HashSet;
import java.util.Objects;
import java.util.Set;
import java.util.function.Consumer;

import gl8080.physics.domain.Physical;
import gl8080.physics.domain.primitive.Point;
import gl8080.physics.domain.primitive.Velocity;

public class Ball implements Physical {
    
    ...
    private Set<Consumer<Point>> locationListeners = new HashSet<>();
    
    ...
    
    @Override
    public void setLocation(Point location) {
        Objects.requireNonNull(location);
        this.location = location;
        this.locationListeners.forEach(listener -> listener.accept(location)); // ★ここで変更を通知
    }

    ...

    public void addLocationListener(Consumer<Point> listener) {
        Objects.requireNonNull(listener);
        this.locationListeners.add(listener);
    }
}

##「世界」に「ボール」と「運動の法則」を追加して動かす
役者は揃ったので、それぞれ「世界」に登録して動かしてみる。

Main.java

package gl8080.physics;

import java.util.concurrent.ExecutorService;
import java.util.concurrent.Executors;

import gl8080.physics.domain.Time;
import gl8080.physics.domain.World;
import gl8080.physics.domain.law.LawOfMotion;
import gl8080.physics.domain.physical.Ball;
import gl8080.physics.domain.primitive.Point;
import gl8080.physics.domain.primitive.Velocity;
import gl8080.physics.view.Axis;
import gl8080.physics.view.Camera;
import gl8080.physics.view.Space;
import gl8080.physics.view.shape.BallShape;
import javafx.application.Application;
import javafx.scene.Group;
import javafx.scene.Parent;
import javafx.scene.Scene;
import javafx.stage.Stage;

public class Main extends Application {
    
    public static void main(String[] args) {
        launch(args);
    }
    
    private ExecutorService service = Executors.newSingleThreadExecutor();
    private Time time;
    
    @Override
    public void start(Stage primaryStage) throws Exception {
        primaryStage.setResizable(false);
        Scene root = new Scene(createContent());
        primaryStage.setScene(root);
        primaryStage.show();
        
        primaryStage.setOnCloseRequest(e -> {
            this.time.stop();
            this.service.shutdown();
        });
    }

    public Parent createContent() throws Exception {
        // ボールを作る
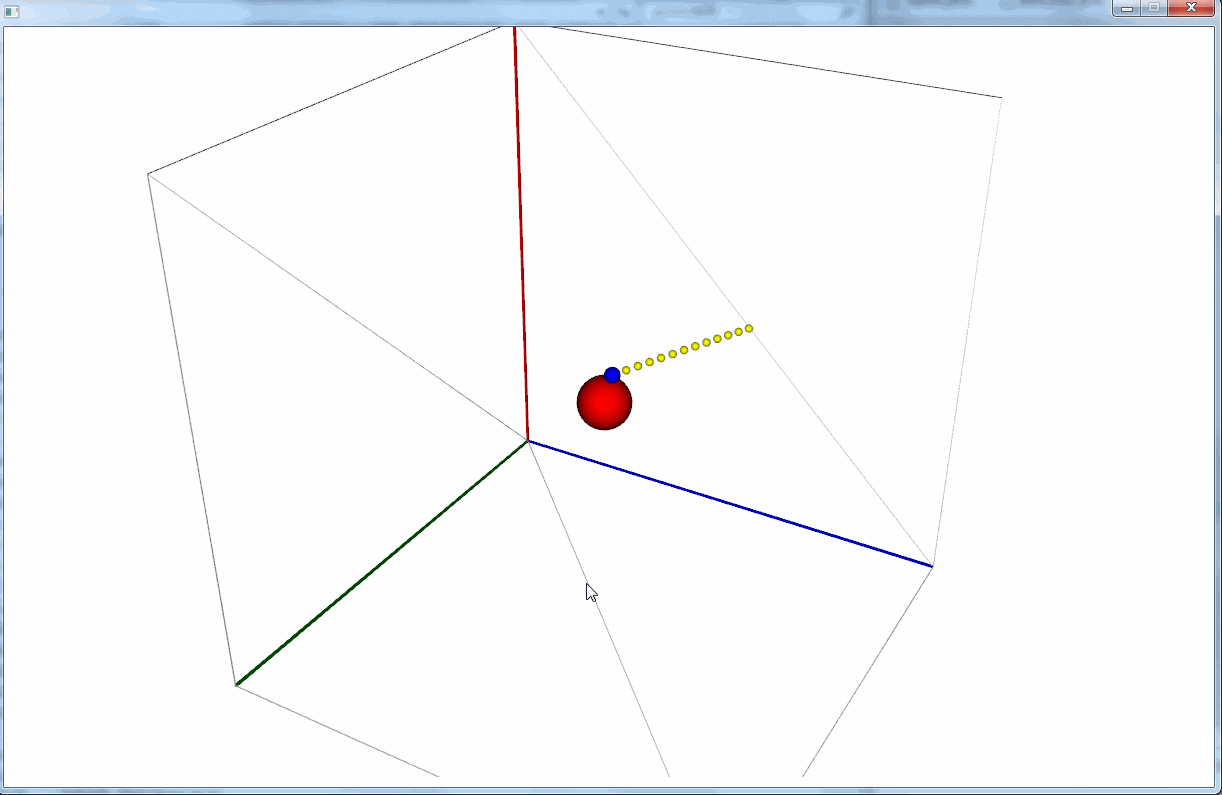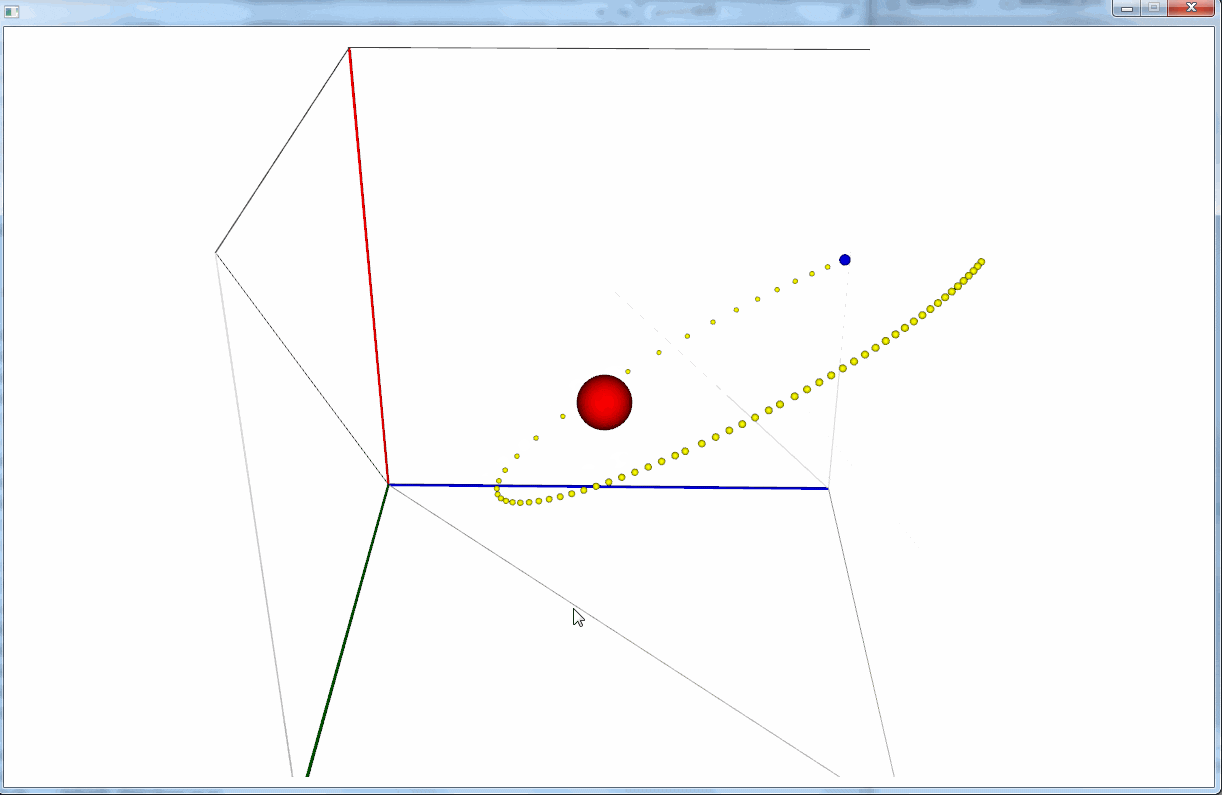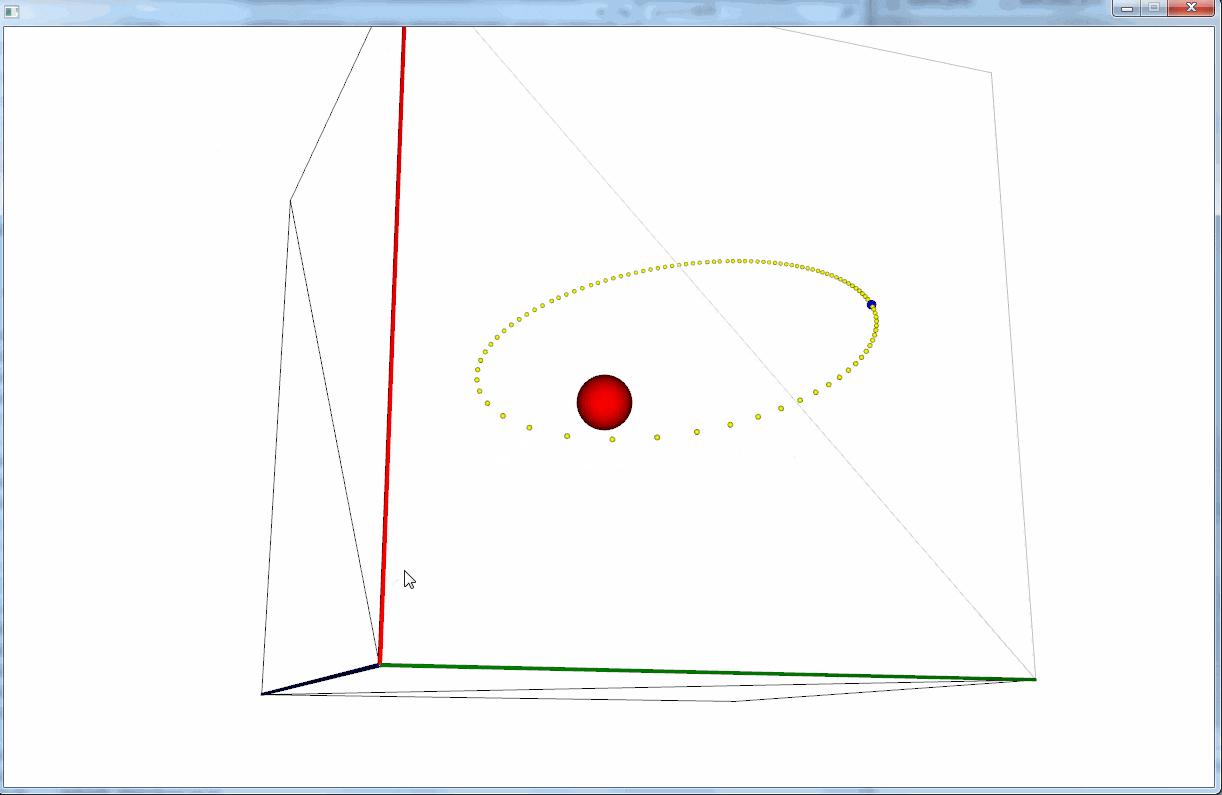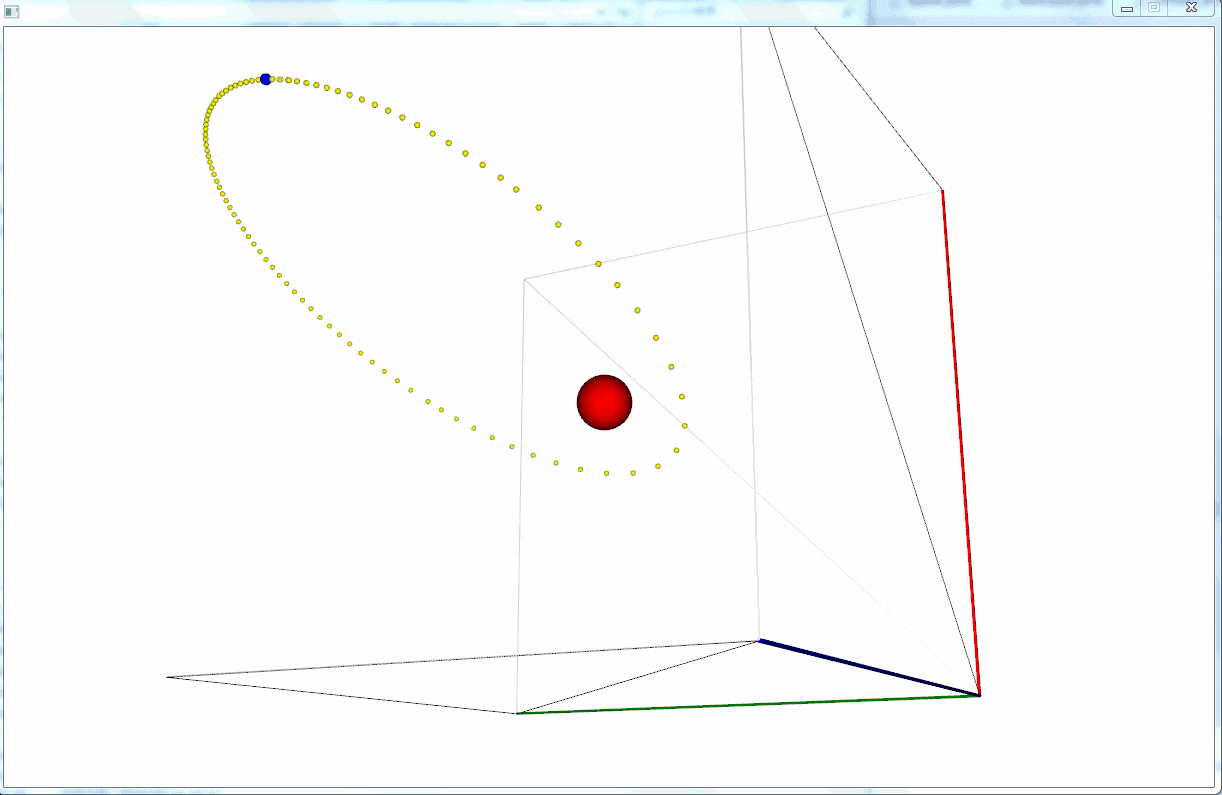
        Point location = new Point(80, 10, 10); // 初期位置
        Velocity velocity = new Velocity(-5.0, 3.0, 6.0); // 速度
        Ball ball = new Ball(location, velocity);
        
        // 実験空間の用意
        final double size = 100;
        Space space = new Space(size, new Camera());
        space.add(new Axis(size));
        
        // ボールのシェイプを作り、空間に追加する
        BallShape ballShape = new BallShape(ball, 1.0);
        space.add(ballShape);
        
        // 世界を作り、ボールと物理法則を追加する
        World world = new World();
        world.addPhysical(ball);
        world.addPhysicalLaws(new LawOfMotion());
        
        // 時の流れをスタートさせる
        this.time = new Time(world);
        
        this.service.execute(() -> {
            this.time.start();
        });
        
        return new Group(space.getSubScene());
    }
}

いい感じで等速直線運動をしている。

#運動の第２法則
第１法則は実装したので、次は第２法則。

第２法則では、物体に働く力と加速度の関係を式で表現している。

\vec{F} = m\vec{a}

$\vec{F}$ は物体に働く力。 $m$ は物体の質量。 $\vec{a}$ は物体の加速度を意味している。

この式のことを 運動方程式 と呼ぶ。

要は、物体に力が働いている場合、その物体は力の作用している向きに加速することを意味している（力が働いていない場合は静止するか等速直線運動する）。

この式を使うと地上の物体はもちろん、惑星の運動まで計算で求めることができるので、古典力学において非常に重要な方程式として扱われている。

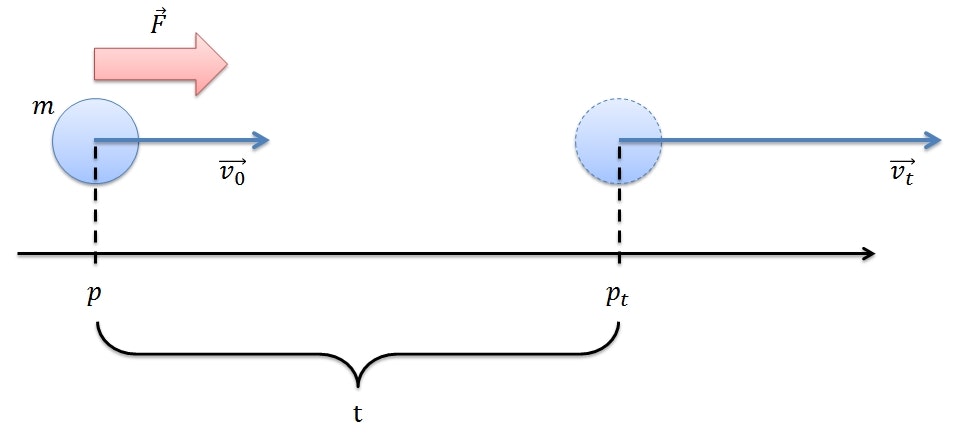
##力が加えられている物体の位置と速度を計算する
初期位置 $p$ 、初速度 $\vec{v_0}$ で運動している質量 $m$ の物体に、 $\vec{F}$ の力を $t$ 秒間加えたときの最終的な位置 $p_t$ と速度 $\vec{v_t}$ を求める。

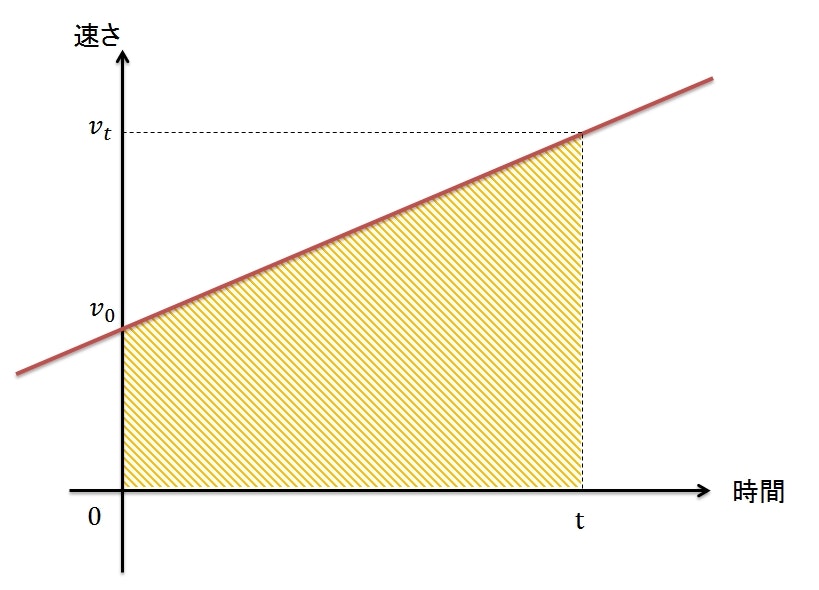
これを考えるときは、横軸を時間、縦軸を速さにしたグラフを描くとイメージしやすい。

単純な１次関数のグラフなので、$t$ 秒後の速さ $v_t$ は以下の式で求められる。

v_t = v_0 + at

ここで、 $a$ はグラフの傾き（速さの時間変化）、すなわち加速度を表している。

加速度は先ほどの運動方程式から $F = ma$ → $a = \frac{F}{m}$ とできるので、こいつを上の式に代入する。

\begin{eqnarray}
v_t & = & v_0 + at \\
    & = & v_0 + \frac{F}{m}t \\
\end{eqnarray}

これで、初速・力・質量の３つさえ分かれば、 $t$ 秒後の物体の速さを計算できることが分かった。

次は移動距離 $x$ を求める。

距離は、速さ×時間で求められる。先ほどの図を見ると、速さ×時間はちょうどオレンジの斜線で着色された領域の面積を表している。
ということで、このオレンジ部分の面積を求めれば、 $t$ 秒後の移動距離 $x$ が求められることになる。

台形の面積は、（上底＋下底）×高さ÷２で求められるので、 $t$ 秒後の移動距離 $x$ は以下の式で求められる。

\begin{eqnarray}
x & = & \frac{t}{2}(v_0 + v_t)
\end{eqnarray}

$v_t$ は先ほど計算しているので、移動距離も、初速・力・質量の３つが分かれば計算できることが分かる。

##モデル
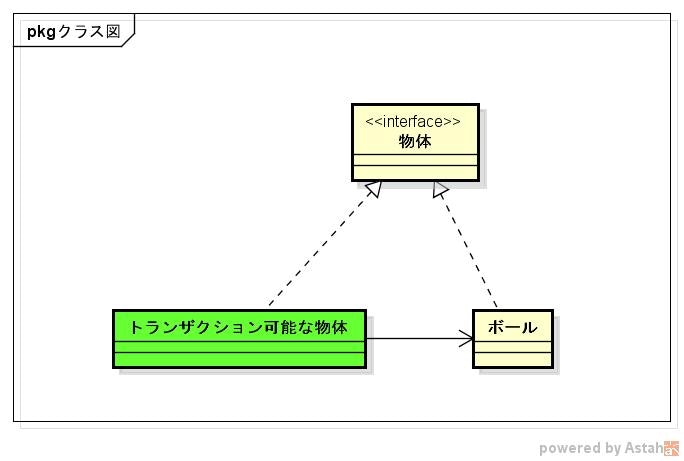
新しく力という重要な概念が登場したので、力を扱えるようにモデルを更新する。

緑色のクラスが、追加したクラス（いい感じの名前が思いつかなかった。。。）。

以下のように使うイメージ。

物体には何らかの「力」が作用している。重力（万有引力）、摩擦力、垂直抗力、遠心力などなど。
しかし、結局のところそれらの合力が分かれば位置や速度の計算はできる。なので、そのへんの諸々は「作用する力」で抽象化して、「運動の法則」は受け取った最終的な力だけを使って計算を行う。

##実装する
「作用する力」「力」「質量」をそれぞれ実装する。

ActingForce.java

package gl8080.physics.domain;

import gl8080.physics.domain.force.Force;

public interface ActingForce {
    
    Force getForce(Physical target);
}

Force.java

package gl8080.physics.domain.primitive;

public class Force {
    
    public final double x;
    public final double y;
    public final double z;
    
    public Force(double x, double y, double z) {
        this.x = x;
        this.y = y;
        this.z = z;
    }
}

Mass.java

package gl8080.physics.domain.primitive;

public class Mass {
    public static final Mass ZERO = new Mass(0.0);
    
    public final double quantity;

    public Mass(double quantity) {
        this.quantity = quantity;
    }
}

さらに、「物質」に必要なメソッドを追加する。

Physical.java

package gl8080.physics.domain;

import gl8080.physics.domain.primitive.Mass;
import gl8080.physics.domain.primitive.Point;
import gl8080.physics.domain.primitive.Velocity;

public interface Physical {
    Velocity getVelocity();
    Point getLocation();
    Mass getMass(); // ★追加
    void setLocation(Point location);
    void setVelocity(Velocity velocity); // ★追加
}

実装は省略するが、「ボール」クラスもこの変更に合わせて修正しておく。

最後に、「運動の法則」を「力」に対応させる。

LawOfMotion.java

package gl8080.physics.domain.law;

import java.util.Objects;

import gl8080.physics.domain.ActingForce;
import gl8080.physics.domain.Physical;
import gl8080.physics.domain.PhysicalLaw;
import gl8080.physics.domain.primitive.Force;
import gl8080.physics.domain.primitive.Mass;
import gl8080.physics.domain.primitive.Point;
import gl8080.physics.domain.primitive.Velocity;

public class LawOfMotion implements PhysicalLaw {
    
    private final ActingForce actingForce;

    public LawOfMotion(ActingForce actingForce) {
        Objects.requireNonNull(actingForce);
        this.actingForce = actingForce;
    }

    @Override
    public void apply(Physical physical, double t) {
        Force f = this.actingForce.getForce(physical); // ★物体に働く力を取得して
        Velocity v0 = physical.getVelocity();
        Mass m = physical.getMass();
        
        Velocity vt = this.calcVelocity(v0, f, m, t); // ★速度と
        
        Point p0 = physical.getLocation();
        Point pt = this.calcLocation(p0, v0, vt, t); // ★位置を計算して
        
        physical.setVelocity(vt); // ★物体の状態を更新
        physical.setLocation(pt);
    }
    
    private Velocity calcVelocity(Velocity v0, Force f, Mass m, double t) {
        double vtx = v0.x + f.x * t / m.quantity;
        double vty = v0.y + f.y * t / m.quantity;
        double vtz = v0.z + f.z * t / m.quantity;
        
        return new Velocity(vtx, vty, vtz);
    }
    
    private Point calcLocation(Point p0, Velocity v0, Velocity vt, double t) {
        double xt = p0.x + t * (v0.x + vt.x) / 2.0;
        double yt = p0.y + t * (v0.y + vt.y) / 2.0;
        double zt = p0.z + t * (v0.z + vt.z) / 2.0;
        
        return new Point(xt, yt, zt);
    }
}

ActingForce から物体に働く力を取得し、その力を元に位置と速度を計算している。

##重力を追加する
身近な力として、地球の重力を追加してみる。

EarthGravity.java

package gl8080.physics.domain.force;

import gl8080.physics.domain.ActingForce;
import gl8080.physics.domain.Physical;
import gl8080.physics.domain.primitive.Force;
import gl8080.physics.domain.primitive.Mass;

public class EarthGravity implements ActingForce {

    @Override
    public Force getForce(Physical target) {
        Mass mass = target.getMass();
        return new Force(0.0, mass.quantity * -9.8, 0.0);
    }
}

運動方程式 $\vec{F} = m\vec{a}$ から、物体にかかる力は、物体の質量×加速度で求められる。
重力加速度は $9.8 m/s^2$ で、かつ $y$ 軸下向きに働く力なので、 $-9.8m$ で重力によって加えられる力が求められる。

##動かす
役者は揃ったので、ここまでのクラスを組み合わせて実際に動かしてみる。

Main.java

package gl8080.physics;

// ...

public class Main extends Application {
    
    // ...

    public Parent createContent() throws Exception {
        // ボールを作る
        Mass mass = new Mass(10.0); // ★質量
        Point location = new Point(0.0, 0.0, 100.0); // 初期位置
        Velocity velocity = new Velocity(12.5, 40.0, -12.5); // 速度
        Ball ball = new Ball(mass);
        ball.setLocation(location);
        ball.setVelocity(velocity);
        
        // 実験空間の用意
        final double size = 100;
        Space space = new Space(size, new Camera());
        space.add(new Axis(size));
        
        // ボールのシェイプを作り、空間に追加する
        BallShape ballShape = new BallShape(ball, 1.0);
        space.add(ballShape);
        
        // 世界を作り、ボールと物理法則を追加する
        ActingForce actingForce = new EarthGravity(); // ★重力を追加
        PhysicalLaw law = new LawOfMotion(actingForce);
        
        World world = new World();
        world.addPhysical(ball);
        world.addPhysicalLaws(law);
        
        // 時の流れをスタートさせる
        // ...
    }
}

ちゃんと放物線運動している。
動きがゆっくりに見えるが、軸の一辺は $100m$ もあるので、遠くから眺めている図だと考えれば納得できると思う（実際 $140m$ くらいの距離を数秒で移動しているので、結構速い）。

#円運動
「力」を実装できたので、理屈上簡単に円運動を実現できるはず（運動の第３法則は当たり判定とかが絡んできてややこしいので飛ばす）。

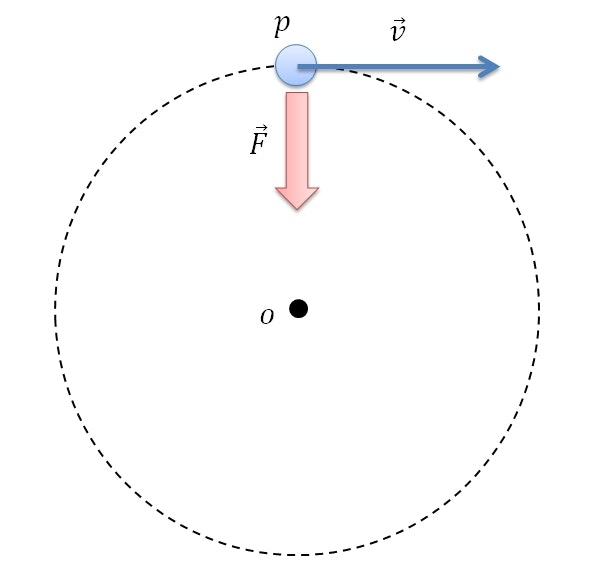
等速直線運動している物体に対して常に垂直に働く一定の大きさの力を加わえ続けると、その物体は等速円運動を行うようになる。

$\vec{F}$ が、中心に向かって引っ張る力――向心力を表している。

##向心力を求める
物体が等速円運動している場合、質量・速さ・向心力には次の関係が成り立つ。

|\vec{F}| = m\frac{|\vec{v}|^2}{r}

ここで、 $|\vec{F}|$ は向心力の大きさ、 $m$ は質量、 $|\vec{v}|$ は物体の速さ、 $r$ は円の半径を表す。

向心力 $\vec{F}$ は次の式で求められる。

\begin{eqnarray}
\vec{F} & = & |\vec{F}|\frac{\vec{po}}{|\vec{po}|}
\end{eqnarray}

$\vec{po}$ は物体から中心へ向かうベクトルで、そのベクトルの大きさ $|\vec{po}|$ で割ることで、中心へ向かう長さ１のベクトルを求めている。
そして、そこに向心力の大きさである $|\vec{F}|$ を掛けることで、中心へ向かう大きさ $|\vec{F}|$ のベクトル、すなわち $\vec{F}$ を求めている。
（長さが１のベクトルのことを単位ベクトルと呼び、単位ベクトルを求めることを正規化（normalize）と呼ぶ）

ちなみに、 $\vec{po}$ と $|\vec{po}|$ は次の式で求められる。

\begin{eqnarray}
\vec{po} & = & (o_x - p_x, o_y - p_y, o_z - p_z)
\end{eqnarray}

\begin{eqnarray}
|\vec{po}| & = & \sqrt{(o_x - p_x)^2 + (o_y - p_y)^2 + (o_z - p_z)^2}
\end{eqnarray}

##向心力を実装する
上述の式を使って、向心力を実装してみる。

CentripetalForce.java

package gl8080.physics.domain.force;

import java.util.Objects;

import gl8080.physics.domain.ActingForce;
import gl8080.physics.domain.Physical;
import gl8080.physics.domain.primitive.Force;
import gl8080.physics.domain.primitive.Point;
import gl8080.physics.domain.primitive.Vector;
import gl8080.physics.domain.primitive.Velocity;

public class CentripetalForce implements ActingForce {
    
    private final Point center;
    
    public CentripetalForce(Point center) {
        Objects.requireNonNull(center);
        this.center = center;
    }

    @Override
    public Force getForce(Physical target) {
        
        Point p = target.getLocation();

        // 力の大きさを求める
        double rx = this.center.x - p.x;
        double ry = this.center.y - p.y;
        double rz = this.center.z - p.z;
        double r = Math.sqrt(rx*rx + ry*ry + rz*rz);
        
        Velocity v = target.getVelocity();
        double vv = v.x*v.x + v.y*v.y + v.z*v.z;
        
        double m = target.getMass().quantity;
        
        double quantityOfForce = m * vv / r;
        
        // po ベクトルを求め
        Vector po = Vector.create(p, this.center);
        // 正規化し
        Vector e = po.normalize();
        // 力の大きさを掛ける
        Vector f = e.multiply(quantityOfForce);

        return new Force(f.x, f.y, f.z);
    }
}

Vector.java

package gl8080.physics.domain.primitive;

public class Vector {
    
    public final double x;
    public final double y;
    public final double z;
    
    public static Vector create(Point from, Point to) {
        return new Vector(to.x - from.x, to.y - from.y, to.z - from.z);
    }
    
    public Vector(double x, double y, double z) {
        this.x = x;
        this.y = y;
        this.z = z;
    }
    
    public Vector normalize() {
        double norm = this.getNorm();
        return new Vector(this.x/norm, this.y/norm, this.z/norm);
    }
    
    public Vector multiply(double d) {
        return new Vector(this.x * d, this.y * d, this.z * d);
    }
    
    public double getNorm() {
        return Math.sqrt(this.x*this.x + this.y*this.y + this.z*this.z);
    }
}

ベクトルの演算は Vector クラスにまとめた。

##動かしてみる
試しに動かしてみる。

Main.java

package gl8080.physics;

// ...

public class Main extends Application {
    
    // ...

    public Parent createContent() throws Exception {
        // ボールを作る
        Mass mass = new Mass(10.0);
        Point location = new Point(50.0, 80.0, 25.0); // 初期位置
        Velocity velocity = new Velocity(20.0, 0.0, 0.0); // 速度
        Ball ball = new Ball(mass);
        ball.setLocation(location);
        ball.setVelocity(velocity);
        
        // 実験空間の用意
        // ...
        
        // ボールのシェイプを作り、空間に追加する
        // ...
        
        // ★物理法則を作り、力に向心力を設定
        Point center = new Point(50.0, 50.0, 50.0);
        ActingForce actingForce = new CentripetalForce(center);
        PhysicalLaw law = new LawOfMotion(actingForce);

        // 世界を作り、ボールと物理法則を追加する
        World world = new World();
        world.addPhysical(ball);
        world.addPhysicalLaws(law);
        
        // 時の流れをスタートさせる
        // ...
    }
}

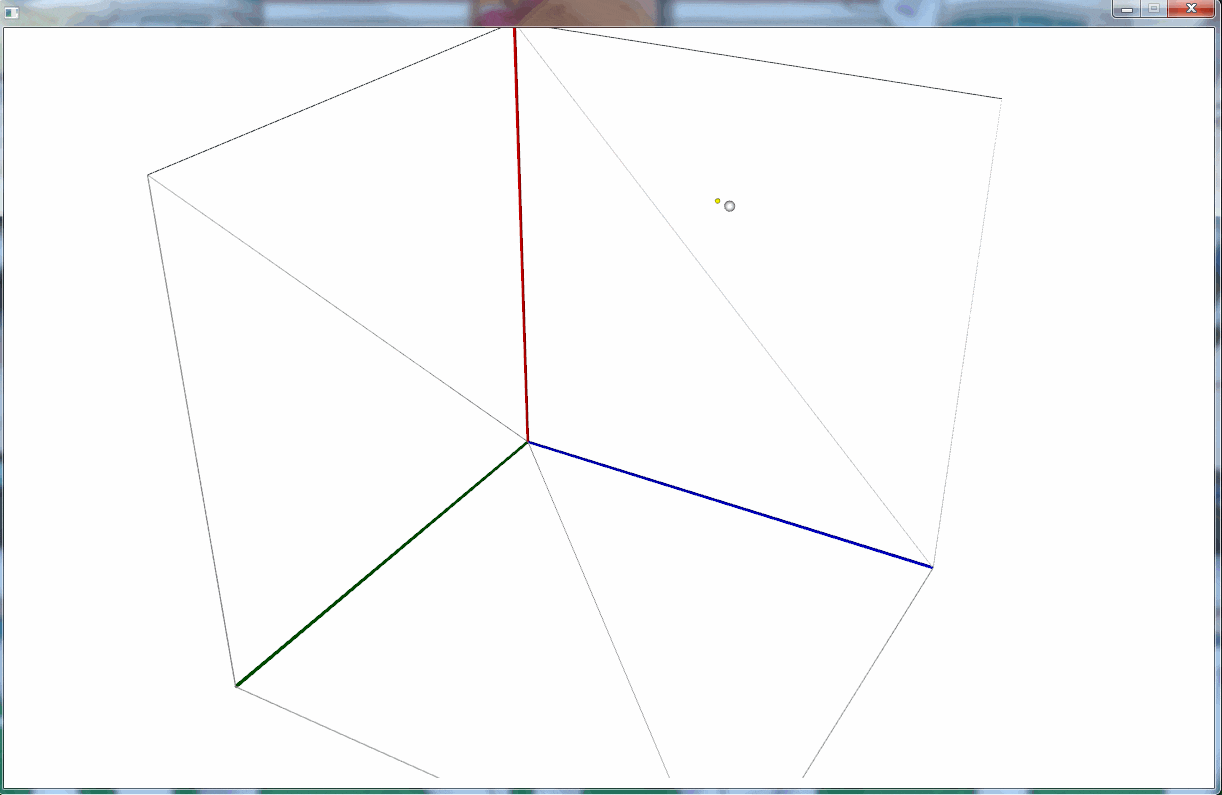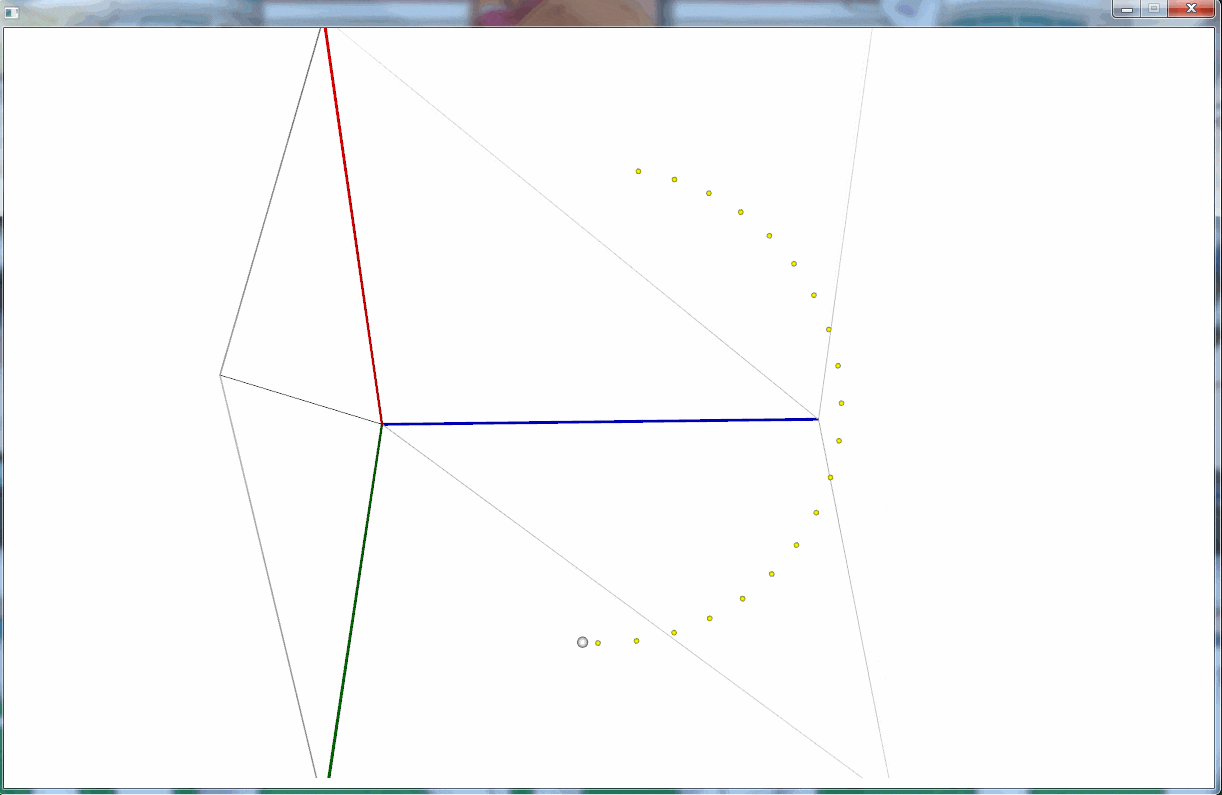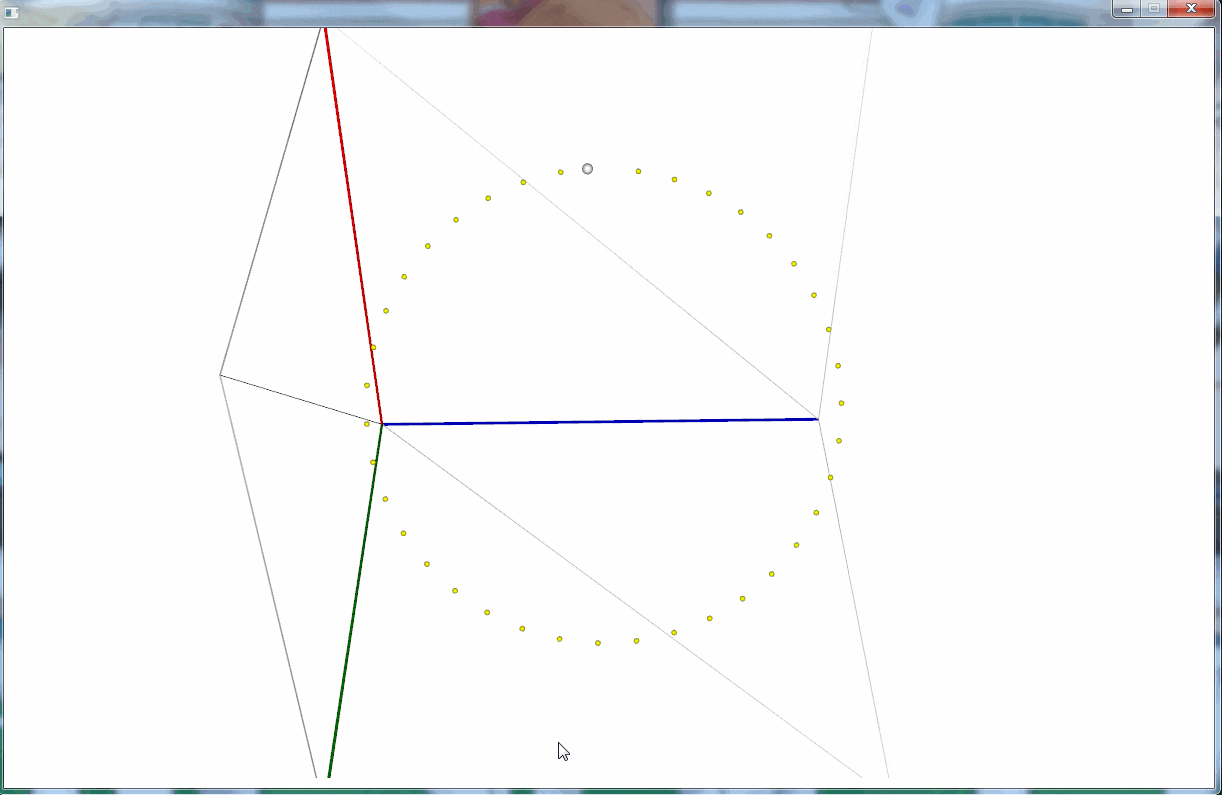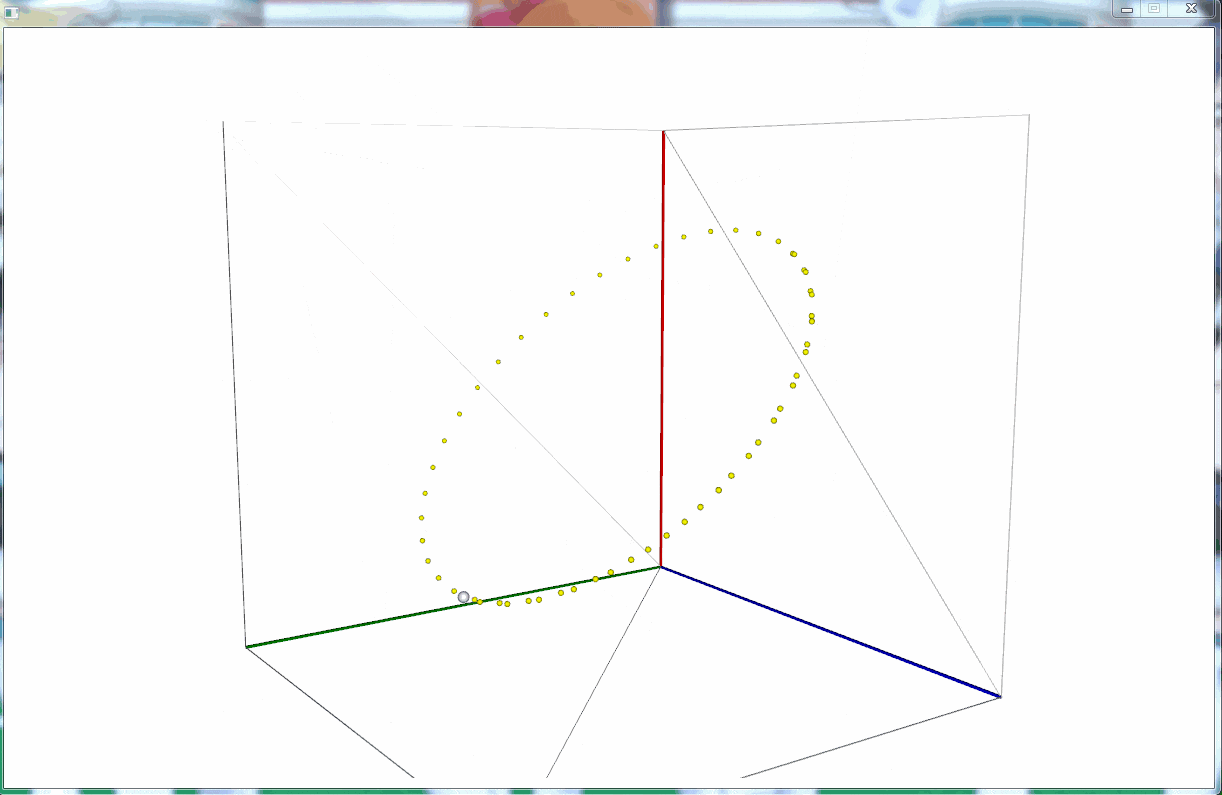
円運動しているように見えなくもない。

というか、軌跡がないとわかりづらい。。。

軌跡を表示できるよう改良してみる。

##物体の軌跡を表示させる
デザインパターンのデコレータパターンを活用して、物体の軌跡を表示させる。

BallLocus.java

package gl8080.physics.view.shape;

import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Objects;

import gl8080.physics.domain.Physical;
import gl8080.physics.domain.PhysicalLaw;
import gl8080.physics.domain.primitive.Point;
import gl8080.physics.view.Content;
import javafx.application.Platform;
import javafx.scene.Group;
import javafx.scene.Node;
import javafx.scene.paint.Color;
import javafx.scene.paint.Material;
import javafx.scene.paint.PhongMaterial;
import javafx.scene.shape.Sphere;

public class BallLocus implements Content, PhysicalLaw {

    private int historySzie;
    private Color color;
    private double radius;
    private int interval;
    
    private PhysicalLaw law;
    private Group group = new Group();
    private Deque<Sphere> spheres = new ArrayDeque<>();
    private int count;

    public static BallLocusBuilder create(PhysicalLaw law) {
        return new BallLocusBuilder(law);
    }
    
    @Override
    public Node getNode() {
        return this.group;
    }

    @Override
    public void apply(Physical ball, double sec) {
        this.count++;
        
        if (this.count % this.interval == 0) {
            // ★一定間隔で軌跡を表示する
            this.drawLocus(ball);
            this.count = 0;
        } 
        
        // ★軌跡以外の処理は、ラップしている本来のクラスに委譲
        this.law.apply(ball, sec);
    }
    
    private void drawLocus(Physical ball) {
        // Main スレッド以外で UI を操作するとエラーになるので、 Platform.runLater() を使って UI スレッドで処理を実行する
        Platform.runLater(() -> {
            Sphere sphere = this.createSphere(ball);
            this.spheres.addLast(sphere);
            this.group.getChildren().add(sphere);
            
            if (this.historySzie < this.spheres.size()) {
                Sphere removed = this.spheres.removeFirst();
                this.group.getChildren().remove(removed);
            }
        });
    }
    
    private Sphere createSphere(Physical ball) {
        // ★軌跡には、少し小さい黄色い球を用いる
        Sphere sphere = new Sphere(this.radius);
        
        Point location = ball.getLocation();
        sphere.setTranslateX(location.x);
        sphere.setTranslateY(location.y);
        sphere.setTranslateZ(location.z);
        
        Material material = new PhongMaterial(this.color);
        sphere.setMaterial(material);
        
        return sphere;
    }
    
    private BallLocus() {}
    
    public static class BallLocusBuilder {
        // （ビルダーパターンで実装）
    }
}

PhysicalLaw をラップして、 Physical の位置に黄色い Sphere を置いていく実装にしている。

###別スレッドから UI を書き換える
１点注意なのが、 JavaFX では UI 用のスレッド以外から UI を書き換える処理（Group#getChildren().add() の部分）を実行すると、エラーになるという点。
UI を書き換える場合は、 UI スレッドから実行しないといけないらしい（Android も同じ制約が存在するっぽい）。

そのため、別スレッドから UI を変更するための API として、 Platform#runLater(Runnable) というメソッドが用意されている。
丁度、 Android の Handler と同じか。

###動作確認
とりあえず、これを使ってもう一度円運動の動作を確認してみる。

Main.java

package gl8080.physics;

// ...

public class Main extends Application {
    
    // ...

    public Parent createContent() throws Exception {
        // ボールを作る
        // ...
        
        // 実験空間の用意
        // ...
        
        // ボールのシェイプを作り、空間に追加する
        // ...
        
        // 物理法則を作り、力に向心力を設定
        Point center = new Point(50.0, 50.0, 50.0);
        ActingForce actingForce = new CentripetalForce(center);
        PhysicalLaw law = new LawOfMotion(actingForce);
        
        // ★軌跡の表示を追加
        BallLocus locus = BallLocus.create(law).historySize(55).radius(0.5).build();
        space.add(locus);

        // 世界を作り、ボールと物理法則を追加する
        World world = new World();
        world.addPhysical(ball);
        world.addPhysicalLaws(locus); // ★BallLocus を設定する
        
        // 時の流れをスタートさせる
        // ...
    }
}

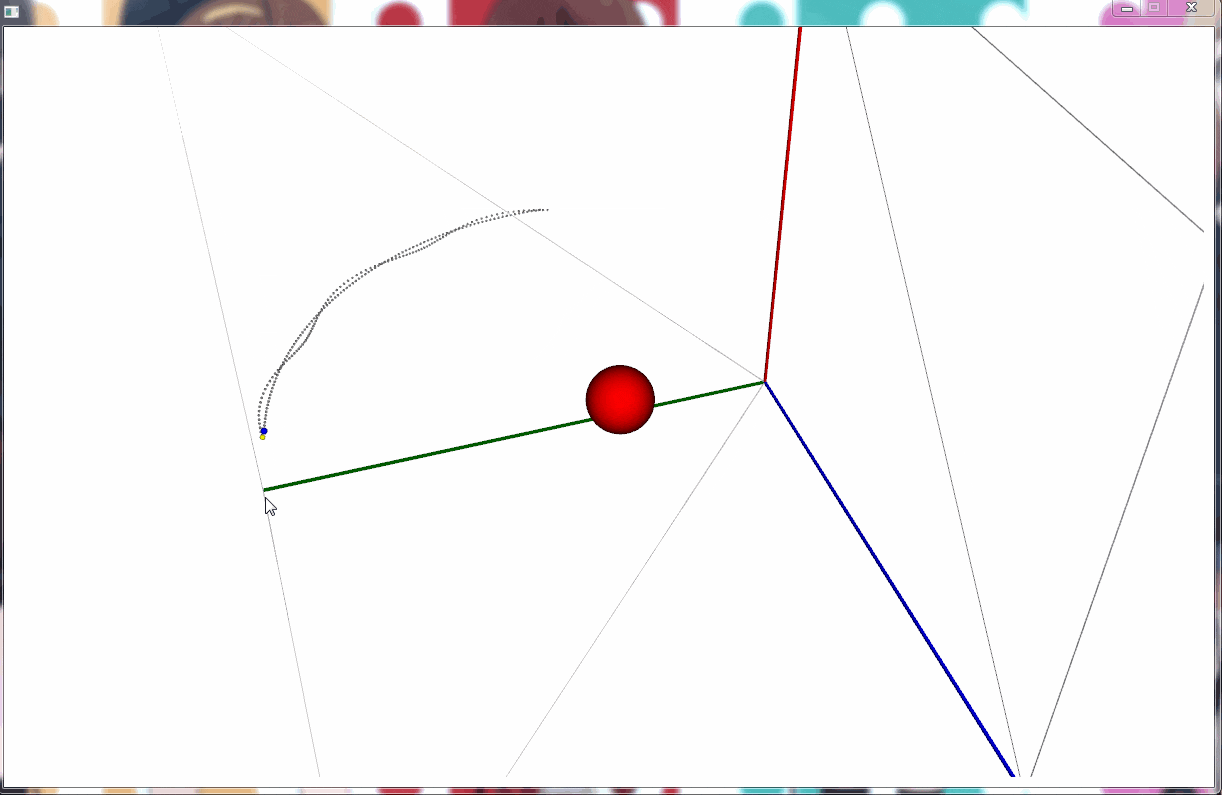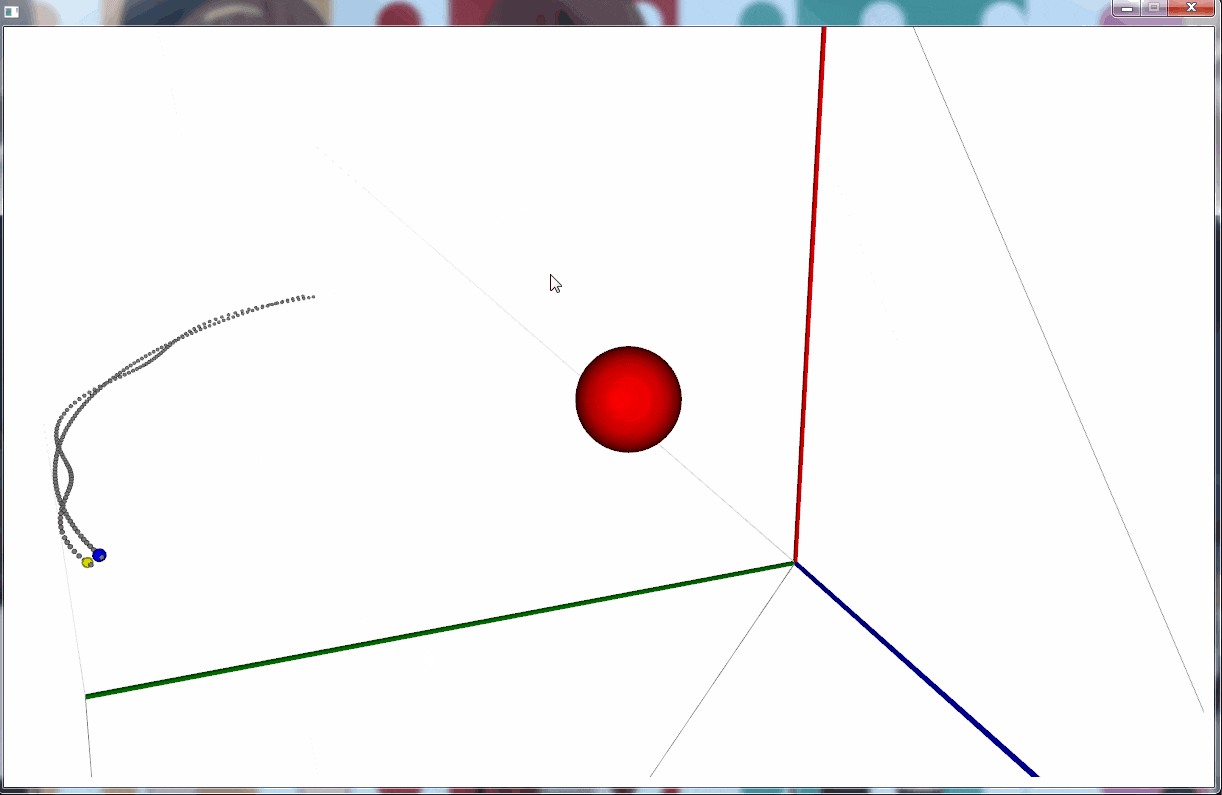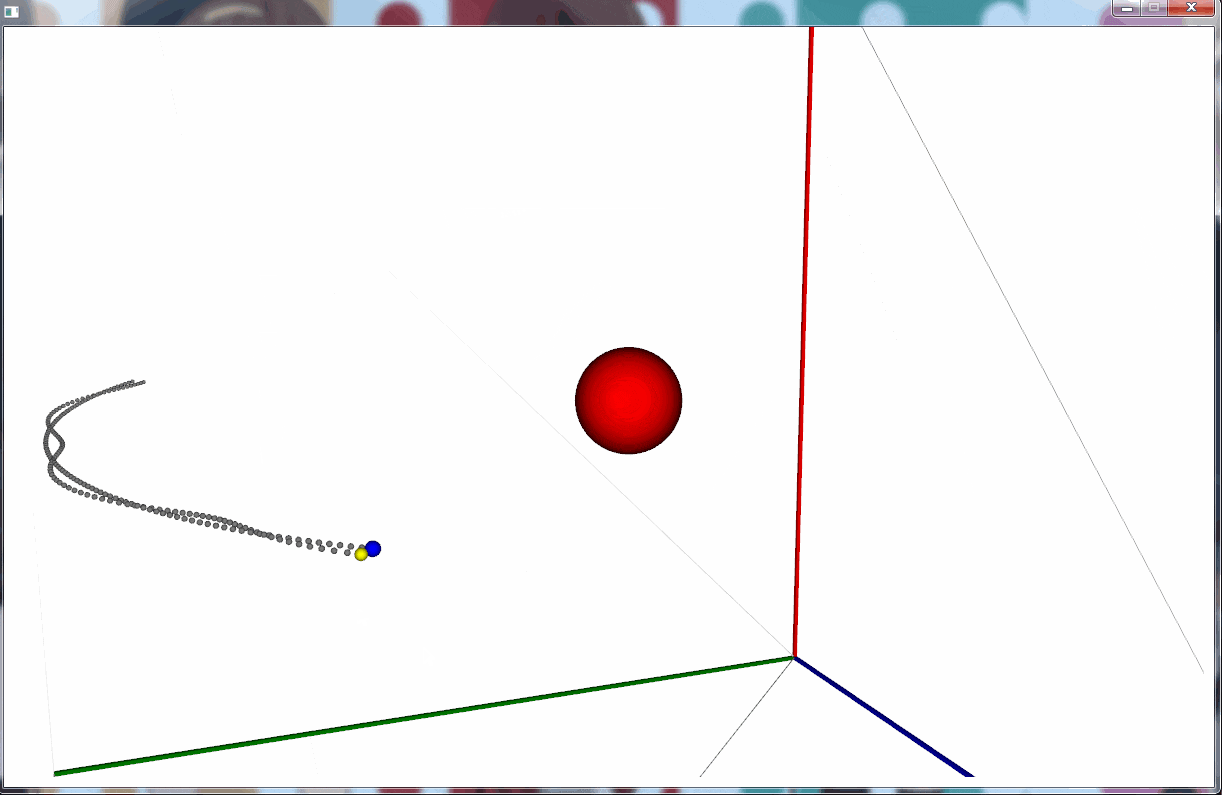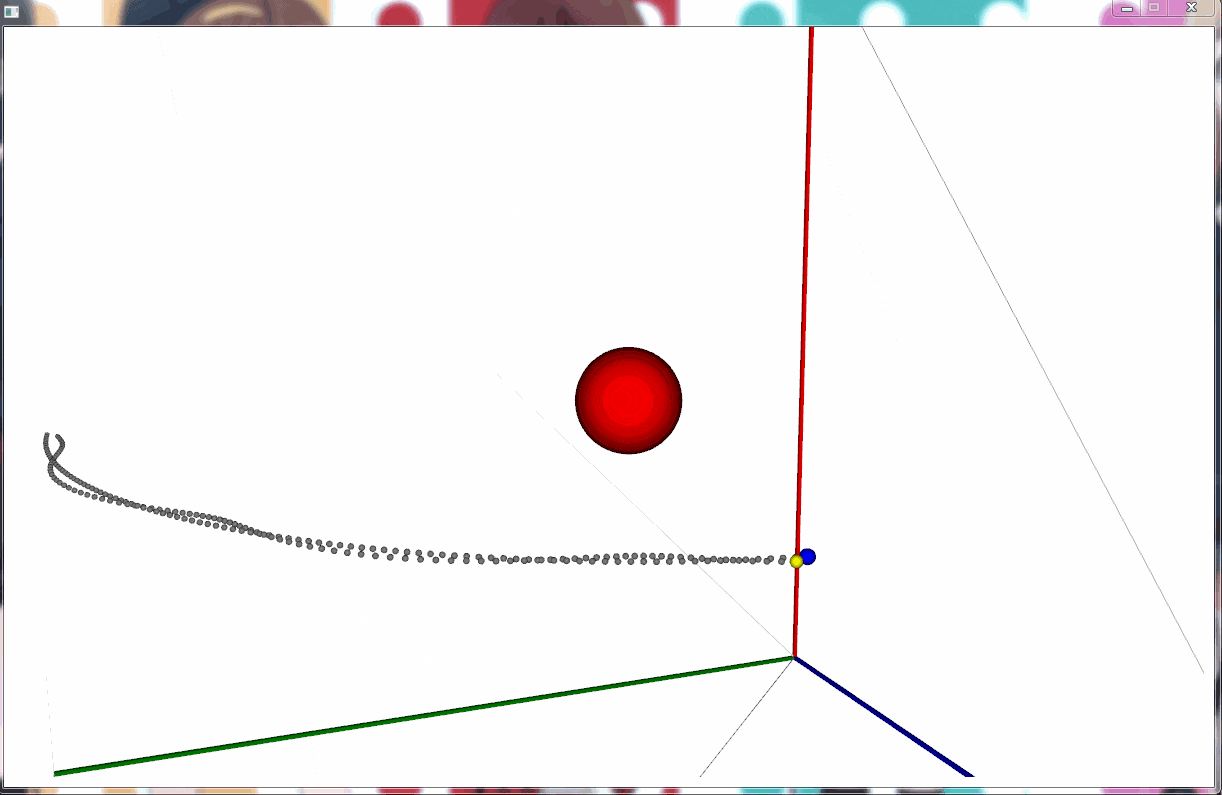
綺麗に円運動しているように見える。

しかし、よーく見てみると少しずつだが円の半径が大きくなっている。
正確な原因は分からないが、 double による計算に誤差があるのかもしれない。

まぁ、それっぽく動いてるので良しということで。

#振り子
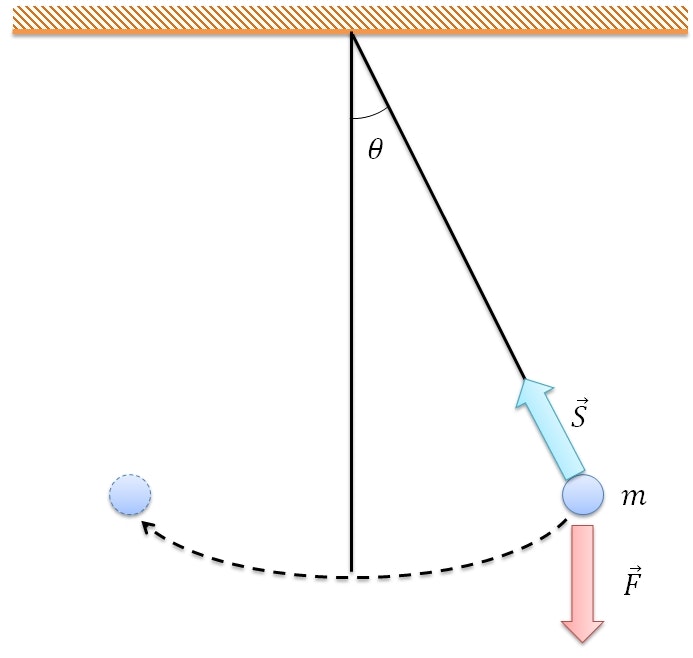
天井から紐で物体を吊るし手を放すと、紐の長さを半径とする円弧上を物体が行ったり来たりする。
これを振り子と呼ぶ。

##物体に働く力を洗い出す
物体には次の２つの力が作用している。

物体に働く重力 $\vec{F}$
紐が物体を引っ張る張力 $\vec{S}$

それぞれの求め方を考える。

重力は単純に、以下の式で求まる。

\vec{F} = m\vec{g}

次に張力。
張力には、重力が物体を引っ張ることによって発生する反作用の分（$\vec{S_g}$）と、円運動を支えるための向心力（$\vec{S_c}$）とが含まれる。

まずは、重力に起因する張力を考える。
これは、物体にかかる重力を糸と同じ方向に分けた成分の反作用と考えられる。

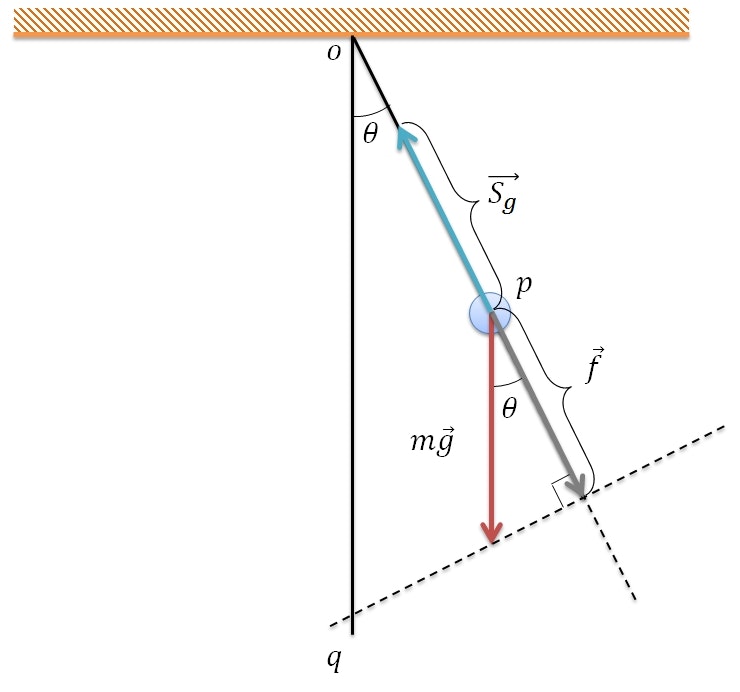
図にすると以下のような感じ。

灰色のベクトル $\vec{f}$ が、物体が糸を引く力で、張力 $\vec{S_g}$ はその反対向きになる。

$\vec{f}$ の大きさは $m|\vec{g}|\cos\theta$ で求まる。
また $\vec{f}$ の向きはベクトル $\vec{op}$ と同じなので、その単位ベクトル（$\frac{\vec{op}}{|\vec{op}|}$）を求めて↑の大きさを掛ければ $\vec{f}$ が求まる。

\vec{f} = m|\vec{g}|\cos\theta\frac{\vec{op}}{|\vec{op}|}

張力 $\vec{S_g}$ は $\vec{f}$ の逆ベクトルなので、

\begin{eqnarray}
\vec{S_g} & = & -\vec{f} \\
          & = & -m|\vec{g}|\cos\theta\frac{\vec{op}}{|\vec{op}|}
\end{eqnarray}

となる。

ここで、 $\theta$ はベクトル $\vec{oq}$ と $\vec{op}$ の成す角なので、以下の式が成り立つ。

\cos\theta = \frac{\vec{oq} \cdot \vec{op}}{| \vec{oq} | | \vec{op} |}

※ベクトルのなす角 | KIT数学ナビゲーション

座標 $q$ は $o$ の真下の任意の点で良いので、計算しやすいように $q = (o_x, o_y - 1, o_z)$ と定義する。
すると、 $\vec{oq} = (0, -1, 0)$ となり、 $| \vec{oq} | = 1$ となる。
これを上の式に反映すると、

\begin{eqnarray}
\cos\theta & = & \frac{\vec{oq} \cdot \vec{op}}{| \vec{oq} | | \vec{op} |} \\
           & = & \frac{(0, -1, 0) \cdot (op_x, op_y, op_z)}{1 \times | \vec{op} |} \\
           & = & \frac{0 \times op_x + (-1) \times op_y + 0 \times op_z}{| \vec{op} |} \\
           & = & \frac{-op_y}{| \vec{op} |}
\end{eqnarray}

この結果を、先ほどの力 $\vec{S_g}$ を求める式に代入する。

\begin{eqnarray}
\vec{S_g} & = & -m|\vec{g}|\cos\theta\frac{\vec{op}}{|\vec{op}|} \\
          & = & -m|\vec{g}|\frac{-op_y}{| \vec{op} |}\frac{\vec{op}}{|\vec{op}|} \\
          & = & \frac{m|\vec{g}| op_y}{| \vec{op} |^2}\vec{op}
\end{eqnarray}

最後に円運動による向心力 $\vec{S_c}$ を求める。

向心力は、円運動のときにも使った以下の式を利用する。

|\vec{F}| = m\frac{|\vec{v}|^2}{r}

今回の場合、半径 $r$ はベクトル $\vec{op}$ の大きさに等しいので、

|\vec{F}| = m\frac{|\vec{v}|^2}{|\vec{op}|}

張力 $\vec{S_c}$ は、$\vec{op}$ の単位ベクトル（$\frac{\vec{op}}{|\vec{op}|}$）に↑の大きさを掛けたものの逆ベクトルになるので、

\begin{eqnarray}
\vec{S_c} & = & -m\frac{|\vec{v}|^2}{|\vec{op}|}\frac{\vec{op}}{|\vec{op}|} \\
          & = & -\frac{m|\vec{v}|^2}{|\vec{op}|^2}\vec{op}
\end{eqnarray}

ということで、最終的に求めたい張力 $\vec{S}$ は、これらの合力なので、

\begin{eqnarray}
\vec{S} & = & \vec{S_g} + \vec{S_c} \\
        & = & \frac{m|\vec{g}| op_y}{| \vec{op} |^2}\vec{op} -\frac{m|\vec{v}|^2}{|\vec{op}|^2}\vec{op} \\
        & = & \frac{m(|\vec{g}|op_y - |\vec{v}|^2)}{|\vec{op}|^2}\vec{op}
\end{eqnarray}

ということで、物体に働く力はわかったので、実装してみる。

##張力を実装する

Tension.java

package gl8080.physics.domain.force;

import java.util.Objects;

import gl8080.physics.domain.ActingForce;
import gl8080.physics.domain.Physical;
import gl8080.physics.domain.primitive.Force;
import gl8080.physics.domain.primitive.Point;
import gl8080.physics.domain.primitive.Vector;
import gl8080.physics.domain.primitive.Velocity;

public class Tension implements ActingForce {
    
    private final Point fixdPoint;
    
    public Tension(Point fixdPoint) {
        Objects.requireNonNull(fixdPoint);
        this.fixdPoint = fixdPoint;
    }

    @Override
    public Force getForce(Physical target) {
        // 重力と
        Force gravityForce = this.calcGravityForce(target);
        // 張力を求めて
        Force tensionForce = this.calcTensionForce(target);
        
        // ２つの合力を返す
        return gravityForce.add(tensionForce);
    }

    private Force calcGravityForce(Physical target) {
        return new Force(0.0, target.getMass().quantity * -9.8, 0.0);
    }

    private Force calcTensionForce(Physical target) {
        double m = target.getMass().quantity;
        double g = 9.8;
        Vector op = Vector.create(this.fixdPoint, target.getLocation());
        Velocity v = target.getVelocity();
        double vv = v.x*v.x + v.y*v.y + v.z*v.z;
        double opop = op.x*op.x + op.y*op.y + op.z*op.z;
        
        double k = m * (g*op.y - vv) / opop;
        
        double fx = k * op.x;
        double fy = k * op.y;
        double fz = k * op.z;
        
        return new Force(fx, fy, fz);
    }
}

計算結果をそのまま実装に落とした感じ。

とりあえず動かしてみる。

Main.java

package gl8080.physics;

// ...

public class Main extends Application {
    
    // ...

    public Parent createContent() throws Exception {
        // ボールを作る
        Mass mass = new Mass(10.0); // 質量
        Point location = new Point(80.0, 40.0, 20.0); // 初期位置
        Velocity velocity = Velocity.ZERO; // 速度
        Ball ball = new Ball(mass);
        ball.setLocation(location);
        ball.setVelocity(velocity);
        
        // 実験空間の用意
        // ...
        
        // ボールのシェイプを作り、空間に追加する
        // ...
        
        // 物理法則を作り、力に張力を設定
        Point center = new Point(50.0, 100.0, 50.0);
        ActingForce actingForce = new Tension(center);
        PhysicalLaw law = new LawOfMotion(actingForce);
        
        // 軌跡
        // ...

        // 世界を作り、ボールと物理法則を追加する
        // ...
        
        // 時の流れをスタートさせる
        // ...
    }
}

思いの外それっぽく動いた。

ちなみに、これも実は徐々に半径が長くなっていたりするけど、それっぽいので（ｒｙ

#万有引力
最後は万有引力を実装してみる。

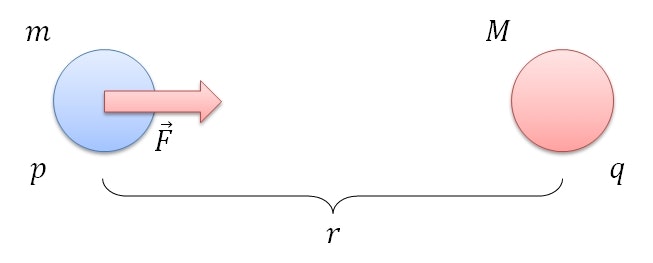
万有引力とは、質量を持つ物体の間に働く力で、互いの質量に比例し距離の二乗に反比例する。

式で表現すると、以下のようになる。

\vec{F} = G\frac{Mm}{r^2}\frac{\vec{pq}}{|\vec{pq}|}

$G$ は万有引力定数でおよそ $6.67 \times 10^{-11}$、 $M$ と $m$ は物体の質量、 $r$ は物体間の距離を表している。

##トランザクション的な制御の追加
式自体は単純なので力を計算する実装はすぐできる。
しかし、力を使って次の位置と速度を計算する実装に、現状では問題がある。

現状では、物体１つ１つに対して順次計算結果を反映している。
しかし、万有引力の大きさは、物体のお互いの位置に依存している。つまり、先に一方の位置を更新してしまうと、次に相手側の万有引力の大きさを計算するときに距離が縮まってしまい本来よりも大きな力を算出してしまう。

これを回避するため、計算結果の反映を後回しにする仕組みを追加する必要がある。
丁度、 RDB のトランザクションみたいな仕組みになる。

###実装方法
実装は以下のようなイメージ。

「世界」に「物体」を追加するときに、「トランザクション可能な物体」で内部的にラップしてあげて、トランザクション的な制御を行えるようにする。
こうすれば、利用する側は変更を加えなくて済む。

###実装する

TransactionalPhysical.java

package gl8080.physics.domain.physical;

import java.util.Objects;

import gl8080.physics.domain.Physical;
import gl8080.physics.domain.primitive.Mass;
import gl8080.physics.domain.primitive.Point;
import gl8080.physics.domain.primitive.Velocity;

public class TransactionalPhysical implements Physical {
    
    private final Physical original;
    private Point location;
    private Velocity velocity;
    
    public TransactionalPhysical(Physical original) {
        Objects.requireNonNull(original);
        this.original = original;
    }
    
    public void commit() {
        if (this.location != null) {
            this.original.setLocation(location);
        }
        
        if (this.velocity != null) {
            this.original.setVelocity(velocity);
        }
    }

    @Override
    public Velocity getVelocity() {
        return this.original.getVelocity();
    }

    @Override
    public Point getLocation() {
        return this.original.getLocation();
    }

    @Override
    public Mass getMass() {
        return this.original.getMass();
    }

    @Override
    public void setLocation(Point location) {
        this.location = location;
    }

    @Override
    public void setVelocity(Velocity velocity) {
        this.velocity = velocity;
    }
}

セッターメソッドは受け取った値をインスタンスフィールドに記録しておき、 commit() のタイミングで変更を反映するようにしている。
ゲッターメソッドは、オリジナルの Physical にそのまま処理を委譲している。

World.java

package gl8080.physics.domain;

import java.util.HashSet;
import java.util.Objects;
import java.util.Set;
import java.util.stream.Collectors;

import gl8080.physics.domain.physical.TransactionalPhysical;

public class World {
    
    private Set<TransactionalPhysical> physicals = new HashSet<>();
    private Set<PhysicalLaw> physicalLaws = new HashSet<>();
    
    void next(double sec) {
        this.physicals.forEach(physical -> {
            this.physicalLaws.forEach(law -> {
                law.apply(physical, sec);
            });
        });
        
        // ★最後にコミット
        this.physicals.forEach(physical -> {
            physical.commit();
        });
    }
    
    public void addPhysical(Physical physical) {
        Objects.requireNonNull(physical);
        this.physicals.add(new TransactionalPhysical(physical)); // ★TransactionalPhysical でラップ
    }
    
    // ...
}

##万有引力の実装

package gl8080.physics.domain.force;

import java.util.Objects;
import java.util.Set;

import gl8080.physics.domain.ActingForce;
import gl8080.physics.domain.Physical;
import gl8080.physics.domain.World;
import gl8080.physics.domain.primitive.Force;
import gl8080.physics.domain.primitive.Vector;

public class UniversalGravitation implements ActingForce {
    
    private static final double G = 6.67 * Math.pow(10.0, -11.0);
    private final World world;
    
    public UniversalGravitation(World world) {
        Objects.requireNonNull(world);
        this.world = world;
    }

    @Override
    public Force getForce(Physical target) {
        // ★他の物体を全て取得
        Set<Physical> others = this.world.getPhysicalsWithout(target);
        
        // ★それぞれの物体間に働く万有引力を計算して、合計を計算する
        return others.stream()
                     .map(other -> this.calcForce(target, other))
                     .reduce(Force.ZERO, (f1, f2) -> f1.add(f2));
    }
    
    private Force calcForce(Physical me, Physical other) {
        Vector vector = Vector.create(me.getLocation(), other.getLocation());
        double rr = vector.x*vector.x + vector.y*vector.y + vector.z*vector.z;
        double m = me.getMass().quantity;
        double M = other.getMass().quantity;
        
        double F = G * M * m / rr;
        
        Vector f = vector.normalize().multiply(F);
        
        return new Force(f.x, f.y, f.z);
    }
}

動作確認。

Main.java

package gl8080.physics;

// ...

public class Main extends Application {
    
    // ...

    public Parent createContent() throws Exception {
        // 実験空間の用意
        final double size = 100;
        Space space = new Space(size, new Camera());
        space.add(new Axis(size));

        // 世界を作り、ボールと物理法則を追加する
        World world = new World();
        
        // ボール１を作る
        createBall()
            .mass(100.0)
            .location(55, 50, 50)
            .velocity(0, 0, 0)
            .radius(1.0)
            .color(Color.RED)
            .appendTo(world, space);
        
        // ボール２を作る
        createBall()
            .mass(100.0)
            .location(45, 50, 50)
            .velocity(0, 0, 0)
            .radius(1.0)
            .color(Color.BLUE)
            .appendTo(world, space);
        
        // 物理法則を作り、力に万有引力を設定
        ActingForce actingForce = new UniversalGravitation(world);
        PhysicalLaw law = new LawOfMotion(actingForce);
        
        // 軌跡
        // ...
        
        // 時の流れをスタートさせる
        // ...
    }
    
    private static BallAppender createBall() {
        return new BallAppender();
    }
    
    private static class BallAppender {
        // ビルダーパターンで実装
    }
}

「物体」（ボール）を２つ作成して配置している。
処理が重複するので、ビルダーで配置できるようにリファクタリングした。

動かない。。。

##距離の比率・時間の早さを調整する
それもそのはずで、万有引力というのは非常に力が小さい。
万有引力定数が $6.67 \times 10^{-11} = 0.0000000000667$ と非常に小さい値なので、これを打ち消せるほどの質量（天体レベルの質量）がないと目に見える力にならない。

しかし、単純に質量を天体レベルに引き上げてしまうと、現状の仮想空間のサイズ（１辺 $100m$）では狭すぎてまともな観察ができない。
ということで、天文学レベルの距離を扱えるようにドメインが扱う位置（Point）と、 3D 空間で扱う位置を別のクラスに分離し、比率を指定して相互変換できるようにする。

ViewPoint.java

package gl8080.physics.view;

import gl8080.physics.domain.primitive.Point;

public class ViewPoint {
    // ★比率
    public static double RATE = 1.0;
    
    public final double x;
    public final double y;
    public final double z;
    
    // ★実座標を 3D 空間で扱うための座標に変換する
    public static ViewPoint of(Point p) {
        return new ViewPoint(p.x * RATE, p.y * RATE, p.z * RATE);
    }

    public ViewPoint(double x, double y, double z) {
        this.x = x;
        this.y = y;
        this.z = z;
    }
    
    // ★3D 空間での座標を、実座標に変換する
    public Point toPoint() {
        return new Point(this.x / RATE, this.y / RATE, this.z / RATE);
    }
    
    // ...
}

運動の演算は Point で行い、画面に表示するときは ViewPoint に変換して描画させる。

これで空間の狭さの問題は解決するが、まだ時間の問題が残っている。
例えば太陽の回りを公転する地球をシミュレーションしようとすると、１回転するのを観察するのに１年かかってしまう。

つまり、観察しやすいようにするため時間を早く進められるようにしないといけない。

時間の制御は Time クラスのお仕事なので、 Time クラスを修正する。

Time.java

package gl8080.physics.domain;

import java.util.Objects;

public class Time {

    // ...
    private int speed;
    
    public Time(World world, int speed) {
        Objects.requireNonNull(world);
        this.world = world;
        this.speed = speed;
    }
    
    public Time(World world) {
        this(world, 1);
    }
    
    public void start() {
        while (this.isContinued) {
            for (int i=0; i<this.speed; i++) { // ★ここで調整
                this.world.next(FRAME_LATE);
            }
            this.sleep(FRAME_LATE);
        }
    }
    
    // ...
}

speed で指定した回数だけ多く計算をすることで、時間を調整する。

##描画頻度の調整
さらに、現状だと Physical#setLocation() するたびに画面を再描画しているが、これだと再描画回数が多すぎて表示が間に合わなくなる（表示が更新されなくなる）。
なので、 Physical ごとにリスナーを設定して再描画をしている現行の実装を廃止して、 Time が１回時間を進めるごとに全 Content を再描画するように修正する。

Time.java

package gl8080.physics.domain;

import java.util.Objects;

public class Time {

    // ...
    private Runnable tick = () -> {};
    
    // ...
    
    public void start() {
        while (this.isContinued) {
            for (int i=0; i<this.speed; i++) {
                this.world.next(FRAME_LATE);
            }
            this.tick.run(); // ★コールバック
            this.sleep(FRAME_LATE);
        }
    }
    
    public void setTick(Runnable tick) {
        Objects.requireNonNull(tick);
        this.tick = tick;
    }

    // ...
}

Main.java

package gl8080.physics;

// ...

public class Main extends Application {
    
    // ...

    public Parent createContent() throws Exception {
        // ...
        
        // 時の流れをスタートさせる
        this.time = new Time(world, 50000);
        this.time.setTick(() -> {
            space.refresh(); // ★時間が進む毎に再描画を実行
        });
        
        // ...
    }
    
    // ...
}

Space.java

package gl8080.physics.view;

// ...

public class Space {
    
    private Set<Content> contents = new HashSet<>();

    // ...

    public void add(Content content) {
        // ...
        this.contents.add(content);
    }
    
    // ...

    public void refresh() {
        this.contents.forEach(Content::refresh); // ★全 Content を再描画させる
    }
}

BallShape.java

package gl8080.physics.view.shape;

// ...

public class BallShape implements Content {
    
    // ...
    private Ball ball;

    public BallShape(Ball ball, double radius, Color color) {
        // ...
        this.ball = ball;
    }

    // ...
    @Override
    public void refresh() {
        Point location = this.ball.getLocation(); // ★現在位置を取得して
        this.translate(location); // ★再描画
    }
}

##冥王星とカロンっぽい動き
2015/07/14 にニュー・ホライズンズが再接近に成功したことで話題になった冥王星。
それと、その衛星であるカロンの物理量を設定して動きを見てみる。

Main.java

package gl8080.physics;

// ...

public class Main extends Application {
    
    // ...

    public Parent createContent() throws Exception {
        // 一辺が 5万km になるように縮尺を設定
        ViewPoint.RATE = 0.2 * Math.pow(10, -5);
        
        // 実験空間の用意
        // ...

        // 世界作る
        // ...
        
        // 冥王星
        createBall()
            .mass(1.3 * Math.pow(10, 22))
            .locationKm(25000, 25000, 25000)
            .velocityKm(0, 0, -0.02)
            .radius(2.0)
            .color(Color.RED)
            .appendTo(world, space);
        
        // カロン
        createBall()
            .mass(1.52 * Math.pow(10, 21))
            .locationKm(25000 + 19571, 25000, 25000)
            .velocityKm(0, 0, 0.185)
            .radius(1.0)
            .color(Color.BLUE)
            .appendTo(world, space);
        
        // 物理法則を作り、力に万有引力を設定
        ActingForce actingForce = new UniversalGravitation(world);
        PhysicalLaw law = new LawOfMotion(actingForce);
        
        // 軌跡
        // ...
        
        // 時の流れをスタートさせる
        this.time = new Time(world, 60000); // ★ 6万倍の早さで時を進める
        // ...
    }
    
    // ...
}

質量と距離は Wikipedia の情報を元に設定。
初速度はそれっぽく動くように手調整したので、特に根拠はない。

質量

星	質量
冥王星	$1.3 \times 10^{22} kg$
カロン	$1.52 \times 10^{21} kg$

距離

$19,571 km$

それっぽい動きをしている。
軌道の中心が冥王星の中にはなく、カロン側にズレた場所にあるのが分かる。

##太陽と彗星っぽい動き
彗星っぽい楕円軌道。

Main.java

package gl8080.physics;

// ...

public class Main extends Application {
    
    // ...

    public Parent createContent() throws Exception {
        final double size = 100;
        
        // 一辺が 50,000km になるように縮尺を設定
        ViewPoint.setRate(size, 50_000.0);
        
        // 実験空間の用意
        // ...

        // 世界を作り、ボールと物理法則を追加する
        // ...

        // 星１
        createBall()
            .mass(1.0 * Math.pow(10, 23))
            .locationKm(25000, 25000, 25000)
            .velocityKm(0, 0, 0)
            .radius(5.0)
            .color(Color.RED)
            .appendTo(world, space);
        
        // 星２
        createBall()
            .mass(1.0 * Math.pow(10, 10))
            .locationKm(50000, 50000, 50000)
            .velocityKm(-0.1, 0, 0.2)
            .radius(1.0)
            .color(Color.BLUE)
            .appendTo(world, space);
        
        // 物理法則を作り、力に万有引力を設定
        // ...
        
        // 軌跡
        BallLocus locus = BallLocus.create(law).historySize(100).interval(100000).radius(0.5).build();
        space.add(locus);
        world.addPhysicalLaws(locus);
        
        // 時の流れをスタートさせる
        // ...
    }
    
    // ...
}

##恒星と惑星と衛星
恒星を公転する惑星と、惑星を公転する衛星みたいな。

Main.java

package gl8080.physics;

// ...

public class Main extends Application {
    
    // ...

    public Parent createContent() throws Exception {
        final double size = 100;
        
        // 一辺が 30,000,000km になるように縮尺を設定
        ViewPoint.setRate(size, 30_000_000);
        
        // 実験空間の用意
        // ...

        // 世界を作り、ボールと物理法則を追加する
        // ...

        // 恒星
        createBall()
            .mass(1.0 * Math.pow(10, 30))
            .locationKm(15_000_000, 15_000_000, 15_000_000)
            .velocityKm(0, 0, 0)
            .radius(5.0)
            .color(Color.RED)
            .appendTo(world, space);
        
        // 惑星
        createBall()
            .mass(1.8986 * Math.pow(10, 27))
            .locationKm(30_000_000, 15_000_000, 15_000_000)
            .velocityKm(0, 0, -67)
            .radius(0.5)
            .color(Color.BLUE)
            .appendTo(world, space);
        
        // 衛星
        createBall()
            .mass(8.9 * Math.pow(10, 22))
            .locationKm(29_600_000, 15_000_000, 15_000_000)
            .velocityKm(0, 0, -50)
            .radius(0.4)
            .color(Color.YELLOW)
            .appendTo(world, space);
        
        // 物理法則を作り、力に万有引力を設定
        // ...
        
        // 軌跡
        BallLocus locus = BallLocus.create(law).historySize(100).color(Color.GRAY).interval(100000).radius(0.2).build();
        space.add(locus);
        world.addPhysicalLaws(locus);
        
        // 時の流れをスタートさせる
        // ...
    }
    
    // ...
}

これの調整が難しかった。
だが、おもしろい。。。

#まとめ
運動方程式で、確かに日常の運動から天体の動きまでそれっぽい動きを再現できた（力の計算はいろいろ切り替えたが、 LawOfMotion は変更していない！）。
高校物理（というか力学）おもしろい。

プログラミングと物理シミュレーションを合わせた授業とかが高校のときにあったら、面白かったかもしれない。

#参考

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up