二分法（非線形方程式の数値解法）

二分法とは

• 非線形方程式の数値解法の一つ
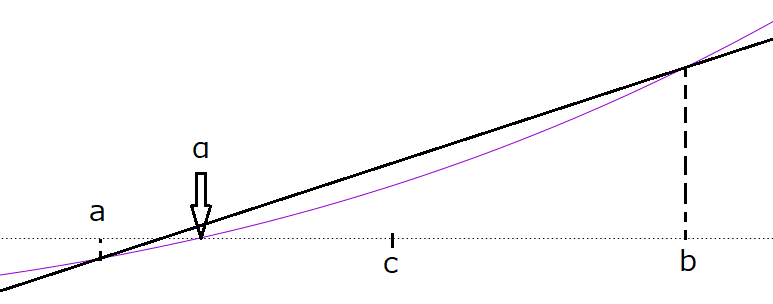
• 中間値の定理 : 閉区間$[a,b]$で連続な関数$f(x)$において、$f(a)f(b)<0$ ならば、$f(\alpha)=0$ なる$\alpha$は区間$[a,b]$内に存在する
• $f(a)f(b)<0$となる $a,b$ を見つけ、中点$c=(a+b)/2$を新しい端点として計算を繰り返す。

算法

初期値

$x_{a_0},x_{b_0}$ : 適当な方法で決める。ただし、$f(x_{a_0})f(x_{b_0})<0$

反復手順

$x_{c_n}=(x_{a_n}+x_{b_n})/2$ $,$ $(n=1,2,\cdots)$
$f(x_{c_n})f(x_{a_n})<0$ ならば、$x_{a_{n+1}}=x_{a_n}$ $,$ $x_{b_{n+1}}=x_{c_n}$
$f(x_{c_n})f(x_{a_n})>0$ ならば、$x_{a_{n+1}}=x_{c_n}$ $,$ $x_{b_{n+1}}=x_{b_n}$

停止則

$|x_{a_n}-x_{b_n}|<\varepsilon$ のとき反復停止
ただし、$\varepsilon$ は適当に与える。

サンプルコード

$f(x)=x^2-1$ 、初期値 $a=0.5,b=2$として二分法を使って解を求めるプログラム。
$f(a)f(b)<0$ の確認とか入れてないガバガバコード

bisection_method.c

#include<stdio.h>
#include<math.h>

double f (double x) {
  return x*x-1;
}

double bisection_method (double a, double b) {
  double c;
  while (fabs(a - b) > 1e-10) {
    c = (a + b) / 2;
    if (f(c) == 0) { break; }
    if (f(a) * f(c) < 0) { b = c; }
    if (f(a) * f(c) > 0) { a = c; }
  }
  return c;
}

int main (void) {
  double alpha;
  alpha = bisection_method(0.5, 2);
  printf("%f\n", alpha);
  return 0;
}

実行結果

1.000000

特徴

• $f^{\prime}(x)$の計算不要
  • 簡単、直感的
• 必ず解に収束
  • 連続であれば必ず解に収束
• 誤差は区間幅以下（$|x_b-x_a|$）
• 初期値2つ必要
• Newton法、割線法に比べ、反復回数が増加
• 収束の速さ：1次
  • 一回の計算で区間が半分になる=誤差が半分になる