C言語でヒープソート

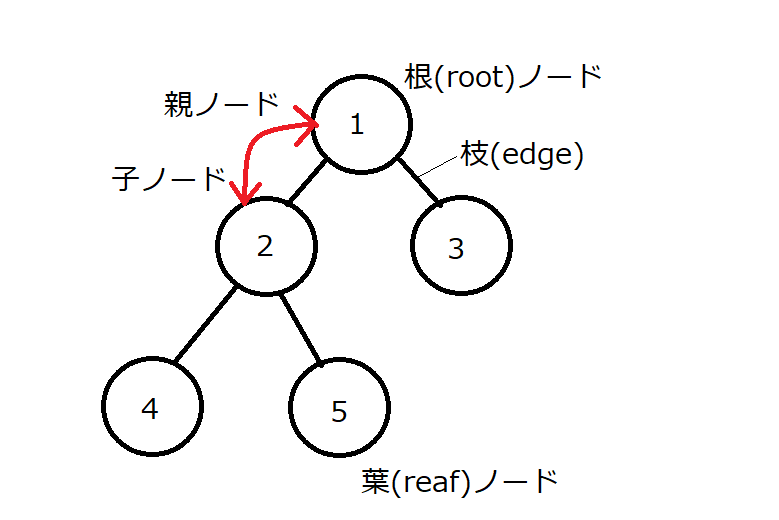
ヒープとは

• 半順序集合をツリーで表現したデータ構造
  • 「親ノードは子ノードよりも小さい（もしくは大きい）か等しい」という条件を満たすツリー構造
• 一般にヒープといったら二分木を意味する

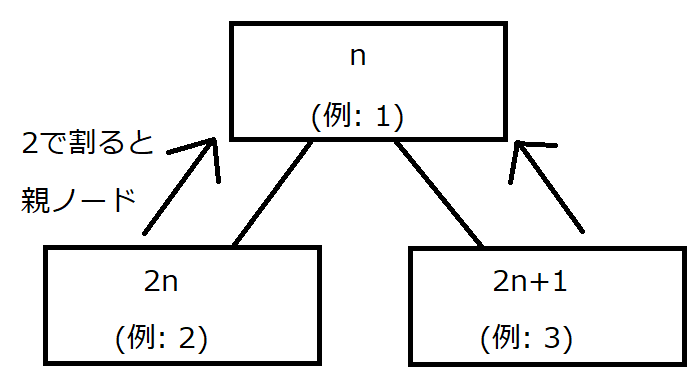
配列を使ったヒープの実現

インデックスを $1$ から開始すると、ノード $n$ の親ノードは $n/2$、子ノードは $2n$ と $2n+1$ でアクセスできる。
ただし、親ノードのインデックスを計算する除算は小数点以下切り捨て

※インデックスを$0$から開始すると、ノード $n$ の親ノードは $(n-1)/2$、子ノードは $2n+1$ と $2n+2$

ヒープソートとは

1. 要素数 $N$ のヒープを、「子よりも親が大きい」として構築：根が最大値となる

2. 根を配列の最後尾と入れ替える。

3. $N-1$ 個の要素のヒープを構築しなおす：根が2番目に大きい値となる

   $\vdots$

ヒープの再構築

根を配列の後ろの要素と入れ替えた後は、先頭要素（根）を除いてヒープ構造ができている。
次の手順を、根ノードから開始

1. 大きいほうの子と比較
2. 親が大きければヒープ構築済み
3. 親が小さければ子と入れ替えて、さらに下の子と比較

自分より大きな子と入れ替えて、自身を下に下げながらヒープを構築する位置までおろしていく：pushdown操作

配列全体のヒープ化

ヒープソートを行うには、配列がヒープ構造になっていることが前提

• 下から、ボトムアップ的にヒープ化する
• pushdown操作を使ってヒープ化できる
  • 要素 $N$ とすると、最初に $N/2$ (最後のノードの親)をヒープ化する
  • $N/2,N/2-1,N/2-2,\cdots,2,1$ の順にpushdownしていく

サンプルコード

ここでは、int型の配列を、ヒープソートを用いて小さい順に整列する。
※整列する部分は配列の添え字が1から10までです。

heap_sort.c

#include<stdio.h>

/* 値を入れ替える関数 */
void swap (int *x, int *y) {
  int temp;    // 値を一時保存する変数

  temp = *x;
  *x = *y;
  *y = temp;
}

/* pushdouwn操作 */
void pushdown (int array[], int first, int last) {
  int parent = first;   // 親
  int child = 2*parent;   // 左の子
  while (child <= last) {
    if ((child < last) && (array[child] < array[child+1])) {
       child++;   // 右の子の方が大きいとき、右の子を比較対象に設定
    }
    if (array[child] <= array[parent]) { break; }   // ヒープ済み
    swap(&array[child], &array[parent]);
    parent = child;
    child = 2* parent;
  }
}

/* ヒープソート */
void heap_sort (int array[], int array_size) {
  int i;

  for (i = array_size/2; i >= 1; i--) {
    pushdown(array, i, array_size);   // 全体をヒープ化
  }
  for (i = array_size; i >= 2; i--) {
    swap(&array[1], &array[i]);   // 最大のものを最後に
    pushdown(array, 1, i-1);   // ヒープ再構築
  }
}

int main (void) {
  int array[11] = { 0, 2, 1, 8, 5, 4, 7, 9, 10, 6, 3 };
  int i;

  printf("Before sort: ");
  for (i = 1; i < 11; i++) { printf("%d ", array[i]); }
  printf("\n");

  heap_sort(array, 10);

  printf("After sort: ");
  for (i = 1; i < 11; i++) { printf("%d ", array[i]); }
  printf("\n");

  return 0;
}

実行結果

Before sort: 2 1 8 5 4 7 9 10 6 3
After sort: 1 2 3 4 5 6 7 8 9 10

性能

• 先頭要素を取り出すだけで最大値を求めることができる
• 残った要素を再ヒープ化する必要がある
  • この計算量は$O(\log{n})$
• この操作を全要素に対して行うので、全体としての計算量は$O(n\log{n})$
• 作業領域を節約できるので、効率のいいソートが実現可能
  • 整列のための特別な作業領域を必要としない
  • クイックソートのような再帰処理を必要としない