2016/04/04追記 ここで挙げているコードを参考にする際は、以下の点に注意してください(八田さん、Pocolさん、西山さん、qさんフィードバックありがとうございます)
※コピペしてコンパイルするとコンパイルエラー出ます。ちゃんと確認していないですがstlのメソッド名が間違っているようです
※SAHによるソートが遅いです。ソートに関してはPBRTに書かれているようなので参考にしてください(std::partitionを使うらしいです)
※SHAの計算は定義にバカ正直に当てはめていますが、値の比較しかしないのでいくつかの計算が省略できます
※上記の点についての修正は、気が向いたらやります。やらないかもしれません。
この Qiita というサービスが流行っているようなので、はてダのかわりに試しに投稿してみます。
と思ったのですが、アップロード可能な画像が月間2MBとちょっと辛いので、またはてダに戻るかもしれません。。。
レイトレで複雑なモデルの描画
以前はてダにちょろっと書いた edupt ベースのレンダラ (http://d.hatena.ne.jp/omochi64/20131205/1386251942) ですが、これには obj ファイルの簡単なローダを実装しており、三角形ポリゴンで構成されたモデルを描画することもできます。
できるのですが、ポリゴンの数が多いモデルをレンダリングしようと思うと、 edupt がやっているようにレイの交差判定をすべてのオブジェクトと行うのではあまりに時間がかかりすぎてしまいます。
そこで、効率よく交差判定を行うため、モデルの領域分割処理を行うのが一般的です。
領域分割の方法にはいろいろなものがありますが、レイトレでは kd-tree や Bounding Volume Hierarchy (BVH) がよく用いられます。
今回は BVH を実装したので、BVH とは何か、BVH の構築方法、BVH を用いたレイの交差判定処理について、コードを交えながら説明します。
Bounding Volume Hierarchy とは
BVH は、与えられたポリゴン群を囲う AABB (Axis Aligned Bounding Box) の中に、それらのポリゴンを2つのグループに分割し、それぞれを囲う AABB が入っている構造となります。
(AABB はXYZ軸に沿った直方体のことです)
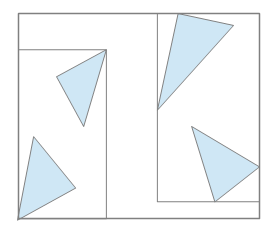
実際には、これを2つのそれぞれの AABB の中でさらに2つに分割して、そのまた中でさらに分割して、…と、再帰的に分割処理を行うことで二分木構造にしたものを使います。
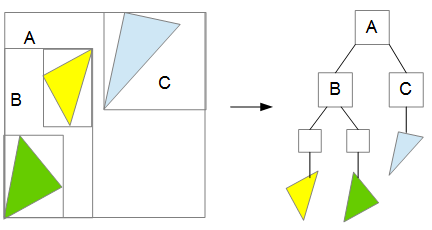
とてもシンプルなことに、定義上の BVH の簡単な説明はこれでおしまいです。
BVH のメリット・デメリット
BVH だけでなく kd-tree などもそうですが、レイとの交差判定を行う回数が劇的に減る点がメリットとなります。
たとえば先ほどの図で、レイが A と C のAABBにしか交差しなかった場合、B より下の AABB やポリゴンと交差判定を行う必要がなくなります (親ノードのAABBは必ず子ノードのAABBを内包している)。
単純にシーン中の全オブジェクトと交差判定をした場合、その計算量は $O(mn)$ ($m$ はレイの数、$n$ はオブジェクトの数)となりますが、BVH の場合、$O(m\log(n))$となります。log オーダーなので速いです。
しかし、線形探索の時には必要なかった「BVHの構築」という構築処理が必要となってきます。
特に動的なシーンをレンダリングする際は、この構築時間がとても重要になります。
この構築時間を短縮するための研究もいろいろとありますが、今回はそれには触れず (というかよく知らない) に基本的なことのみ紹介していきます。
BVH の構築
BVH を構築する際、「どのように与えられたポリゴンを2つに分けるか」という点が重要になります。
単純には、XYZ軸のうち適当な軸を1つ取ってきて、その軸で AABB をちょうど半分にするように分けたり、ポリゴンの数が左右で同数になるように分けたり、という方法があります。
私が実装したのは SAH (Surface Area Heuristics) という手法で、上記のような単純な手法より効率が良くなるようです。
BVH における SAH では、次のようなコスト関数を最小化するように分割を行います。
(※(Ingo and et al., 2007) からこのように理解しましたが、もし私の理解が間違っていたら詳しい人教えてください)
T = 2T_{AABB} + \frac{A(S_1)}{A(S)}N(S_1)T_{tri} + \frac{A(S_2)}{A(S)}N(S_2)T_{tri}
数式が出てきて面食らったかもしれないですが、実際はそんなに大した式ではないです。
$T_{AABB}$ は AABB とレイの交差判定にかかるコスト (時間)、$T_{tri}$ はポリゴンとレイの交差判定にかかるコスト、$A(S), A(S_1), A(S_2)$ は、領域全体を囲うAABBの表面積、2つに分割された領域$S_1, S_2$を囲う AABB の表面積を表し、$N(S_1), N(S_2)$ は $S_1, S_2$ 内にあるポリゴンの数、となります。
つまり、
2×AABBの交差判定にかかる時間 + (領域1のAABBの表面積×領域1のポリゴンの数 + 領域2のAABBの表面積×領域2のポリゴンの数) × ポリゴンの交差判定にかかる時間 / 領域全体のAABBの表面積
これが最小となる領域1と2の分け方を見つけることになります。
これに従って領域を2つに分割し、その分割された2つの領域内で再帰的に分割処理を行うことで BVH が構築されます。
それでは続いて、better Cなコードで構築部分を書いていきます。
結構長くなってしまったので、全体のコードを示した後、部分部分で説明します。
// BVH のノードの構造
struct BVH_node {
float bbox[2][3]; // bbox[0,1]: AABB の最小,最大座標. bbox[hoge][0,1,2]: x,y,z座標
int children[2]; // 子ノード
vector<Triangle *> polygons; // 格納されているポリゴン (葉ノードのみ有効)
};
// AABB の表面積計算
float surfaceArea(const float bbox[2][3]) {
float dx = bbox[1][0] - bbox[0][0];
float dy = bbox[1][1] - bbox[0][1];
float dz = bbox[1][2] - bbox[0][2];
return 2*(dx*dy + dx*dz + dy*dz);
}
// 空の AABB を作成
void emptyAABB(float bbox[2][3]) {
bbox[0][0] = bbox[0][1] = bbox[0][2] = INF;
bbox[1][0] = bbox[1][1] = bbox[1][2] = -INF;
}
// 2つのAABBをマージ
void mergeAABB(const float bbox1[2][3], const float bbox2[2][3], float result[2][3]) {
for (int j=0; j<3; j++) {
result[0][j] = min(bbox1[0][j], bbox2[0][j]);
result[1][j] = max(bbox1[1][j], bbox2[1][j]);
}
}
// ポリゴンリストからAABBを生成
void createAABBfromTriangles(const vector<Triangle *> &triangles, float bbox[2][3]) {
emptyAABB(bbox);
for_each(triangles.begin(), triangles.end(), [&bbox](const Triangle *t) {
mergeAABB(t->bbox, bbox, bbox);
});
}
BVH_node nodes[10000]; // ノードリスト.本当は適切なノード数を確保すべき
int used_node_count = 0; // 現在使用されているノードの数
float T_tri = 1f; // 適当
float T_aabb = 1f; // 適当
float INF = 9999999; // 適当に大きい値
// nodeIndex で指定されたノードを、polygons を含む葉ノードにする
void makeLeaf(vector<Triangle *> &polygons, BVH_node *node) {
node->children[0] = node->children[1] = -1;
node->polygons = polygons;
}
// 与えられたポリゴンリストについて、SAH に基づいて領域分割
// nodeIndex は対象ノードのインデックス
//
void constructBVH_internal (vector<Triangle *> &polygons, int nodeIndex) {
BVH_node *node = &nodes[nodeIndex];
createAABBfromTriangles(polygons, node->bbox); // 全体を囲うAABBを計算
// 領域分割をせず、polygons を含む葉ノードを構築する場合を暫定の bestCost にする
float bestCost = T_tri * polygons.size();
int bestAxis = -1; // 分割に最も良い軸 (0:x, 1:y, 2:z)
int bestSplitIndex = -1; // 最も良い分割場所
float SA_root = surfaceArea(node->bbox); // ノード全体のAABBの表面積
for (int axis=0; axis<3; axis++) {
// ポリゴンリストを、それぞれのAABBの中心座標を使い、axis でソートする
sort(polygons.begin(), polygons.end(),
[axis](const Triangle *a, const Triangle *b) {
return a->bbox.center[axis] < b->bbox.center[axis];
});
vector<Triangle *> s1, s2(polygons); // 分割された2つの領域
float s1bbox[2][3]; emptyAABB(s1bbox); // S1のAABB
// AABBの表面積リスト。s1SA[i], s2SA[i] は、
// 「S1側にi個、S2側に(polygons.size()-i)個ポリゴンがあるように分割」したときの表面積
vector<float> s1SA(polygons.size()+1, INF), s2SA(polygons.size()+1, INF);
// 可能な分割方法について、s1側の AABB の表面積を計算
for (int i=0; i<=polygons.size(); i++) {
s1SA[i] = fabs(surfaceArea(s1bbox)); // 現在のS1のAABBの表面積を計算
if (s2.size() > 0) {
// s2側で、axis について最左 (最小位置) にいるポリゴンをS1の最右 (最大位置) に移す
Triangle *p = s2.front();
s1.push_back(p); s2.pop_front();
// 移したポリゴンのAABBをマージしてS1のAABBとする
mergeAABB(s1bbox, p->bbox, s1bbox);
}
}
// 逆にS2側のAABBの表面積を計算しつつ、SAH を計算
float s2bbox[2][3]; emptyAABB(s2bbox);
for (int i=polygons.size(); i>=0; i--) {
s2SA[i] = fabs(surfaceArea(s2bbox)); // 現在のS2のAABBの表面積を計算
if (s1.size() > 0 && s2.size() > 0) {
// SAH-based cost の計算
float cost =
2*T_aabb + (s1SA[i]*s1.size() + s2SA[i]*s2.size()) * T_tri / SA_root;
// 最良コストが更新されたか?
if (cost < bestCost) {
bestCost = cost; bestAxis = axis; bestSplitIndex = i;
}
}
if (s1.size() > 0) {
// S1側で、axis について最右にいるポリゴンをS2の最左に移す
Triangle *p = s1.back();
s2.insert(0, p); s1.pop_back();
// 移したポリゴンのAABBをマージしてS2のAABBとする
mergeAABB(s2bbox, p->bbox, s2bbox);
}
}
}
if (bestAxis == -1) {
// 現在のノードを葉ノードとするのが最も効率が良い結果になった
// => 葉ノードの作成
makeLeaf(polygons, node);
} else {
// bestAxis に基づき、左右に分割
// bestAxis でソート
sort(polygons.begin(), polygons.end(),
[bestAxis](const Triangle *a, const Triangle *b) {
return a->bbox.center[bestAxis] < b->bbox.center[bestAxis];
});
// 左右の子ノードを作成
used_node_count++;
node->children[0] = used_node_count;
used_node_count++
node->children[1] = used_node_count;
// ポリゴンリストを分割
vector<Triangle *> left(polygons.begin(), polygons.begin()+bestSplitIndex);
vector<Triangle *> right(polygons.begin()+bestSplitIndex, polygons.end());
// 再帰処理
constructBVH_internal (left, node->children[0]);
constructBVH_internal (right, node->children[1]);
}
}
// フロントエンド関数.これを呼べば nodes[0] をルートとした BVH が構築される
void constructBVH(vector<Triangle *> &polygons) {
used_node_count = 0;
constructBVH_internal(polygons, 0); // nodes[0] をルートノードとみなす
}
※このコードは、(Ingo and et al., 2007) の疑似コードを参考に書いています
constructBVH 関数に読み込んだモデルの三角形のリストを渡せば、nodes[0] をルートノードとした BVH が構築されます。
BVH_node 構造体
この構造体が、BVH の各ノードを表します
中身には、ノードが保持する AABB と、2つの子ノードのインデックスです。
葉ノードの場合、子ノードが存在しないのでこのインデックスは -1 になります。
BVH は完全二分木になるので、children[0] != -1, children[1] == -1 のようなことにはなりません。
AABB の表現が float bbox[2][3] という形になっています。図で表すとこんな感じです。
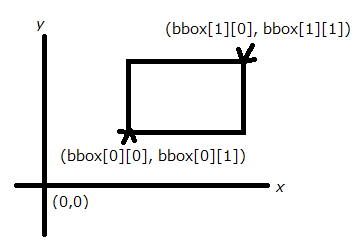
bbox[0] が AABB の最小座標、bbox[1] が最大座標を示しています。
配列の2次元目はxyz座標を示しています(0がx, 1がy, 2がz)。
最後に、polygons というメンバがありますが、これはノードが葉ノードの時のみ有効で、格納しているポリゴンのリストを示します。
このデータ構造は明らかに効率が悪いのは見た瞬間わかると思います。
polygons メンバは葉ノードでしか有効でなく、中間ノードでは無駄にメモリを食ってしまうだけになります。
これをどうにかするには、例えば整列済みの vector をどこかに1つ保持しておき、葉ノードはこの配列のどこからどこまでを自分が持つポリゴンなのか、という情報を保持する方法があります。
この場合、以下のようなデータ構造になります。
struct BVH_node {
float bbox[2][3];
// ノードが葉の場合、children[0]の先頭ビットが1となる。また、下位31ビットはそれぞれ以下の値になる
// children[0]: ポリゴンリストの先頭インデックス children[1]: 保持するポリゴンの数
int children[2];
};
...
if (0x80000000 & node->children[0]) {
// 葉ノード
int index = 0x80000000 ^ node->children[0];
int count = node->children[1];
}
children メンバ中の1ビットだけを使って葉ノード判定を行い、インデックスやポリゴン数は 残りの 31+32 ビットを使って表します。
このほうが効率はいいのですが、ここではわかりやすさのために vector<Triangle *> polygons というメンバでコードを示しています。
各種ユーティリティ関数
surfaceArea は与えられた AABB の表面積を求めます。
emptyAABB は与えられた AABB を空のAABBとして初期化します。
空のAABBとは何ぞや、といったところですが、要素を全部0で初期化してしまうと、後述する mergeAABB がうまく動かなくなるので、最小座標に INF を入れ、最大座標に -INF を入れることで無効なAABBを空のAABBとここではしています。
mergeAABB は与えられた2つのAABBを1つのAABBに合体させます。
各軸について最小座標と最大座標が分かれば AABB になるので、2つを比較して min と max をとるだけです。
createAABBfromTriangles は、与えられたポリゴンリストを内包するAABBを求めます。
ここで、各ポリゴンは AABB をそれぞれ所持しているということにしているので、それらをすべて merge することで実現しています。
makeLeaf は与えられたノードを、同じく与えられたポリゴンリストを保持する葉ノードとして設定します。
前述したとおり、children に -1 を設定し、保持するポリゴンリストを設定しています。
以上のユーティリティ関数を使いながら、実際の分割処理である constructBVH_internal が実行されます。
constructBVH_internal (実際の分割処理)
まず最初に、前述した createAABBfromTriangles を用い、与えられたポリゴンをすべて含む AABB を計算してノードに設定しています。
BVH_node *node = &nodes[nodeIndex];
createAABBfromTriangles(polygons, node->bbox); // 全体を囲うAABBを計算
続いて、最も低コストな領域分割を探索するための変数の初期化です。
// 領域分割をせず、polygons を含む葉ノードを構築する場合を暫定の bestCost にする
float bestCost = T_tri * polygons.size();
int bestAxis = -1; // 分割に最も良い軸 (0:x, 1:y, 2:z)
int bestSplitIndex = -1; // 最も良い分割場所
float SA_root = surfaceArea(node->bbox); // ノード全体のAABBの表面積
bestCost は、このノードを葉ノードとしてしまう場合のコストを初期値としています。
これにより、さらに分割を行うべきか、葉ノードとしてしまうのがいいのか、を判定できます。
bestAxis, bestSplitIndex は探索結果を格納する変数で、SA_root は先ほど計算したAABBの表面積です。
続いて axis についての for 文が入ります。
この for 文で、「x座標で分割」「y座標で分割」「z座標で分割」の3種類についてそれぞれコストを調べます。
その直後に、polygons を axis に基づいてソートします。
sort(polygons.begin(), polygons.end(),
[axis](const Triangle *a, const Triangle *b) {
return a->bbox.center[axis] < b->bbox.center[axis];
});
可能な分割の組み合わせを全て試すのはものすごい時間がかかる&分割された2つの領域はできるだけ重ならないほうが効率が良い、ということから、「AABB の中心座標でソートし、その配列を2つに分ける」という方法で分割を行います。
次に、ソートされた配列の区切り場所ごとで、2つの領域の表面積がどうなるかを計算します (s1SA, s2SA)。
例えば以下のように7つのポリゴンが polygons にあり、△をS1に、▲をS2に分割する場合、S1のAABBの表面積はs1SA[4]に、S2の表面積はs2SA[4]に格納されます。
polygons: △△△△▲▲▲
計算処理自体はそこまで複雑なことをやってないです。
i=0 の時 (S1空で全部S2に入る) を起点とし、最初のループでは s1SA を計算しています。
この時「何故同時にs2SAも計算しないのか?」と思われるかもしれません。
これは、S1はiの増加に合わせてポリゴンが増えるので、そのAABBはmergeAABBで計算できるが、「S2はiの増加に合わせてポリゴンが減るので、その都度 createAABBfromTriangles をしないと AABB が計算できず、処理が重くなる」という問題点があるからです。
そのため、2つ目のループで s2SA の計算をしています。
s2SA の計算では、i=polygons.size() (全部S1に入ってS2空) の状態から i=0 の状態に向かってループを回しています。
既に s1SA は計算済みなので、SAH-based なコストを計算することが出来ます。
float cost = 2*T_aabb + (s1SA[i]*s1.size() + s2SA[i]*s2.size()) * T_tri / SA_root;
前述した数式通りの式になってます。
このコストを最小化したいので、暫定的な最良コストを下回った場合、各種データを更新します。
以上の、axis についての for の中身が終了すると、bestAxis や bestSplitIndex に最も良い分割についての情報が入っています。
bestAxis が -1 だった場合、つまり一度も bestCost の更新が行われなかったので、「葉ノードとするのが最も低コスト」であるので、makeLeaf を呼び出して終了しています。
そうでなかった場合、ポリゴンリストを分割して再帰呼び出しを行う必要があります。
bestAxis について再度ソートをした後、以下のような処理が行われます。
// 左右の子ノードを作成
node->children[0] = used_node_count; used_node_count++;
node->children[1] = used_node_count; used_node_count++;
// ポリゴンリストを分割
vector<Triangle *> left(polygons.begin(), polygons.begin()+bestSplitIndex);
vector<Triangle *> right(polygons.begin()+bestSplitIndex, polygons.end());
// 再帰処理
constructBVH_internal (left, node->children[0]);
constructBVH_internal (right, node->children[1]);
まず最初に、子ノードの領域を確保します。
nodes[0~used_node_count-1] は使用済みなので、その後ろ2つを新しい子ノードの領域としています。
次に、bestSplitIndex に基づいて分割された2つのポリゴンリストを作ります。
bestSplitIndex は、S1 側に polygons[0, bestSplitIndex) を、S2側に polygons[bestSplitIndex, size-1] を割り当てる、といったことを表しています。
これをvectorで実装すると上記コードの真ん中のようになります(もっといい書き方あるだろうけど)。
そして最後に、分割された2つの領域それぞれについて、再帰を行うことでさらに分割を行っていきます。
constructBVH
constructBVH_internal へのフロントエンド関数です。
used_node_count = 0; で全てのノードを未使用状態にし、ルートノードのインデックスである 0 を引数として constructBVH_internal を呼び出しています。
以上が SAH-based の BVH の構築方法になります。
コストの計算式自体はそんなに難しいことはないですが、AABB を扱うための種々の関数等を入れるとちょっとコードが長くなってしまいました。
もちろんこのコードはかなり適当に書いているので、実用するうえでは、class にまとめたりエラーチェックをしたり確保するノードの数に気を遣ったりしてください。
構築例
Stanford Bunny で実際に分割してみた例です。

Bunny のモデルと、AABB のワイヤーフレームを表示しています。
左上→右上→左下→右下 と進むごとに、BVH の木の深い階層のAABBを表示しています。左上はルートノードの AABB になります。
これを見ると、なんとなくそれっぽいかな?という分割結果が得られています。
耳の部分と顔の部分が分かれている部分などが特にそれっぽい感じになっていると思います。
この結果を用いて、実際にレイトレを行う時のレイとモデルの交差判定を行います。
BVH によるレイの交差判定処理
長くなってしまったので、これについては記事を分けたいと思います…
記事書きました → Bounding Volume Hierarchy (BVH) の実装 - 交差判定編
参考文献
Ingo Wald, Solomon Boulos, and Peter Shirley, Ray Tracing Deformable Scenes using Dynamic Bounding Volume Hierarchies, ACM Transactions on Graphics 26(1), 2007.
林 秀一, 実践!QBVH, http://www.slideshare.net/ssuser2848d3/qbv