この記事はレイトレ合宿2アドベントカレンダーの五週目の記事です。
そして Bounding Volume Hierarchy (BVH) の実装 - 構築編 の続きにもなります。
構築編を書いたのが去年の12月なので、ゆうに半年以上経ってようやく記事が完成する形に…
構築編の続きとなるので、構築編を読んでおられない方は構築編からどうぞ。
BVH を使わない場合の交差判定
早速タイトルと違うことを言っていますが、まずは全てのポリゴンに総当たりしてチェックする方法を確認しておきましょう。
これに関してはコードを示してしまったほうがおそらくわかりやすいです。
int Intersect(const Vector<Triangle *> &polygons, const Ray ray) {
for (int i=0; i<polygons.size(); i++) {
Triangle *polygon = polygons[i];
if (polygon->Intersect(ray)) {
return i;
}
}
return -1;
}
たったこれだけです。全てのポリゴンに対して、レイが当たっているかどうかをチェックするだけです。
(ポリゴンとレイの交差判定に関しては、レイトレ合宿2アドベントカレンダー1週目の、レイとの交差判定 等を参照してください。
ここで紹介されている、[Möller–Trumbore intersection algorithm] (http://en.wikipedia.org/wiki/M%C3%B6ller%E2%80%93Trumbore_intersection_algorithm) がシンプルかつ高速で良いです。
http://shikousakugo.wordpress.com/2012/07/01/ray-intersection-3/ なども参考にしました)
こんなにシンプルになるのですが、これは滅茶苦茶重いです。
特に、「レイが、ポリゴンが構成しているモデルとは明後日の方向を向いている」場合にも全てチェックしないといけないので、ムダ極まりないです。
BVH を使えば、そのような場合でもレイとAABB1回の交差判定だけで済みます。
というわけで、前置きは終わりにして BVH を用いた交差判定に入ります。
BVH を使った交差判定
BVH を使った交差判定は以下のような流れになります。
BVH_node の構造は、構築編で用いたものと同じものを使います。
struct IntersectInformation {
float normal[3];
float distance;
};
Triangle * Intersect(BVH_node *nodes, int index, const Ray &ray, IntersectInformation &info) {
チェック対象ノード = nodes[index];
if (チェック対象ノードのAABBとrayの交差判定) {
// 交差している
if (対象ノードは中間ノード?) {
// 中間ノードなので、さらに子を調べる
int result1 = Intersect(nodes, 子ノード1, ray, info);
int result2 = Intersect(nodes, 子ノード2, ray, info);
return result1 と result2 のうち、ray の始点に近い方;
} else {
return ノードに含まれるすべてのPolygonとrayの交差判定結果 (詳細は o_info に入れる);
}
} else {
// 交差していない
// → 現在のノードの子ノードは、全て現在のノードのAABBに内包されるので、ここで探索を打ち切って良い
return -1;
}
}
...
// intersectId にレイが交差したオブジェクトのIdが入っている
int intresectId = Intersect(rootNode, 0, ray);
IntersectInformation は、交差判定の詳細結果を保持します。
具体的には、交差したポリゴンの法線と、レイから交差した地点までの距離を示します。
この交差判定のポイントは4つです
- BVH の各ノードの AABB と ray の交差判定を行う
- 中間ノードの場合、さらに子について再帰的に交差判定を行う
- 末端ノードの場合、ノードが含むすべてのポリゴンについて交差判定を行う
- AABB と ray が交差していなかった場合、そこで探索をやめ、「交差していない」という結果を返す
何故この流れで判定できるのか、ということも含めてそれぞれについて説明をしていきます。
AABB と ray の交差判定
まずはじめに、AABB と ray の交差判定を行います!が、ここでそれを一から説明してるとすごい長くなってしまうので、原理は省略…
ゲームつくろー! - その18 直線とAABB などが図付で説明が分かりやすいです。
上記のサイトでは、2次元平面上での交差判定を図のレイとして挙げていますが、3次元空間上でもやり方は同じです。
コードにするとこんな感じ。
AABB の表現方法は、構築編と同じ方法を見ているので、よくわからなければそちらを見てください。
struct Ray {
float org[3]; // レイの始点
float dir[3]; // レイの方向ベクトル (正規化済み)
};
bool IntersectAABBvsRay(float aabb[2][3], const Ray &ray) {
// aabb[0][0], aabb[0][1], aabb[0][2]: AABB の最小座標のx,y,z
// aabb[1][0], aabb[1][1], aabb[1][2]: AABB の最大座標のx,y,z
float t_max = FLT_MAX // AABB からレイが外に出る時刻
float t_min = -FLT_MAX; // AABB にレイが侵入する時刻
for (int i=0; i<3; i++) {
float t1 = (aabb[0][i] - ray.org[i])/ray.dir[i];
float t2 = (aabb[1][i] - ray.org[i])/ray.dir[i];
float t_near = std::min(t1, t2);
float t_far = std::max(t1, t2);
t_max = std::min(t_max, t_far);
t_min = std::max(t_min, t_near);
// レイが外に出る時刻と侵入する時刻が逆転している => 交差していない
if (t_min > t_max) return false;
}
return true;
};
これで AABB とレイの交差判定が出来ます。
一つ注意すべき点は、ray.dir[i] で割り算をしているところです。
例えば y-z 平面にレイが平行だった場合、ray.dir[0] は 0 になるため、0除算が発生してしまいます。
また、完璧に0じゃなくても、ものすごく値が小さくなる場合もあります。
この問題への簡単な対処法は、ray.dir[i]があまりに小さい場合、平面に平行だとみなして、
aabb[0][i] <= ray.org[i] <= aabb[1][i] なら t_near = -FLT_MAX, t_max = FLT_MAX とし、
この条件を満たさないならこの軸に関しては当たっていない、とみなす方法です。
ただし、それを判別する閾値次第ではそれでも誤判定してしまう場合があるため、完璧な方法ではありません。
子ノードの交差判定
もしノードのAABBとレイが交差していた場合、かつノードが葉ノードではなく中間ノードだった場合、次はその子ノードの判定です。
これは再帰的に Intersect 関数を呼び出すだけです。
// BVH_node 再掲
struct BVH_node {
float bbox[2][3]; // bbox[0,1]: AABB の最小,最大座標. bbox[hoge][0,1,2]: x,y,z座標
int children[2]; // 子ノード
vector<Triangle *> polygons; // 格納されているポリゴン (葉ノードのみ有効)
};
...
if (IntersectAABBvsRay(nodes[index].bbox, ray)) {
// 中間ノードか?
if (nodes[index].children[0] != -1) {
Triangle *childResult = -1;
// 両方の子ノードについて調べる
for (int i=0; i<2; i++) {
Triangle *result = Intersect(nodes, nodes[index].children[0], polygons, ray, info);
if (result != nullptr) {
childResult = result;
}
}
if (childResult != nullptr) return childResult;
}
}
...
こんな感じです。
このコードだけ見ると、「children[0], children[1] 両方で交差していた場合どうするの??」と思われる方もいるでしょう。
後だしじゃんけんのようになりますが、この Intersect 関数は 「info に入っている distance より、近い位置でポリゴンとの交差を検知した場合のみ、交差したとみなす」 となるように作ります。
こうしておけば、子の両方でレイが交差していた場合も、より近いほうだけが結果として反映されます。
末端ノードのポリゴンの交差判定
続いて、AABB とレイが交差していて、かつ「ノードが葉ノード」だった場合です。
葉ノードの場合、ノードにポリゴンのリストが入っています。
ここでは、単純にすべてのポリゴンについて総当たりでチェックを行います。
...
if (IntersectAABBvsRay(nodes[index]->bbox, ray)) {
// 中間ノードか?
if (nodes[index].children[0] != -1) {
// 中間ノード
...
} else {
// 葉ノード
Triangle *result = nullptr;
for (Triangle *tri : nodes[index].polygons) {
// ポリゴンとレイの交差判定
// distance に交差していた場合のレイからの距離、normal にポリゴンの法線が入る
float distance = 0.f;
float normal[3];
if (tri->Intersect(ray, distance, normal)) {
// 既に交差したと判定された他のポリゴンより、レイの始点に近いかどうか
if (distance < info.distance) {
result = tri;
info.distance = distance;
for (int i=0; i<3; i++) info.normal[i] = normal[i];
}
}
}
if (result != nullptr) return result;
}
}
...
ノードが含む全てのポリゴンについて Triangle::Intersect を行い、その結果、レイと交差しており、かつ
「現時点で、レイの始点に最も近い場所で交差している、とみなされているポリゴンより近くで交差した」
場合のみ結果を反映するようにしています。
肝心の Triangle::Intersectですが、最初の総当たり法でも述べたように、ここで説明すると長くなるので詳細は割愛します。
AABB と ray が交差していなかった場合
最後に、AABBとレイが交差していなかった場合です。
これは非常に単純です。BVH の各ノードは、必ず子ノードに存在する全てのポリゴンを内包します。
そのため、レイがAABBと交差していなかった場合、そこに含まれるすべてのポリゴンとも交差していない、ということになります。
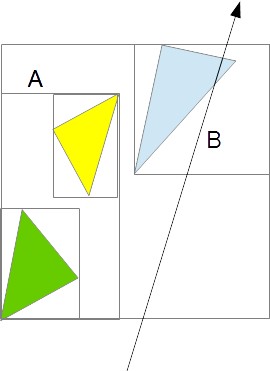
例えば以下のような場合です。
レイは「A」には交差していないため、それが内包する黄色と緑のポリゴンとは交差しようがありません。
このため、AABBとレイが交差していなかった場合、何もせずに「交差していない」という情報を返すだけになります。
まとめ
以上で構築した BVH での、ポリゴンとレイとの交差判定が出来るようになります。
最後に、それぞれの項目でばらばらに書いたコードをここにまとめて書きます。
// レイ
struct Ray {
float org[3]; // レイの始点
float dir[3]; // レイの方向ベクトル (正規化済み)
};
// 交差判定情報
struct IntersectInformation {
float normal[3];
float distance;
};
// BVH_node 再掲
struct BVH_node {
float bbox[2][3]; // bbox[0,1]: AABB の最小,最大座標. bbox[hoge][0,1,2]: x,y,z座標
int children[2]; // 子ノード
vector<Triangle *> polygons; // 格納されているポリゴン (葉ノードのみ有効)
};
bool IntersectAABBvsRay(float aabb[2][3], const Ray &ray);
Triangle * Intersect(BVH_node *nodes, int index, const Ray &ray, IntersectInformation &info) {
// AABB とレイの交差判定
if (IntersectAABBvsRay(nodes[index].bbox, ray)) {
// 交差している
// 中間ノードか?
if (nodes[index].children[0] != -1) {
// 中間ノード
// 両方の子ノードについて調べる
Triangle *childResult = -1;
for (int i=0; i<2; i++) {
Triangle *result = Intersect(nodes, nodes[index].children[0], polygons, ray, info);
if (result != nullptr) {
childResult = result;
}
}
if (childResult != nullptr) return childResult;
} else {
// 葉ノード
Triangle *result = nullptr;
for (Triangle *tri : nodes[index].polygons) {
// ポリゴンとレイの交差判定
// distance に交差していた場合のレイからの距離、normal にポリゴンの法線が入る
float distance = 0.f;
float normal[3];
if (tri->Intersect(ray, distance, normal)) {
// 既に交差したと判定された他のポリゴンより、レイの始点に近いかどうか
if (distance < info.distance) {
result = tri;
info.distance = distance;
for (int i=0; i<3; i++) info.normal[i] = normal[i];
}
}
}
if (result != nullptr) return result;
}
} else {
// 交差していない (何もする必要なし)
}
return nullptr;
}
bool IntersectAABBvsRay(float aabb[2][3], const Ray &ray) {
// aabb[0][0], aabb[0][1], aabb[0][2]: AABB の最小座標のx,y,z
// aabb[1][0], aabb[1][1], aabb[1][2]: AABB の最大座標のx,y,z
float t_max = FLT_MAX // AABB からレイが外に出る時刻
float t_min = -FLT_MAX; // AABB にレイが侵入する時刻
for (int i=0; i<3; i++) {
float t1 = (aabb[0][i] - ray.org[i])/ray.dir[i];
float t2 = (aabb[1][i] - ray.org[i])/ray.dir[i];
float t_near = std::min(t1, t2);
float t_far = std::max(t1, t2);
t_max = std::min(t_max, t_far);
t_min = std::max(t_min, t_near);
// レイが外に出る時刻と侵入する時刻が逆転している => 交差していない
if (t_min > t_max) return false;
}
return true;
};
...
// Intersect 呼び出し
IntersectInformation hitInfo;
hitInfo.distance = FLT_MAX;
Triangle *hitTriangle = Intersect(bvhRoot, 0, ray, hitInfo);
以上のようになります。
それぞれ別々に書いてたコードをくっつけただけなので、特に説明はありません。
BVH あり/なしの比較
BVH を使った場合、使わなかった場合の比較です。
コーネルボックスに、970個のポリゴンで構成されたオブジェクトを置いて、4並列で10分間レンダリングした結果です。
まるで結果が違いますね。
このようなシーンの場合、レイがモデルに当たる場合より、当たらない場合のほうがはるかに多くなります。
そのような場合、BVHを使えば1回のAABBとの交差判定で済みますが、BVH無しで総当たりで判定する場合、そのような場合でも逐一すべてのポリゴンに対して交差判定をする必要があります。
そのため、ここまで差が出てくる結果となります。
ちなみに、BVH をさらに発展させたものに、QBVH というものもあります。
名前から分かる通り、1つのノードが4つの子ノード (Quater) を持つ構造です。
もっと高速化したい!という方は、実践!QBVH 等を読んでみるといいと思います(大本の論文を読めるのであれば論文を読むのが一番です)。
参考文献
Ingo Wald, Solomon Boulos, and Peter Shirley, Ray Tracing Deformable Scenes using Dynamic Bounding Volume Hierarchies, ACM Transactions on Graphics 26(1), 2007.
H. Dammertz1 and J. Hanika1 and A. Keller, Shallow Bounding Volume Hierarchies for Fast SIMD Ray Tracing of Incoherent Rays, http://www.uni-ulm.de/fileadmin/website_uni_ulm/iui.inst.100/institut/Papers/QBVH.pdf
林 秀一, 実践!QBVH, http://www.slideshare.net/ssuser2848d3/qbv
q, レイとの交差判定, http://qpp.bitbucket.org/post/collection_of_intersection/
よしむ, 試行錯誤 - Ray Intersection #3, http://shikousakugo.wordpress.com/2012/07/01/ray-intersection-3/
IKD, 〇×つくろーどっとコム - その18 直線とAABB, http://marupeke296.com/COL_3D_No18_LineAndAABB.html