追記: U-Netの中間層は常にSelf-Attentionとなります。ご指摘いただきました。ありがとうございます。（コード）

オミータです。ツイッターで人工知能のことや他媒体の記事など を紹介しています。 @omiita_atiimoもご覧ください！

世界に衝撃を与えた画像生成AI「Stable Diffusion」を徹底解説！

未来都市にたたずむサンタクロース（Stable Diffusionで生成）

2022年8月、世界に大きな衝撃が走りました。それは、Stable Diffusionの公開です。Stable Diffusionは、テキストを受け取るとそれに沿った画像を出力してくれるモデルです¹。Stable Diffsuionは10億個近いパラメータ数をもち、およそ20億個の画像とテキストのペア（LAION-2B）で学習されています。これにより、Stable Diffusionは入力するテキスト（呪文とも呼ばれています。）を工夫することで、複雑な画像でもいとも簡単に生成してしまいます。Stable Diffusionの前にもMidjourneyやDALL-E 2など、入力テキストを画像に変換してくれるモデルは存在していました。そんな中、Stable Diffusionがひときわ注目されたのは、「Stable Diffusionがだれでも無制限に使えたこと」が非常に大きいです。それまでの高精度なテキスト画像変換モデルはAPIの公開（そして有料）などに限られていました。その一方で、Stable Diffusionはコードに加え学習済みの重みも公開されました。

本記事では、そんなStable Diffusionの中身が何で構成されているのかを図を交えながら見ていきます。仕組みを知ることでどのように応用することができるかがわかってきます。その中からStable Diffusionの思わぬ使い方が見えてくるかもしれません。それではStable Diffusionの中身の説明へと入りましょう！

本記事では、「Stable Diffsuion」と、その元の論文での呼び名である「Latent Diffusion Model（LDM）」という言葉が出てきます。本記事においては、それらは同じものを指しています。

本記事の流れ:

• 忙しい方へ
• Stable Diffusion
• 拡散モデル
• VAE
• U-Net
• Stable Diffusionを動かす
• まとめと所感
• 参考

原論文: "High-Resolution Image Synthesis with Latent Diffusion Models", Rombach, R., Blattmann, A., Lorenz, D., Esser, P., Ommer, B. (CVPR'22)

0. 忙しい方へ

Stable Diffusionの全体像

• Stable Diffusionは、おおきく以下の3つで構成されるよ
  1. 拡散モデル（U-Net）
  2. VAE
  3. Text Encoder（Transformer）
• Stable Diffusionは、VAEの潜在空間に対して拡散モデルを学習させることで、効率よく高解像度の画像生成ができるよ
• Text EncoderはCLIPで学習されているよ
• テキストによる条件付けは、U-Net内のCross-Attentionでおこなっているよ

1. Stable Diffusionとは

Stable Diffusionはテキストを画像に変換するモデル

Stable Diffusionとは、テキストを入力するとそれに沿った画像を生成してくれるモデルです。まずは、その中身をざっくりと見ていきます。

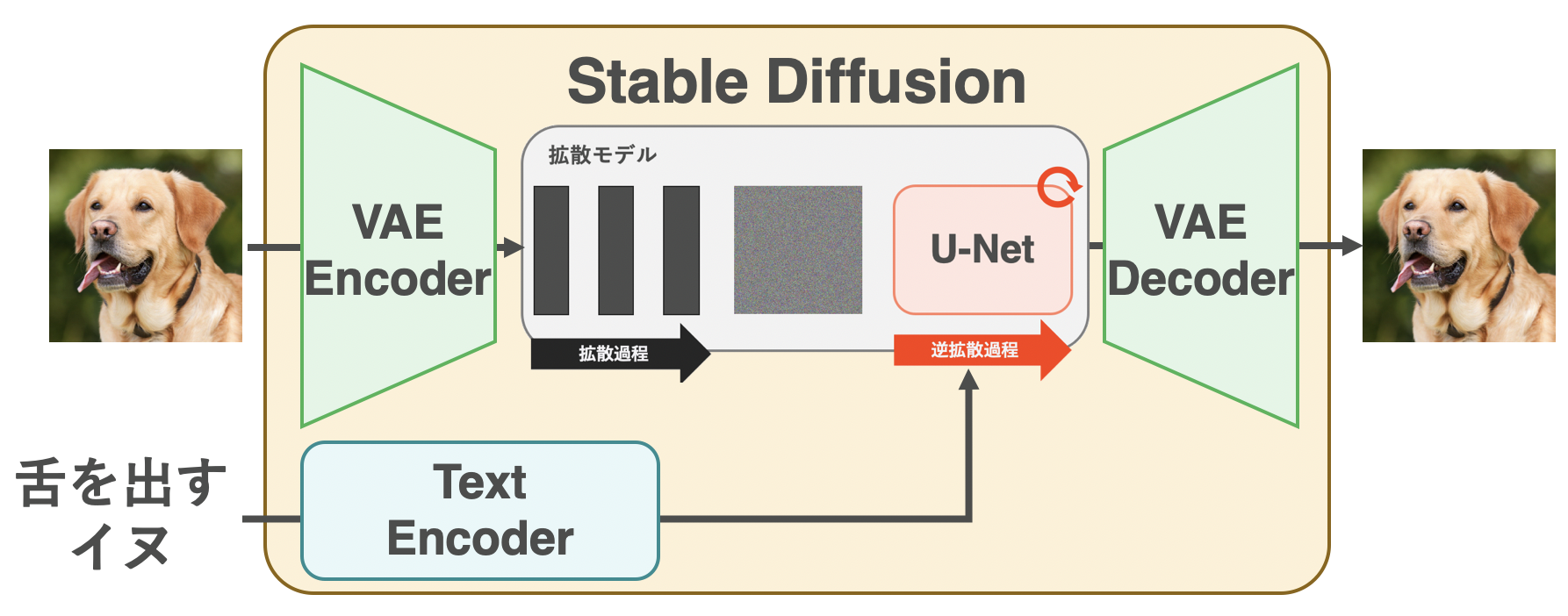
Stable Diffusionの全体像

Stable Diffusionの中身は上図²のように大きく3つのパーツで構成されています。

1. 拡散モデル（U-Net）
2. VAE
3. Text Encoder（Transformer）

拡散モデルを中心におき、その両端をVAEのエンコーダとデコーダによって挟んでいるようなアーキテクチャになっています。入力テキストは、Text Encoderを通ってベクトルに変換され、拡散モデルの横から組み込まれます。

本記事のこの後の流れですが、まずは、拡散モデルについて見ていきます。その後、拡散モデルがはらんでいる問題点をVAEを用いることで解消できることを説明します。そして最後に、Stable Diffusionで一番大切な拡散モデルを構成するU-Netのアーキテクチャを見ていきます。その際に、テキストがText Encoderによってどのように処理されていくかを見ていきます。

2. 拡散モデル

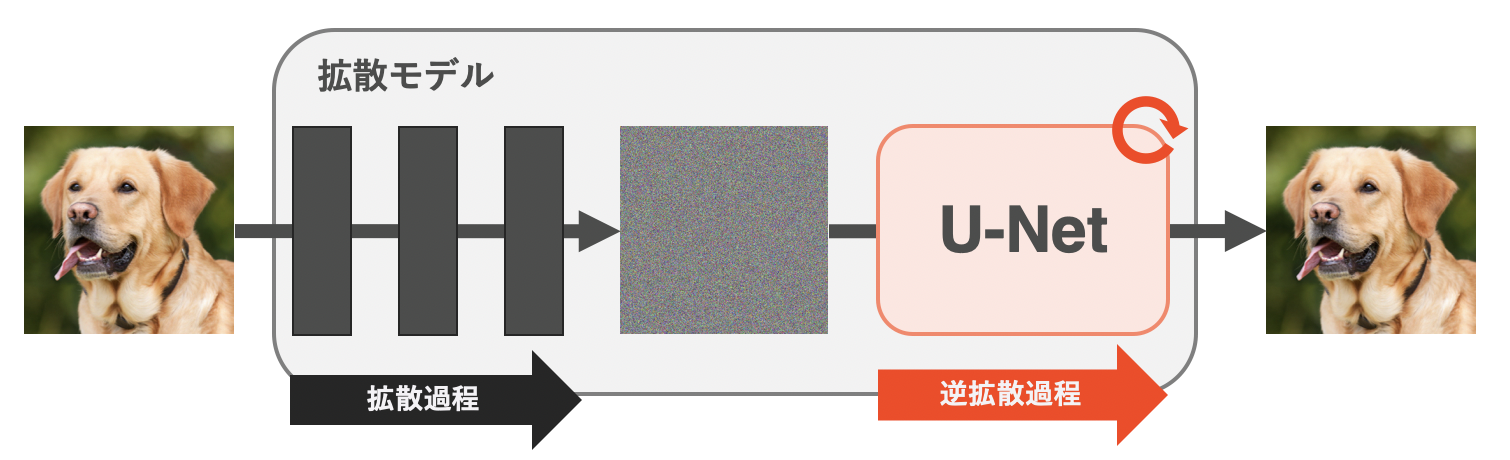
拡散モデルの全体像

拡散モデルとは、「ノイズ画像から少しずつノイズを取り除くことでキレイな画像を生成」するモデルです。上の図は拡散モデルの概略図を示しており、以下の2つのプロセスから成り立っています。

1. 拡散過程（= 順過程）
2. 逆拡散過程（= 逆過程）

拡散過程とは、キレイな画像（上図左の犬）にノイズを少しずつ加えて、最終的に完全なノイズ画像（上図の真ん中）にするプロセスのことです。一方、逆拡散過程とは、その逆なので、完全なノイズ画像から少しずつノイズを取り除くことで、最終的にキレイな画像（上図右の犬）を生成するプロセスです。先に言っておくと、拡散過程にはガウシアンノイズ、逆拡散過程にはU-Netを用います。それでは、それぞれについてもう少し詳しく見ていきましょう。

2.1 拡散過程

拡散過程の全体像

拡散過程とは、キレイな画像に少しずつノイズを加えていく過程のことです。上図は、図左の犬の画像に対する拡散過程を表しています。拡散過程を経て最終的に図の一番右のような完全なノイズ画像になっていることがわかります。

拡散過程の１ステップ

上の図はノイズを加える1ステップを切り出したものです。ノイズを加える各ステップは時刻と呼ばれ、$t$で表します。そして各時刻で加えるノイズ$\mathbf{\epsilon}_t$はガウシアンノイズです。図左のキレイな画像に対する時刻を$t=0$とし、最終的な時刻を$T$とします。上図は、$T=3$の例です。この$T$の値はハイパーパラメータであり、拡散モデルが注目されるきっかけとなったDDPM（Denoising Diffusion Probabilistic Model）[Ho, J. (NeurIPS'20)]やStable Diffusionの元となっているLDM（Latent Diffusion Model）[Rombach, R.(CVPR'22)]では$T=1000$が用いられています。つまり、微量のガウシアンノイズを1,000回加算しつづけるということです。

[Nichol, A. (ICML'21)]図3を一部改変。線形ノイズスケジューラとコサインノイズスケジューラの比較。

ただ、1,000回加算し続けると言っても各時刻でどのくらいの量のノイズを加えるのが良いのでしょうか。これは、ノイズスケジューラによって決定します。 各時刻で加えるノイズの値をノイズスケジューラによって変動させていくのです。上図は、「線形スケジューラ」と「コサインスケジューラ」によってノイズを加算した例です。左が時刻$t=0$で右が$t=T$です。線形スケジューラは、加えるノイズの量を時刻が進むにつれて線形に増やしていくノイズスケジューラです。DDPMやLDMはこの線形スケジューラを採用しています。

ただ、上の図を見ると分かりますが、線形スケジューラは割と早い時刻で画像がノイズだらけになってしまっています。これでは後半の画像はただのノイズばかりになってしまい、あまり意味がありません。そのため、DDPMを改良させたImproved DDPM[Nichol, A. (ICML'21)]では、コサインスケジューラを採用しています。ちなみに生成時には、学習時とは異なるノイズスケジューラ（時刻を間引くRespacingやDDIMスケジューラ）を用いることで生成のスピードを上げたりしています。

このようにノイズスケジューラの選択には自由度があることがわかりました。これで拡散過程の説明は終わりです。つづいて、加えたノイズを少しずつ取り除いていく逆拡散過程について見ていきましょう。

2.2 逆拡散過程

逆拡散過程の全体像

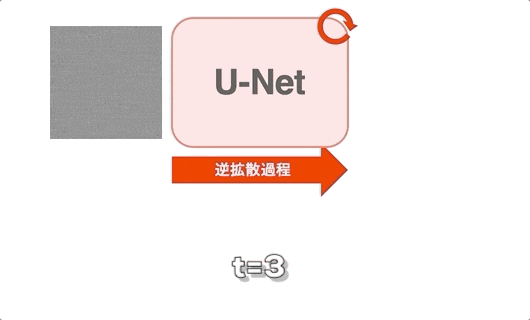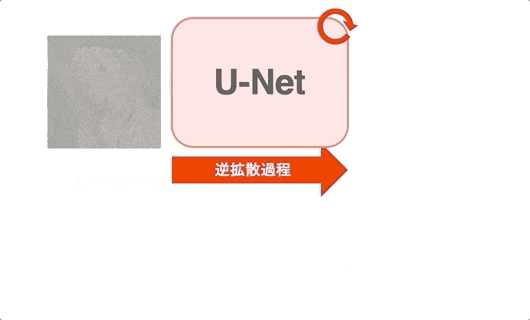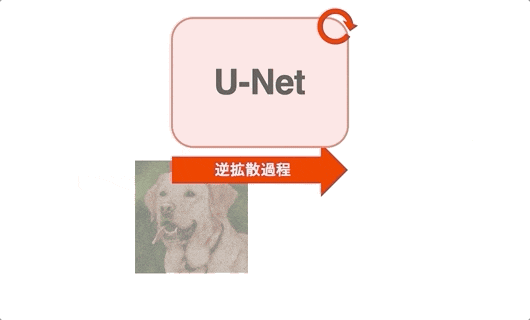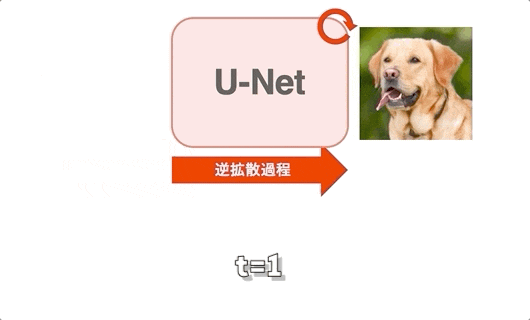
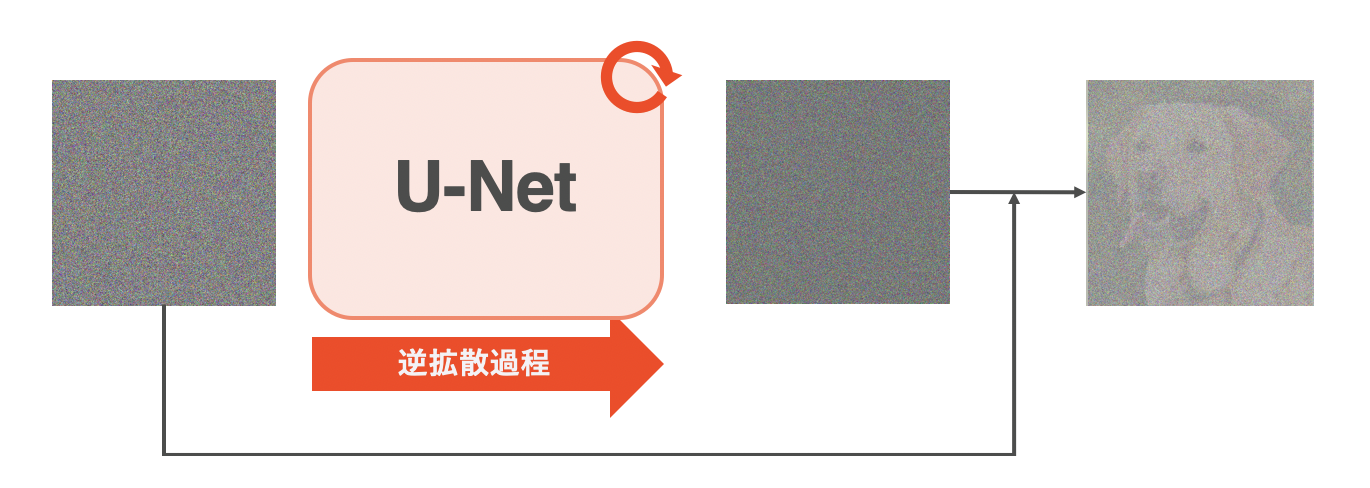
逆拡散過程は、拡散過程で加えたノイズを少しずつ取り除いていく過程のことです。上の図は、図右のノイズから図左のキレイな画像への逆拡散過程を表しています。まず拡散過程はノイズを加えるだけなので簡単に処理ができます。一方で逆拡散過程の「ノイズを取り除く」というのは自力で処理しようとしたら非常に難しいです。そこで登場するのが、ニューラルネットワークです。自力でノイズを取り除くのが難しいので、この処理をニューラルネットワークに任せてしまいます。拡散モデルでは、ニューラルネットワークとしてU-Netを用いることが多いです。Stable Diffusionも例に漏れず、U-Netを用いています。このU-Netの役割は時刻$t$の画像$\mathbf{x}_t$を、時刻$t-1$の少しだけキレイな画像$\mathbf{x}_t$に変換することです。上図からだとU-Netが各時刻に別々で存在するように思えますが、実際は全ての時刻をたった1つのU-Netが担います。つまり、上図の逆拡散過程は下の動画（gif）であらわすことができます。ここでは、便宜上左から入力、右から出力を出すようにします。また、先にネタバレをすると、下のアニメーションはわざと間違えています。詳しくは次の2.3節で説明しますが、U-Netの出力は画像ではなくノイズになります。

逆拡散過程の全体像（アニメーション）

上のgifのように、U-Netは各時刻で入力画像を少しずつキレイにしていきます。全時刻で1つのU-Netを使っているため、U-Netに「この画像は時刻が〇〇の画像ですよ！」という時刻$t$の情報を別で与えてあげる必要があります。Stable Diffusionでは、時刻$t$を位置エンコーディング（Transformerなどに用いられる正弦波のやつ）で表現します。時刻$t$をU-Netに与える方法は「U-Netのアーキテクチャ」で詳しく説明します。ここでは、U-Netの入力は「時刻$t$の画像」と「時刻$t$」であることを理解していれば大丈夫です。それではU-Netの学習方法と画像の生成方法を見ていきましょう。

2.3 U-Netの学習

U-Netの学習についてです。まずは、U-Netのターゲットを何にして、損失関数をどれにするか、ということについて説明します。そのあとに、U-Netの学習の流れを簡単にコードで見ます。

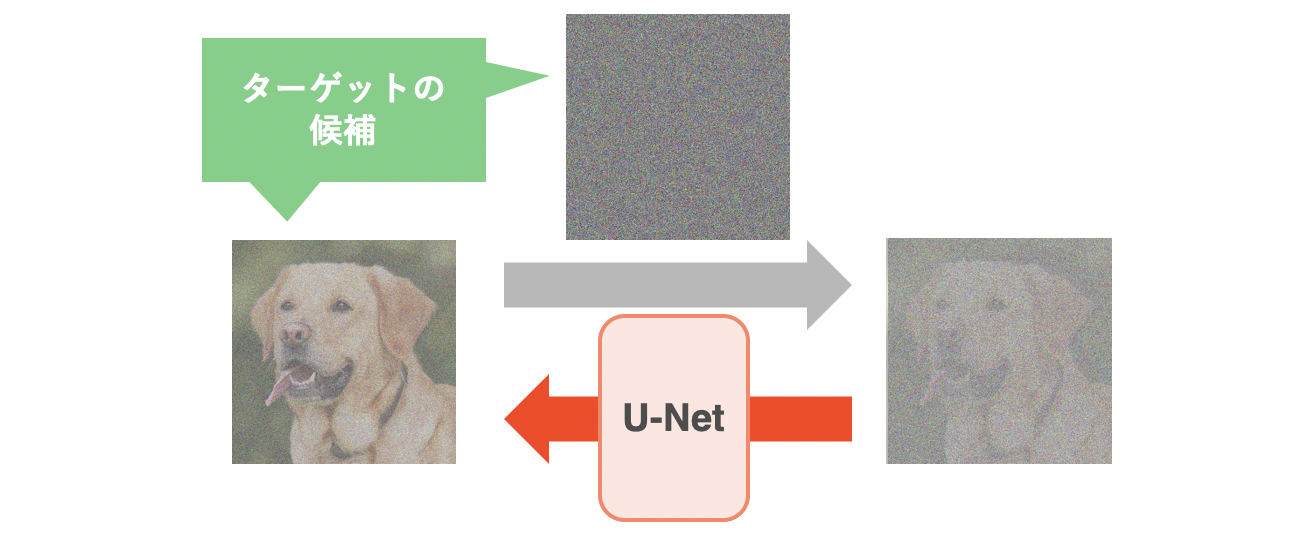
U-Netのターゲットの候補として画像とノイズがある。

まずは、U-Netのターゲット（＝U-Netに何を出力させるか）を決めなければいけません。ここまでの説明では、U-Netに画像を出力させていましたが、ターゲットの選択肢として考えられるものがもう1つあります。それは、拡散過程で加えたノイズです。先にネタバレしていたように、U-Netの学習では画像ではなく、拡散過程で加えたノイズをターゲットとします。これはDDPM[Ho, J. (NeurIPS'20)]の実験でノイズをターゲットとした方が生成画像のFIDスコアが良かったためです³。そのため、U-Netの入出力は以下のようになります。U-Netは入力ノイズから除去すべきノイズを出力します。出力されたノイズを入力ノイズから引き算することで、少しキレイな画像が手に入ります。

U-Netの予測対象は、「取り除くべきノイズ」

U-Netがノイズ$\mathbf{\epsilon}_t$を出力することはわかりました。あとは損失関数ですが、損失関数はシンプルに平均二乗誤差（MSE） です⁴。時刻$t$で加えたノイズを$\mathbf{\epsilon}$、U-Netを$\mathbf{\epsilon}_\theta$とすると、拡散モデルの損失関数$L_{\text{DM}}$は下式で与えられます。ここで$\theta$はU-Netの学習可能なパラメータです。

\begin{align}
L_{\text{DM}} := \mathbb{E}_{\mathbf{x}_0,\mathbf{\epsilon}, t}[\|\mathbf{\epsilon} - \mathbf{\epsilon}_\theta{\left( \mathbf{x}_t, t \right)} \|^2_2 ]
\end{align}

こちらの式を言葉で書き下しておきます。まず、キレイな画像$\mathbf{x}_0$、ノイズ$\mathbf{\epsilon}$、時刻$t$を選びます。$\mathbf{x}_0$はデータセットから、$\mathbf{\epsilon}$は標準正規分布$\mathcal{N}(0,1)$から、$t$は一様分布$\mathcal{U}(1, T)$からサンプリングします。その後、$\mathbf{x}_t$を用意します。詳細は割愛しますが、$\mathbf{x}_t$は$\mathbf{x}_0$に適量の$\mathbf{\epsilon}$を加えることで求められます。「適量」の値は、ノイズスケジューラを使えば簡単に求められます。こうして求めた$\mathbf{x}_t$と時刻$t$を$\epsilon_\theta$へ入力します。あとは、加えたノイズ$\mathbf{\epsilon}$とU-Netの出力$\mathbf{\epsilon}_\theta{\left( \mathbf{x}_t, t \right)}$の間で二乗誤差を計算します。この$L_{\text{DM}}$を最小化するようにU-Net $\mathbf{\epsilon}_\theta$を学習することで、最終的にノイズをうまく除去してくれるU-Netが手に入ります。

上図のような学習の流れをコードで見てみましょう⁵。$\mathbf{x}_t$はq_sampleという関数に用意させます。この関数の中では基本的に、キレイな画像とノイズを加重和し$\mathbf{x}_t$を獲得する、という処理をおこなっています。q_sampleの実装はこちら をご覧ください。コード中の変数名は基本的に上式と同じものを用いていますが、上式の$\mathbf{\epsilon}_\theta$はコード中ではわかりやすさのためunetとしています。また、コードの中では時刻$t$のサンプリングが$\mathcal{U}(0, T-1)$になっていることに注意してください。これは実装上の違いであり、中身は上式と同じです。

T = 1000
for x_0 in dataloader: # データをサンプリング
    # x_0: (B, C, H, W)=（バッチサイズ、チャネル数、高さ、幅）
    num_img = x_0.size(0) # 画像の数

    t = torch.randint(0, T, (num_img,)) # 時刻をランダムにサンプリング
    epsilon = torch.randn_like(x_0) # ガウシアンノイズ
 
    # x_0:キレイな画像、t:時刻、epsilon:ノイズ
    x_t = q_sample(x_0, t, epsilon) # x_tを用意 
    loss = F.mse_loss(epsilon, unet(x_t, t)) # 平均二乗誤差

2.4 U-Netによる生成

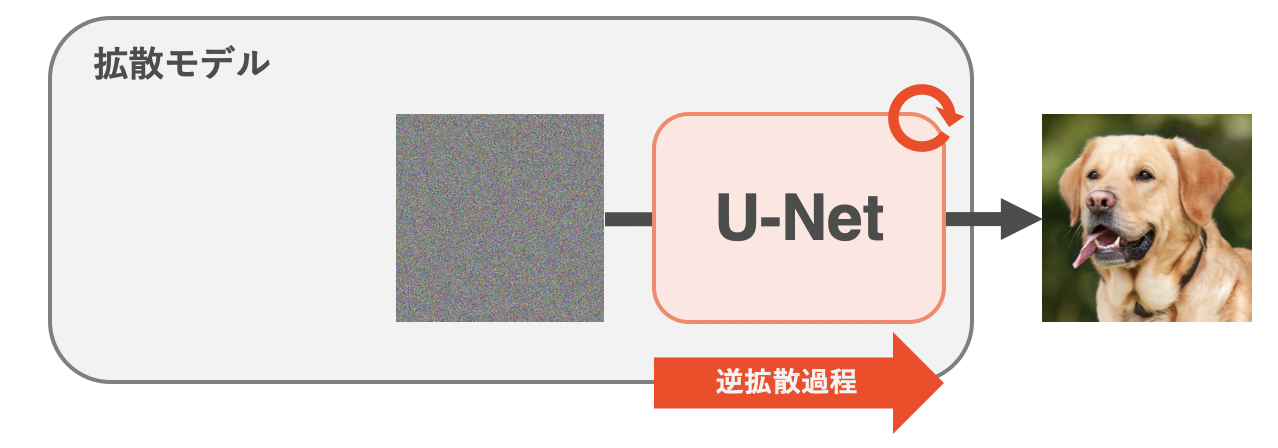
U-Netによる生成は、ガウシアンノイズからスタート

U-Netによる生成についてです。こちらは拡散過程は不要なので、上図のように拡散過程があった箇所がぽかんと抜けています。生成の際は、時刻$T$の完全なノイズ（＝ガウシアンノイズ）$\mathbf{x}_T$を始点としています。逆拡散過程によって少しずつノイズを除去していくだけです。具体的には、U-Netに時刻$t$におけるノイズ$\mathbf{\epsilon}_t$を推測させ、それをノイズ画像$\mathbf{x}_t$から引き算します。こうすることで、少しキレイな画像である$\mathbf{x}_{t-1}$が手に入り、最終的にキレイな画像$\mathbf{x}_0$を獲得できます。

ここでネックになってくるのが、生成時にはU-Netの順伝搬を$T$回繰り返すということです。Stable Diffusionの場合、$T=1000$などが用いられているため、このままだと1枚の画像を生成するためにU-Netを1,000回も通さないといけません。GANやVAEなどは生成時には1つのニューラルネットワーク（GANは生成器、VAEはデコーダ）を1発通すだけで画像を生成できることを考えると、拡散モデルが生成にいかに時間がかかるかが分かります。この「生成に時間がかかる」という問題に対しては、さまざまな対策が提案されています。例えば、単純に時刻を1個飛ばしや2個飛ばしすることで、サンプリングする時刻間引くRespacingや決定論的にノイズのサンプリングをおこなうDDIMなどがあります。こういった手法のおかげで、Stable Diffusionで1枚の画像を生成する際にはU-Netの順伝搬は50回程度で良いです（それでも多く感じるかもしれません）。拡散モデルによる生成の高速化手法などはソニーの方が解説しているこちらの動画で分かりやすくまとめられています。

それでは、生成の流れについてもコードで見ておきましょう。p_sample関数では、「U-Netによるノイズの推定」および「$\mathbf{x}_t$から推定したノイズを引き算」の2つを行なっています。これをforループで$T$回繰り返します。p_sampleの中の実装はこちらをご覧ください。

T = 1000
b, c, h, w = 1, 3, 768, 768

x = torch.randn(b, c, h, w)　# ガウシアンノイズ
for t in reversed(range(0, T)):
    x = p_sample(unet, x, torch.full((b,), t, dtype=torch.long), t) # 逆拡散過程の1ステップを進める（=時刻）
return x # 生成画像

2.5 小まとめ

拡散モデルの全体像

拡散モデルは拡散過程と逆拡散過程の2つの過程で成り立っていました。拡散過程では、画像に微小なガウシアンノイズを逐次的に加算します。一方、逆拡散過程では加算したノイズを逐次的に取り除いていきます。この「ノイズを取り除く」という処理をU-Netに任せてしまいます。U-Netの学習は、ノイズ画像を入力に受け取り、入力画像から取り除くべきノイズを出力するように学習されます。この時の損失関数は二乗誤差になります。U-Netによる生成時は、ガウシアンノイズからスタートし、そこから除去すべきノイズを学習済みのU-Netに出力させます。U-Netから出力されたノイズを、入力ノイズから引き算することで、ノイズを少し取り除きます。この操作を繰り返すことで最終的にキレイな画像を生成していきます。

3. VAE：潜在空間

ここまで拡散モデルを中心に話をしてきましたが、ここからはStable Diffusionの核心へと迫っていきます。拡散モデルによって画像を生成できることがわかりましたが、拡散モデルで高解像度の画像を生成しようとすると計算量の問題が避けて通れません。計算量が大きくなってしまうという問題を解決するためにStable DiffusionではVAEを用います。VAEの話に行く前に計算量問題へのもっと単純な解決方法について考えておきます。それは、そもそも生成する画像のサイズを小さくする、というものです。下の図のような感じです。

bilinearによる計算量削減

Bilinearなどで画像サイズを小さくして（パワポとかで画像サイズを小さくするイメージです。）、その画像に対して拡散モデルを学習させるということです。この拡散モデルの出力画像を再びBilinearなどで元のサイズに戻せば、計算量を増加させずに高解像度の画像を生成できます。しかし、もちろんこれでは「高解像度の画像生成」とは言えそうにないです。生成画像の解像度をBilinearで上げたところで、その画像のクオリティは全く高解像度のそれとは比べ物になりません。そこでBilinearの代わりにニューラルネットワークに画像のリサイズを任せることが考えられます。

VAEによる計算量削減

拡散モデルへの入力画像を小さくするニューラルネットをエンコーダ、拡散モデルの出力画像を大きくするニューラルネットをデコーダと捉えます。この「エンコーダー・デコーダ」構造として最適なニューラルネットワークこそが、Variational Autoencoder（VAE） です⁶。VAEは、Autoencoderの発展系のようなモデルです。一般的なAutoencoderは埋め込み空間に特別な制約はありませんでしたが、VAEでは埋め込み空間を正規分布に限定させています。VAEのエンコーダによって埋め込まれた潜在表現は、VAEのデコーダに通すことで元の画像（=ピクセル空間）に戻すことができます。VAEについてわかりやすく解説されている記事（Variational Autoencoder徹底解説など）がたくさんあるのでVAEの詳細はそちらを参照してください。ここでは、VAE（のエンコーダ）によって高次元の画像を低次元の潜在空間へと埋め込める、と理解しておいてください。Stable Diffusionで用いられているVAEの入力画像$\mathbf{x}_0$は$\mathbb{R}^{3\times H\times W}$、潜在表現$\mathbf{z}_0$は$\mathbb{R}^{4\times \frac{H}{8}\times \frac{W}{8}}$という次元になっています。VAEのおかげで元の画像を1/48倍のサイズにまで圧縮できています。また、U-Netの学習の際には、VAEはあらかじめ学習済みのものを使用します。

\begin{align}
L_{\text{LDM}} := \mathbb{E}_{\mathcal{E}(\mathbf{x}_0),\mathbf{\epsilon}, t}[\|\mathbf{\epsilon} - \mathbf{\epsilon}_\theta{\left( \mathbf{z}_t, t \right)} \|^2_2 ]
\end{align}

Stable Diffusionの損失関数も見ておきます。Stable Diffusionでは、この潜在表現に対してU-Netの学習を行います。このように潜在（Latent）空間で学習を行う拡散モデル(Diffusion Model)は、Latent Diffusion Model（LDM） と呼ばれます⁷。Stable Diffusion（というよりLDM）における損失関数$L_\text{LDM}$は上の式となります。$\mathcal{E}(\cdot)$はVAEのエンコーダのことで、$\mathbf{z}_0=\mathcal{E}(\mathbf{x}_0)$です。さきほどの拡散モデルにおける損失関数$L_\text{DM}$との違いは、拡散過程の対象が画像$\mathbf{x}$から潜在表現$\mathbf{z}$になっていることだけです。

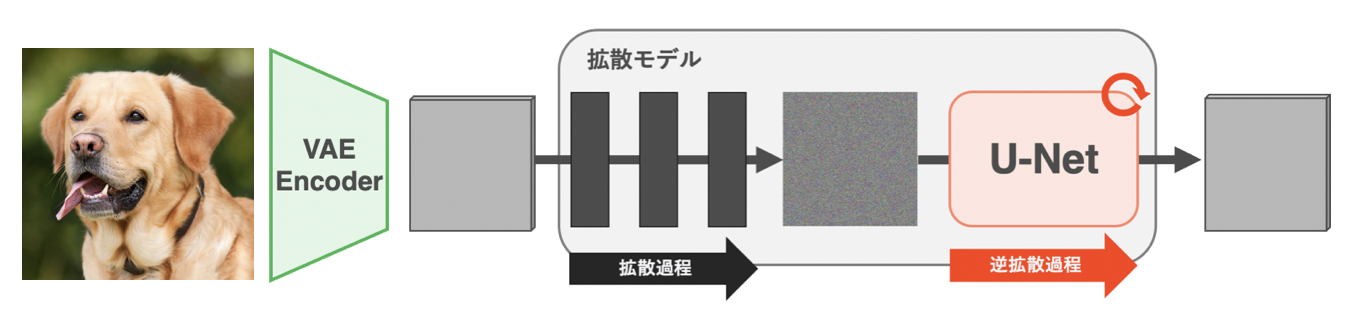
Stable Diffusionの学習時の挙動

学習時と生成時の挙動を図でまとめます。Stable Diffusionでは学習時は上図のようになります。画像はVAEのエンコーダで潜在空間に埋め込まれます。あとはその潜在表現を拡散過程に通し、その逆拡散過程をU-Netに学習させます。この学習の時に用いる損失関数がさきほどの式(2)です。

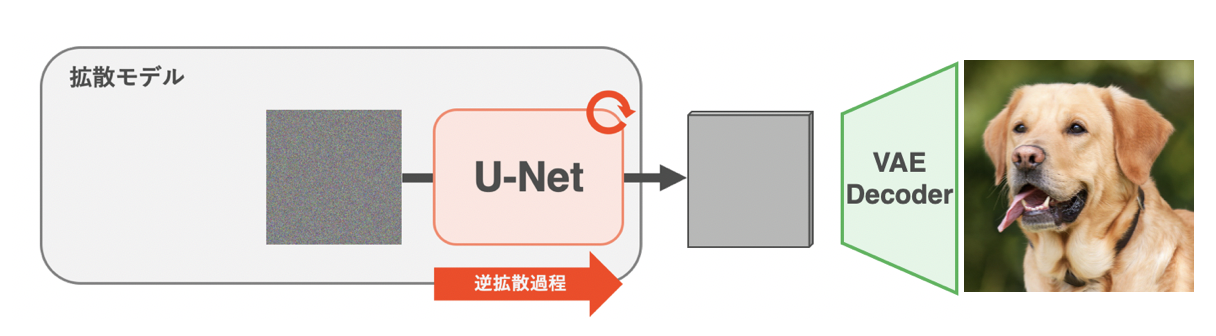
Stable Diffusionの生成時の挙動

一方、生成時はVAEのエンコーダや拡散過程などは不要になります。そのため、生成時の全体像は上の図のようになります。標準正規分布から時刻$T$のノイズをサンプリングし、学習済みのU-Netで少しずつノイズを除去します。そうして出来上がった（キレイな）潜在表現をVAEのデコーダに通すことで、最終的に画像を生成することが可能になります⁸。

ここまでで、U-NetとVAEを組み合わせることで、高解像度の画像を効率よく学習・生成できることがわかりました。あとは、Stable Diffusionの醍醐味である、テキストに沿った画像生成、についてです。この仕組みはU-Netのアーキテクチャを見ることでわかります。それでは、U-Netのアーキテクチャを見ていきましょう。

4. U-Netのアーキテクチャ

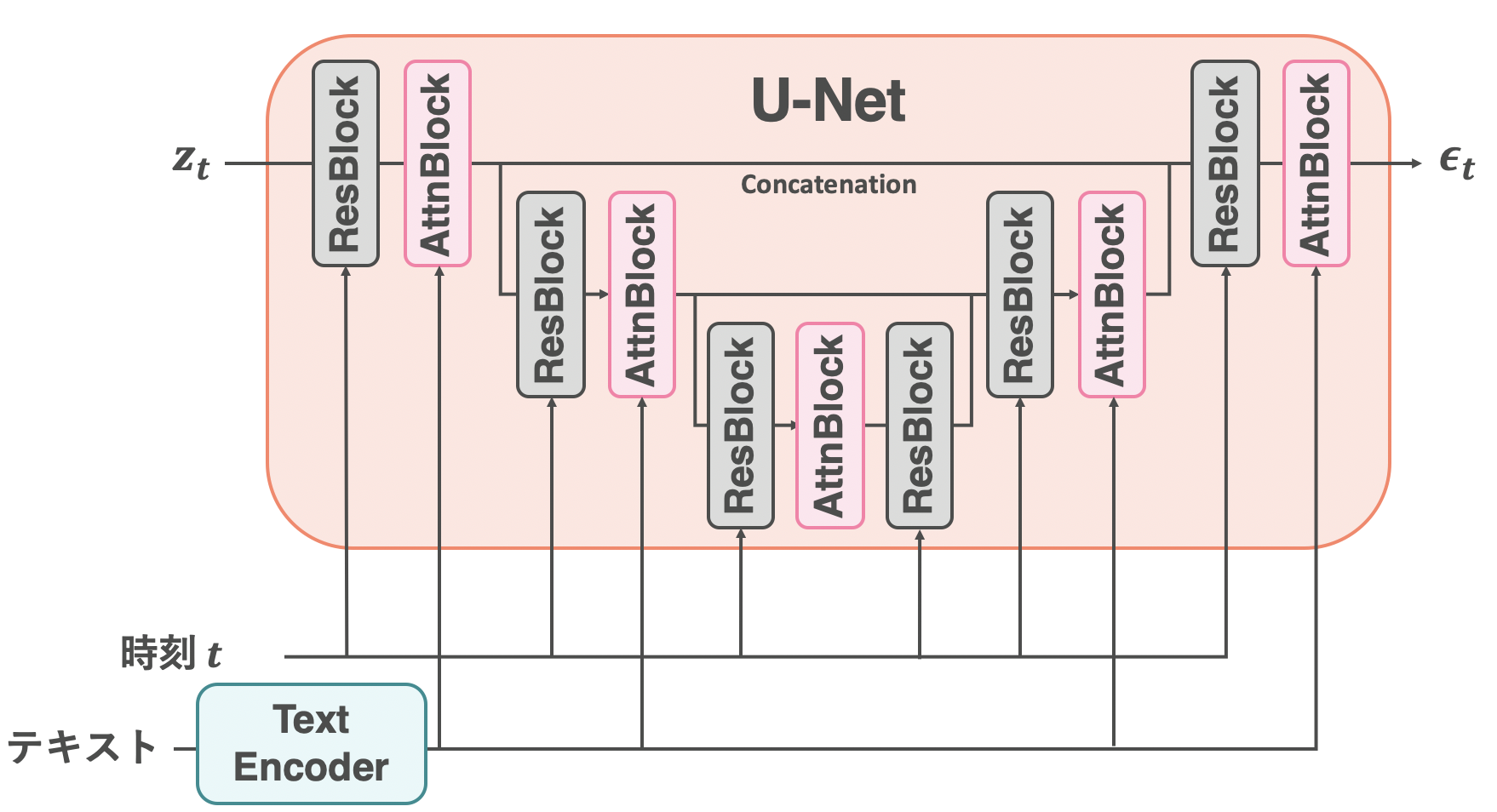
U-Netのアーキテクチャの全体像

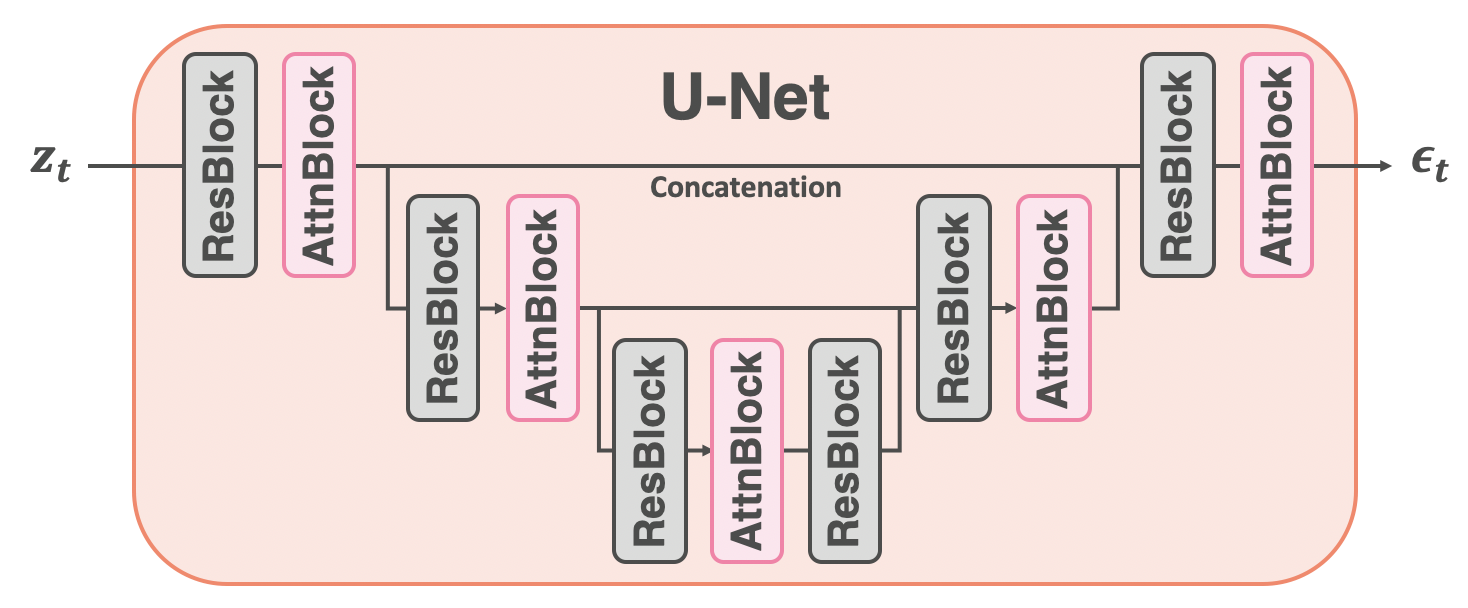
Stable Diffusionで使われているU-Netのアーキテクチャを見ていきます。上図はU-Netのアーキテクチャの概略図になります⁹。左から入力の潜在表現$\mathbf{z}_t$を受け取り、右から予測したノイズ$\mathbf{\epsilon}_t$を出力します。U-Netの中身は、「ResBlock」と「AttnBlock」を繰り返し用いる構造となっています。ResBlockやAttnBlockという名前は本記事でのみ便宜上用いるものです。ResはResidual、AttnはAttentionを指しています。それぞれの簡単な説明を以下に記します。

1. ResBlock: 畳み込み層を含んだモジュール。
2. AttnBlock: Attention層を含んだモジュール

時刻情報$t$はResBlockで、テキスト情報$y$はAttnBlockで組み込まれます。4.1節でResBlock（時刻による条件付け）について、4.2節でAttnBlock（テキストによる条件付け）について解説します。

4.1 ResBlock: 時刻による条件付け

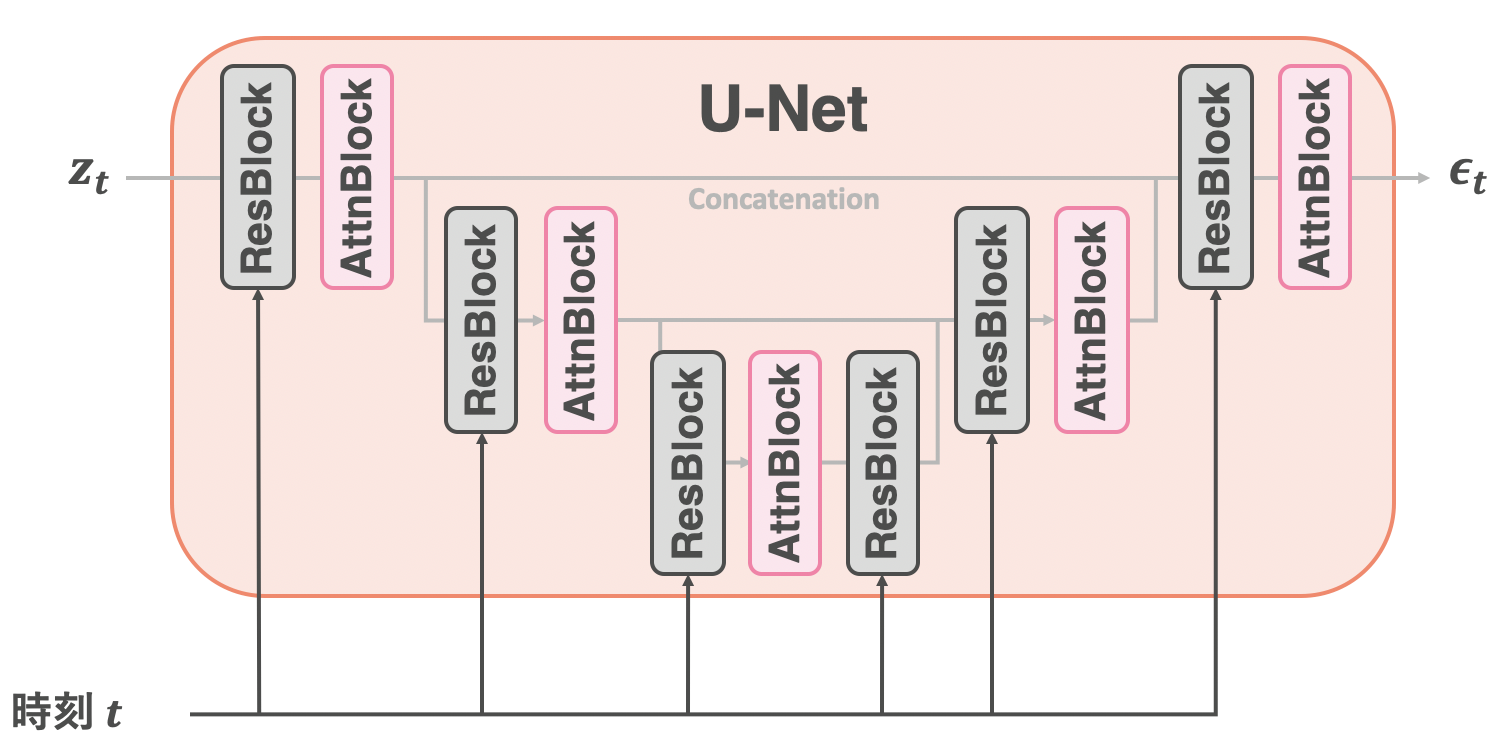
時刻はU-NetのResBlockで取り込まれる

ResBlockについてです。時刻$t$はこのResBlockで組み込まれます。まずはResBlockの中身を見ていきます。その後、ResBlockへの時刻$t$の組み込み方を2種類解説します。

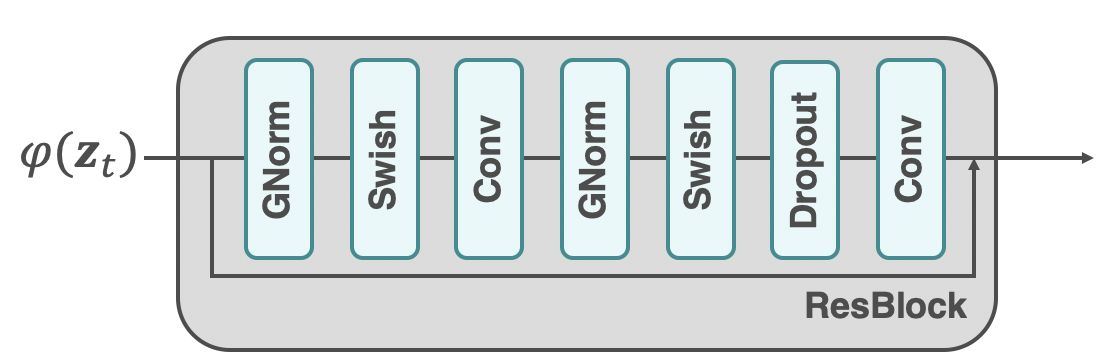
ResBlockの全体像

ResBlockの中身は上図のようになっています。GNormはGroup Normalizationを指しています。SwishやConv、Droupoutはその名の通り、活性化関数のSwish、畳み込み層、ドロップアウト層を指しています。そしてResBlockという名の通り、ResBlockへの入力が出力の直前で加算されています。

上図で「GNorm -> Swish -> Conv」を1つのかたまりとして見ると、ResBlockはこのかたまりが2つで構成されているものということが分かります（2つ目のかたまりにはDropoutが入っています。）。それでは、ResBlockへの時刻$t$の組み込み方法を見ていきます。

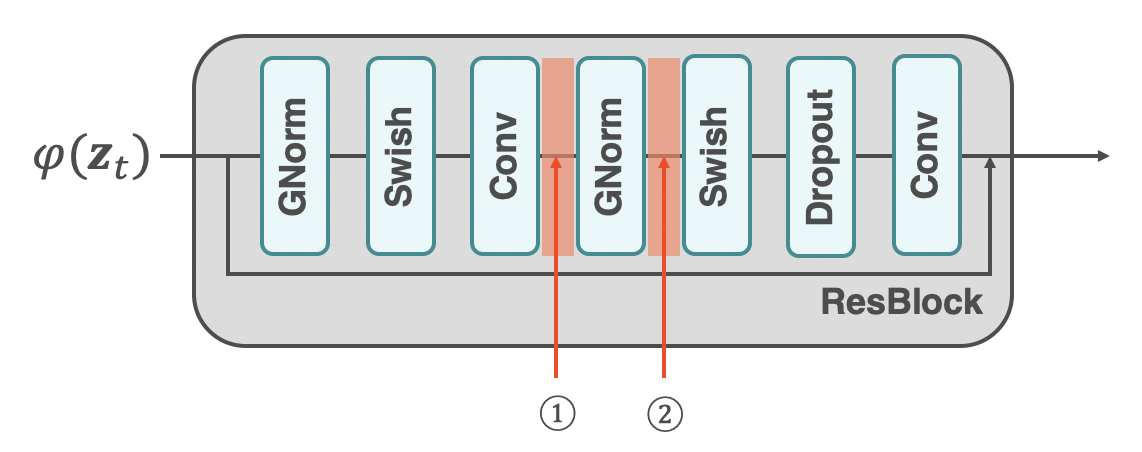
時刻の取り込み方法は2パターンある

Stable Diffusionでは時刻$t$の取り込ませ方として方法が2つあります。いずれも2個目のGNormの周辺で時刻$t$を取り込みますが、GNormの直前（上図①） で取り込むのかまたは直後（上図②) で取り込むのかという違いになります。DiffusersのStable Diffusionでは、①の方法で時刻が取り込まれています。それでは①から見ていきましょう。

時刻情報の取り込み方法①

まずは「①GNormの直前」についてです。上図のマス目はベクトルを表しています。こちらは非常にシンプルです。時刻$t$を線形層（Linear）に通した結果をGNormの直前に加算するだけです。

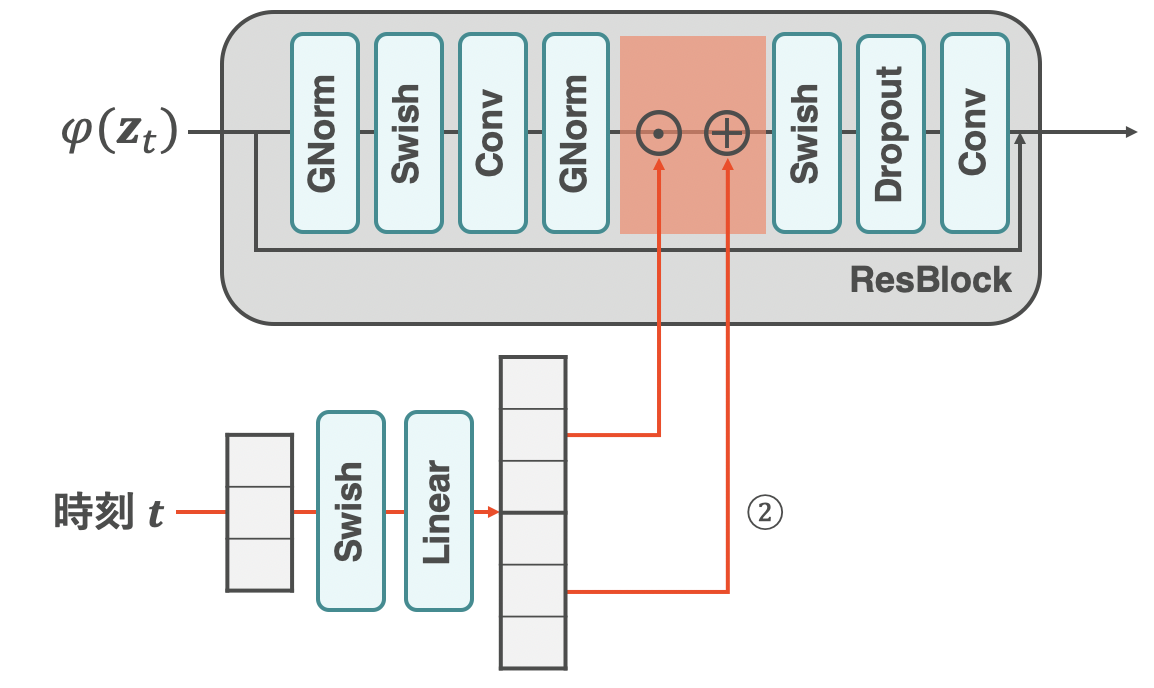
時刻情報の取り込み方法②

続いて「②GNormの直後」についてです。こちらもシンプルですが、取り込み方が先程とは少し異なります。時刻$t$を線形層に通すのは同じですが、この時の出力ベクトルは入力の2倍の長さになります。入力ベクトルの長さを$d$とすると出力ベクトルの長さは$2d$になる、ということです。上図では分かりやすさのため線形層の出力ベクトルの前半$d$と後半$d$をそれぞれ太枠で囲っています。長さ$2d$のこの出力ベクトルの前半$d$のベクトルをResBlockの方に掛け算します。このとき掛け算は要素積です。続けて後半$d$のベクトルを加算させます。これはAdaptive GroupNorm（AdaGN） と呼ばれ、下式のように式で表すとより分かりやすいです。$\mathbf{\gamma}$が前半$d$のベクトル、$\mathbf{\eta}$が後半$d$のベクトルを指しています。$\text{GN}(\cdot)$はGroup Normalization、$h$はU-Netを流れる潜在ベクトルです。

\begin{align}
\text{AdaGN}(\mathbf{h}) = \mathbf{\gamma} \odot \text{GN}(h) + \mathbf{\eta} 
\end{align}

4.2 AttnBlock: テキストによる条件付け

テキストはU-NetのAttnBlockで取り込まれる。(中間層は常にSelf-Attention（コード）)

追記: 中間層においては、常にSelf-Attention（あるふさんに教えていただきました。）

つづいてAttnBlockついて見ていきましょう。入力テキストはAttnBlockによって組み込まれる前にText Encoderを通ります。これによってテキストがベクトルに変換されます。こうしてベクトルに変換されたテキストがAttnBlockによってU-Netへと組み込まれます。まずText Encoderについて説明をします。その後、AttnBlockの中身を見ていきます。

4.2.1 Text Encoder：CLIPについて

Text Encoderの役割は、テキストをベクトルに変換することです。Text Encoderとして、学習済みのTransformerを使います。Transformerはデコーダのみのアーキテクチャ（＝GPT系）で、Transformerの最終層の出力をAttnBlockに取り込ませます。Text Encoder自体には特別なことはないのですが、最大の特徴は、その学習方法です。Text EncoderであるTransformerの学習にはCLIP[Radford, A.(ICML'21)]と呼ばれる手法が用いられています。ここでは、CLIPについて簡単に説明をします。

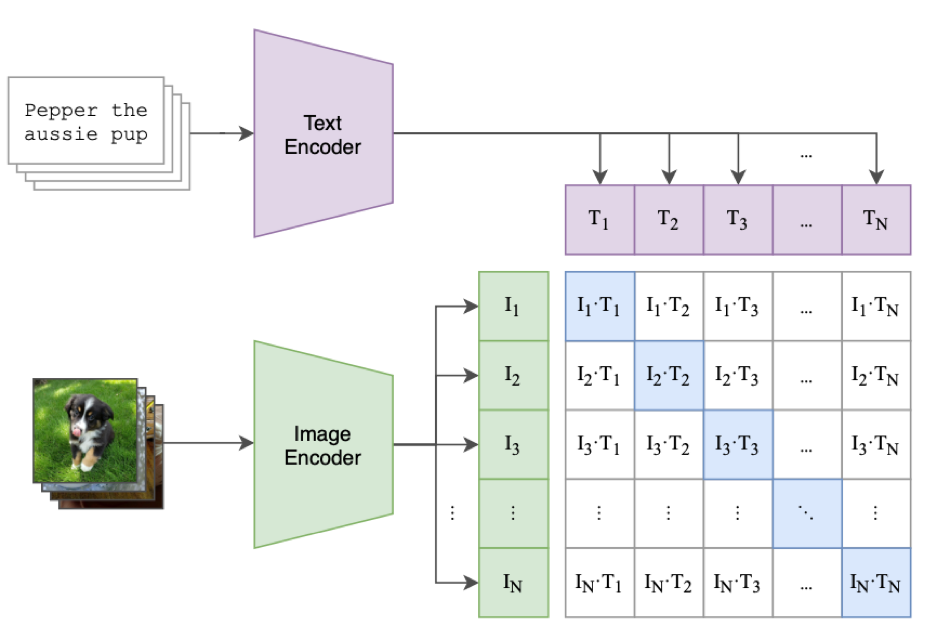
[Radford, A.(ICML'21)] 図1より引用

CLIPの仕組みは非常に単純です。CLIPとは、画像とテキストを同じ空間に埋め込む学習方法になります。上図はCLIPの学習方法を示した図になります。学習には、テキストと画像のペアを用います。上図の例では、$N$個のペアを用いたミニバッチ学習になっています。テキストのうち一番手前にある「Pepper the aussie pup」という文と子犬の画像がペアになっています¹⁰。テキストはText Encoder（Transformer）によってベクトル$T_i$に、画像はImage Encoder（ResNet）によってベクトル$I_i$に埋め込まれます¹¹。$T_i$としてTransformerの最終層の[EOS]トークンなどが用いられます。$I_i$の候補としてResNetの最終層の出力をGlobal Average Poolingに通してできたベクトルなどが考えられます。¹²。上の図では、$T_1$と$I_1$はそれぞれ「Pepper the aussie pup」と子犬の画像に対応しています。それ以外はミニバッチ内の別のテキストおよび画像たちの埋め込みベクトルです。あとは、$T_i$と$I_i$の全ての組み合わせで内積をとると、図中の行列が出来上がります。本来のペア同士（子犬の例なら、$T_1$と$I_1$）である対角成分の値が大きく、それ以外の内積（子犬の例なら例なら、$T_1$と任意の$I_k (k\neq 1)$の内積）は小さくなるように、損失をとります。これは、各行および各列で、対角成分の要素を1としたラベルに対してクロスエントロピー損失をとることで実現できます。

ちなみにCLIPで学習したImage Encoderは、従来のモデルよりも非常にロバストであること（例えば、「バナナの写真」と「バナナのスケッチ」のようなドメインシフトが起こっていても、両方ともしっかり「バナナ」として認識してくれる。）がCLIPの論文で示されています。StableDiffusionでは、CLIPによって学習したText Encoder（Transformer）を用いてテキストをベクトルに埋め込みます。それでは、このベクトルをU-Netの中にどう取り込んでいくかを見ていきましょう。

4.2.2 AttnBlock

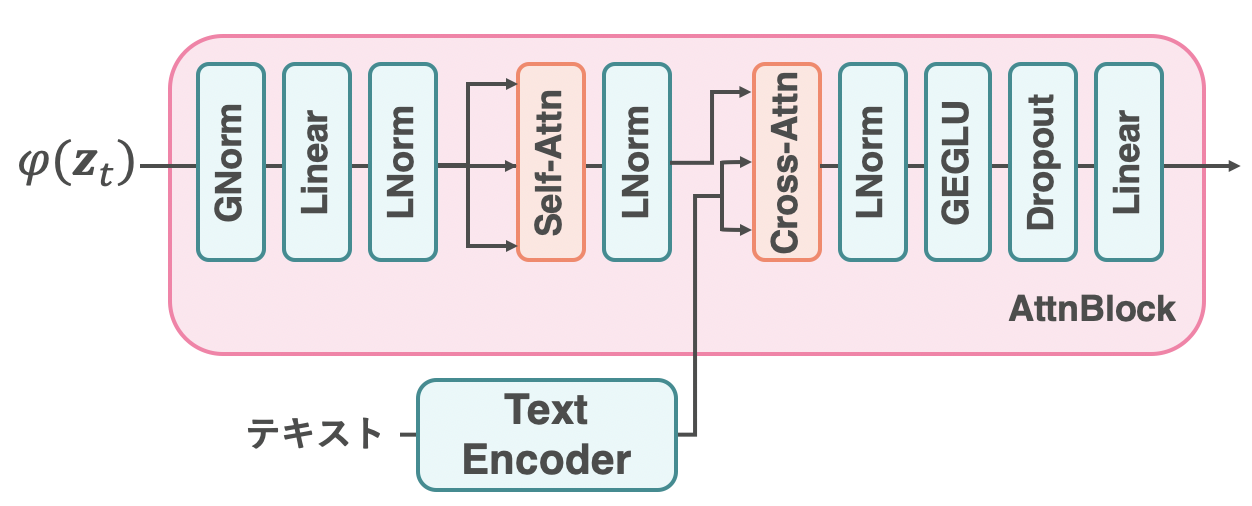
AttnBlockの全体像

AttnBlockの中身は上図のようになっています。ごちゃごちゃと書いてありますが、AttnBlockは、「Self-Attention」と「Cross-Attention」の2つが重要です（図中、橙色）¹³。それ以外はただの線形層やノーマライゼーション層です。CLIPによって学習されたText Encoderの出力は、Cross-Attentionで取り込まれています。テキストによる条件付けは、Cross-Attentionで行われています。それでは、Self-AttentionとCross-Attentionについて簡単に説明します。

追記: 中間層においては、常にSelf-Attention（あるふさんに教えていただきました。）

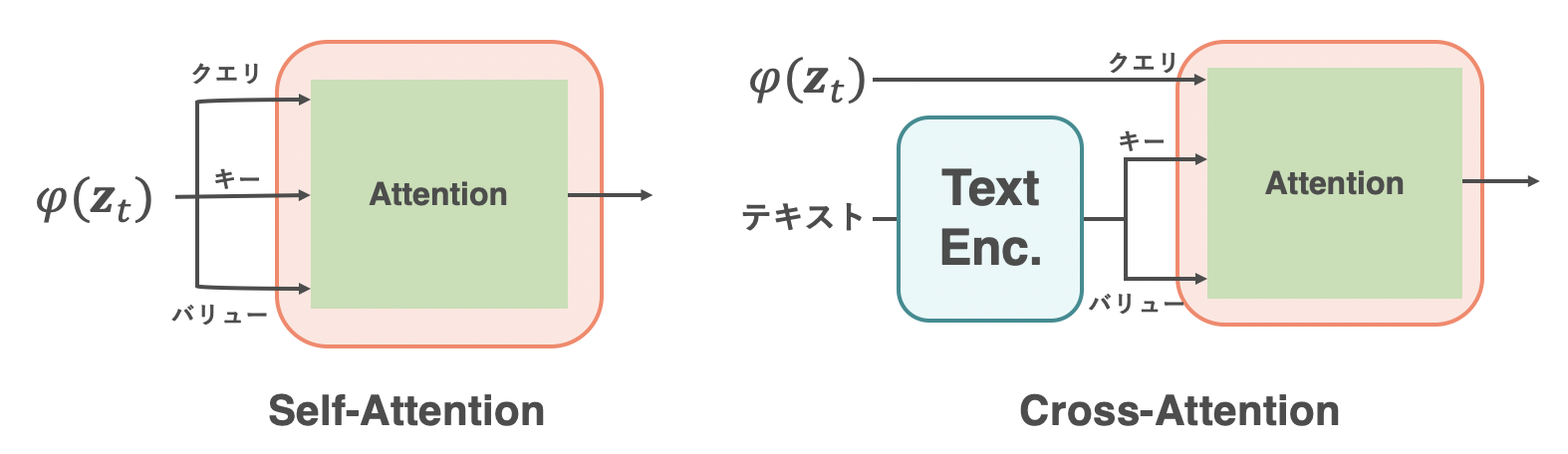
Self-AttentionとCross-Attention

左図はSelf-Attention、右図はCross-Attentionを表しています。$\varphi\left(\mathbf{z}_t\right) \in \mathbb{R}^{N\times d_{\epsilon}}$は、$\mathbf{z}_t$のU-Netにおける中間表現（を1次元ベクトルにflattenしたもの）を指しています。Attentionは、Dot-product Attention（＝QKVのAttention）を指しています。Self-AttentionとCross-Attentionで異なる点は、Attentionへの入力（＝クエリ、キー、バリュー）をどこから持ってくるかという点のみです。Self-Attentionのクエリ、キー、バリューは、いずれも同じ$\varphi\left(\mathbf{z}_t\right)$です。その一方でCross-Attentionは、クエリのみが$\varphi\left(\mathbf{z}_t\right)$で、キーおよびバリューはテキストの埋め込みになっています。このテキストの埋め込みは、Text Encoder（Transformer）の最終層の出力が使われています。Attentionはバリュー（＝テキストの埋め込み）の加重和が出力となるので、テキスト情報が組み込まれていることがわかります。

Self-AttentionおよびCross-Attentionを定式化しておきます。まずAttentionですが、クエリ、キー、バリューをそれぞれ$Q \in \mathbb{R}^{N\times d}$、$K\in\mathbb{R}^{N\times d}$、$V\in\mathbb{R}^{N\times d}$とすると、Attentionは下式で定義されます。$\text{softmax}$はソフトマックス関数、$N$はトークン数、$d$は埋め込みベクトルの長さです。

\begin{align}
\text{Attention}(Q, K, V)=\text{softmax}\left( \frac{QK^T}{\sqrt{d}}\right)V
\end{align}

Self-AttentionとCross-Attentionは、キーとバリューの作り方に違いがありました。Self-Attentionではクエリ、キー、バリューがすべてU-Netの中を通る$\varphi\left(\mathbf{z}_t\right) \in \mathbb{R}^{N\times d_{\epsilon}}$から作られます。これは式で表すと下のようになります。ここで$W_Q \in \mathbb{R}^{d_\epsilon \times d}$、$W_K \in \mathbb{R}^{d_\epsilon \times d}$、$W_V \in \mathbb{R}^{d_\epsilon \times d}$はそれぞれクエリ、キー、バリューを作るための線形層の重みです。

\begin{align}
Q &= \varphi\left(\mathbf{z}_t\right) W_Q\nonumber \\
K &= \varphi\left(\mathbf{z}_t\right) W_K\\
V &= \varphi\left(\mathbf{z}_t\right)W_V \nonumber \\
\end{align}

一方で、　Cross-Attentionではクエリが$\varphi\left(\mathbf{z}_t\right)$、キーとバリューがテキストの埋め込みから作られていました。$M$個のトークンを持つテキスト（$\approx$ $M$個の"単語"で構成された文）を$y$、Text Encoder（＝Transformer）を$\tau_\theta\left(\cdot\right)$とし、テキストの埋め込みベクトルを$\tau_\theta\left(y\right)\in\mathbb{R}^{M\times d_\tau}$とします（Stable Diffusionでは、$M=77, d_\tau=768$が用いられています）。Cross-Attentionにおけるクエリ、キー、バリューは下のようになります。当然ですが、$W_K \in \mathbb{R}^{d_\tau \times d}$および$W_V \in \mathbb{R}^{d_\tau \times d}$の次元は、テキストの埋め込みベクトルに合わせた形（つまり、$d_\tau \times d$）になります。

\begin{align}
Q &= \varphi\left(\mathbf{z}_t \right) W_Q\nonumber \\
K &= \tau_\theta\left(y \right) W_K \\
V &=  \tau_\theta\left(y \right)W_V  \nonumber \\
\end{align}

Self-AttentionとCross-Attentionを用いることで、AttnBlockの完成となります。繰り返しになりますが、Self-AttentionとCross-Attentionの違いは、キーおよびバリューの作り方だけです。今回は、キーおよびバリューをテキストの埋め込みベクトルとしましたが、たとえばセグメンテーションマップの埋め込みベクトルをキーおよびバリューとすれば、そのセグメンテーションマップを条件とした画像生成ができます。これによって画像-画像変換（Image-to-Image Translation）なども可能になると言うことです。

4.3 小まとめ

U-Netのアーキテクチャ

本章では、U-Netのアーキテクチャを見てきました。U-Netは、画像の潜在表現$\mathbf{z}_t$を入力として受け取り、それをキレイにするためのノイズ$\mathbf{\epsilon}_t$を出力してくれます。U-Netは、大きく「ResBlock」と「AttnBlock」で構成されています。「ResBlock」は主に畳み込み層で構成され、時刻情報はここで取り込まれます。一方、「AttnBlock」は主にSelf-AttentionとCross-Attentionで構成され、テキスト情報はCross-Attentionで取り込まれます。

5. Stable Diffusion

ここまでStable Diffusionの仕組みについて解説してきました。この章では、Stable Diffusionの全体像を簡単におさらいし、実際にStable Diffusionを動かしてみます。Stable Diffusionを動かすのは、Diffusersというライブラリが用意されているため非常に簡単です。

5.1 Stable Diffusionの全体像

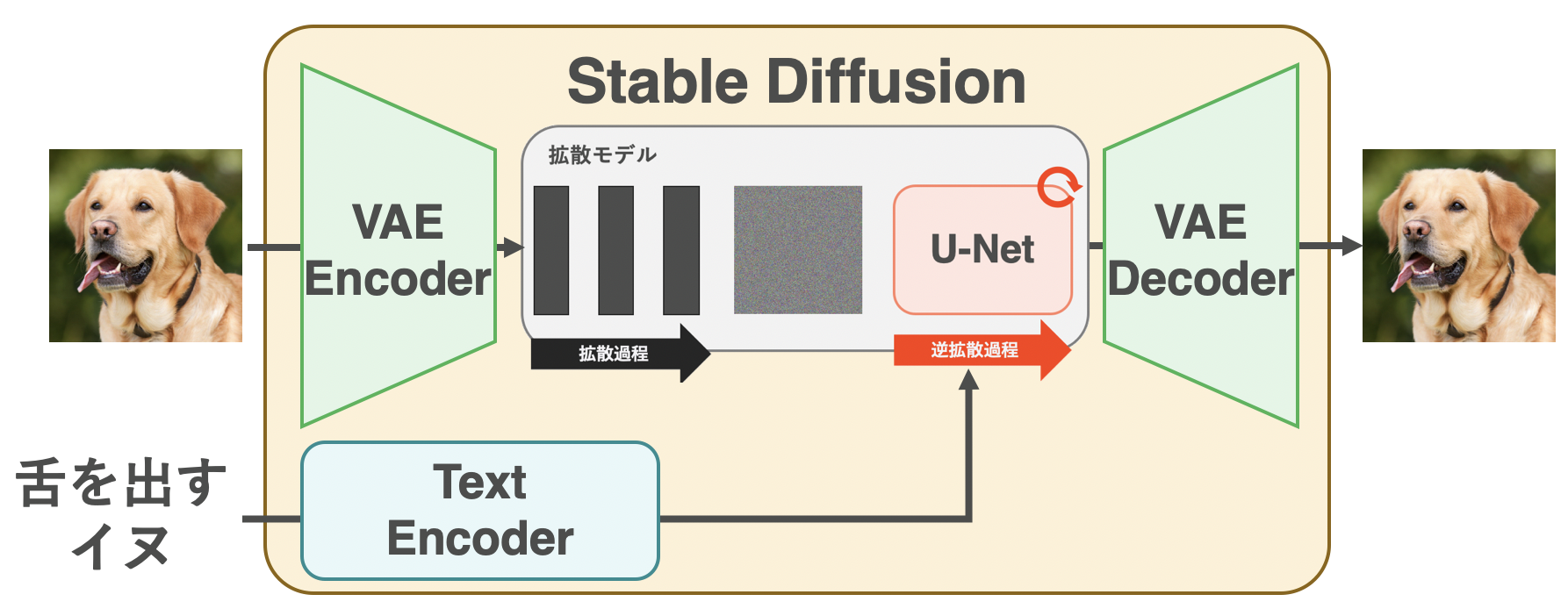
Stable Diffusionの学習時の挙動

まずはStable Diffusionの学習時の挙動です。上の図に示した通り、入力として画像とテキストのペアを受け取ります。画像はVAE Encoder、テキストはText Encoderによって埋め込まれます。潜在空間へと埋め込まれた画像は、拡散モデルの拡散過程および逆拡散過程を通っていきます。拡散過程では、画像の潜在表現がノイズになるまで微小のガウシアンノイズを繰り返し加算します。逆拡散過程はその逆で、ノイズから少しずつガウシアンノイズを除去します。この除去は、U-Netに学習させます。U-Netの最終的な出力はVAE Decoderに通ることで元の画像を復元できるようになります。

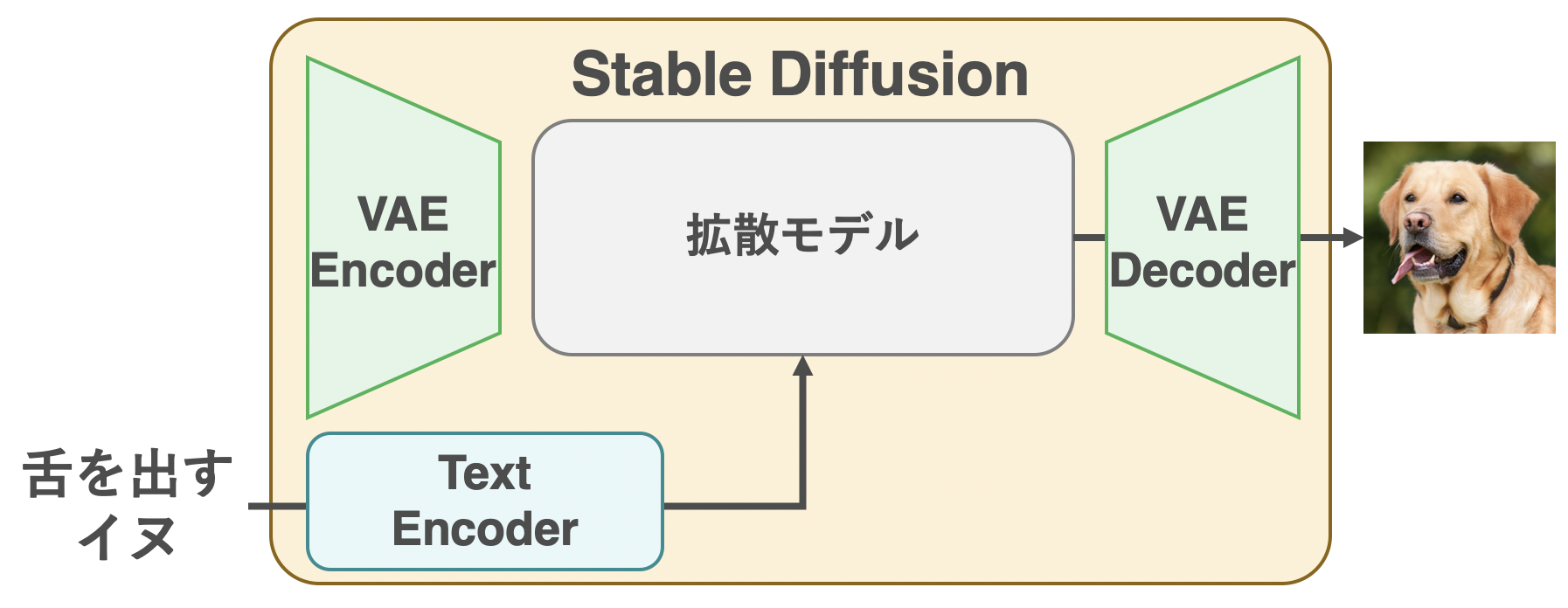
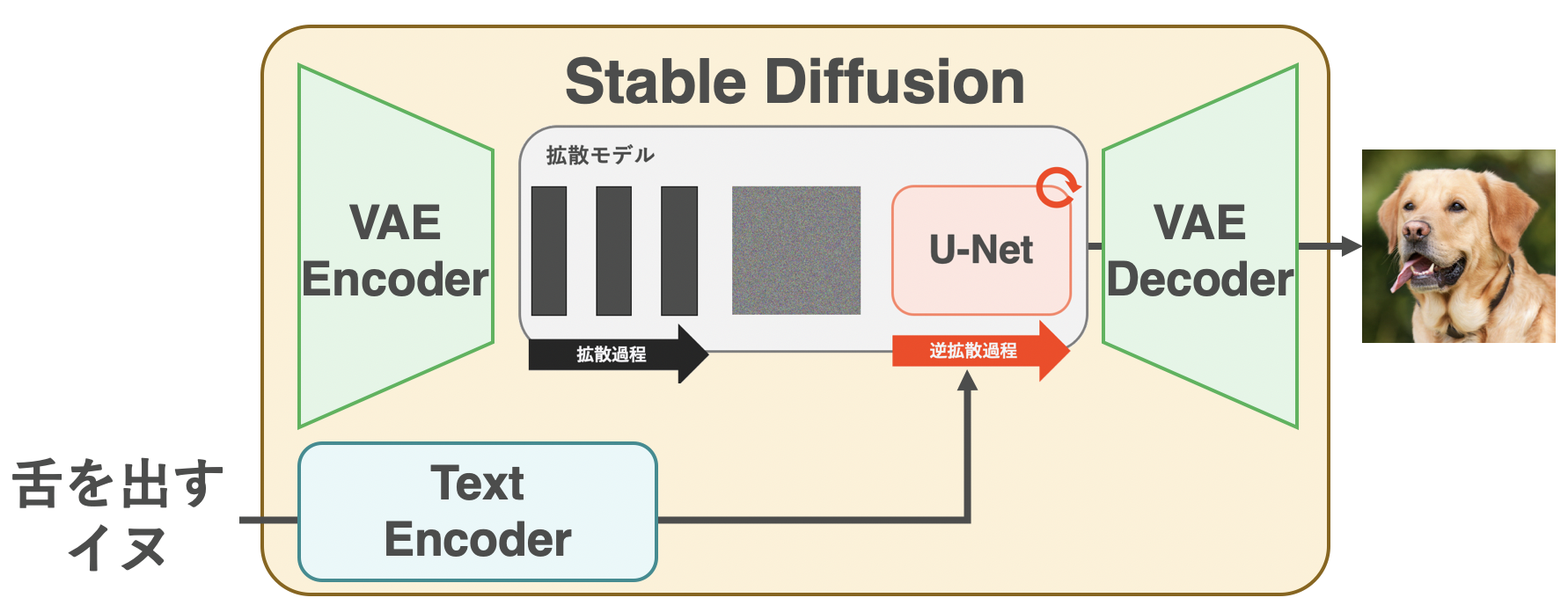
Stable Diffusionの生成時の挙動

一方、生成時はテキストだけが入力となります。このテキストを逆拡散過程のU-Netへと入力することで、U-Netが任意のガウシアンノイズから少しずつノイズを除去してくれます。このとき、U-Netは入力テキストによって条件付けがされているため、出力される画像の潜在表現は、テキストに沿ったものになります。最後にU-Netの最終的な出力をVAE Decoderに通すことで、テキストに沿った画像を生成できるようになります。学習済みのStable DiffusionはHugging Faceに用意されており、Diffusersで簡単に使うことができます。それでは、実際にStable Diffusionを動かしてみましょう。

5.2 Stable Diffusionを動かす

Stable Diffusionを動かすのは非常に簡単です。GPUの環境は、Google Colaboratoryなどで十分です（Colab上で動かせるのも、Stable DiffusionがVAEの力を使って計算量を抑えてくれているからですね）。あとは、Hugging Faceに書いてあるコード例を動かすだけです。

まずは必要なライブラリをpipで入れます。

pip install --upgrade git+https://github.com/huggingface/diffusers.git transformers accelerate scipy torch

インストールしたら、下のコードを動かします。

from diffusers import StableDiffusionPipeline, EulerDiscreteScheduler
import torch

# Stable Diffusion v2のモデル名
model_id = "stabilityai/stable-diffusion-2"

# ノイズスケジューラ
scheduler = EulerDiscreteScheduler.from_pretrained(model_id, subfolder="scheduler")
# 重みのダウンロード & モデルのロード
pipe = StableDiffusionPipeline.from_pretrained(model_id, scheduler=scheduler, revision="fp16", torch_dtype=torch.float16)
# GPU使用。（CPUだと生成にかなり時間かかります。というかいつ終わるのか不明。）
pipe = pipe.to("cuda")

# 入力テキスト
# 訳：スタバで四苦八苦しながら論文を読んでいるロボット
prompt = "a robot struggling with reading through a scientific paper at Starbucks"
image = pipe(prompt).images[0]  

生成した画像はimage変数の中に入っています。実際に生成された画像は下のようになりました。しっかりと腕を組んでいて、ロボットの困っている感がでています！皆さんもいろいろなテキストを試してみてください！

四苦八苦しながら論文を読んでいるロボット（Stable Diffusionで生成）

ちなみに、pipeの中身を見てみると、本記事で解説したU-Net、VAE、Text Encoderたちが入っていることが分かります。

print(pipe)

StableDiffusionPipeline {
  
  ...
  
  "text_encoder": [
    "transformers",
    "CLIPTextModel"
  ],
  
  ...

  "unet": [
    "diffusers",
    "UNet2DConditionModel"
  ],
  "vae": [
    "diffusers",
    "AutoencoderKL"
  ]
}

6. まとめと所感

本記事では、Stable Diffusionの仕組みとその動かし方を見てきました。Stable Diffusionは、拡散モデル（U-Net）とVAEを組み合わせたようなモデルで、計算量を抑えたまま高解像度の画像生成を達成していることがわかりました。Stable Diffusionの可能性は止まるところを知らず、画像拡張や動画変換などにも応用されています。Stable Diffusionは、Google Colaboratoryなどで手軽に試せるので、ぜひ使ってみてください！

Twitterで人工知能のことや他媒体の記事などを紹介していますので@omiita_atiimoもご覧ください。

7. 参考

• "High-Resolution Image Synthesis with Latent Diffusion Models", Rombach, R., Blattmann, A., Lorenz, D., Esser, P., Ommer, B., (CVPR'22)
  • Latent Diffusion Modelの論文。Stable Diffusionの元となっている論文。
• "Denoising Diffusion Probabilistic Models", Ho, J., Jain, A., Abbeel, P., (NeurIPS'20)
  • DDPMの論文
• "Improved Denoising Diffusion Probabilistic Models", Nichol, A., Dhariwal, P., (ICML'21)
  • Improved DDPMの論文
• Diffusion Models | Paper Explanation | Math Explained
  • 拡散モデル全体の流れおよび数式の解説。数式の導出は一見の価値あり。
• What are Diffusion Models?
  • 安定の解説
• The Annotated Diffusion Model
  • Hugging Faceによる、DDPMの物凄くわかりやすいコード付き解説
• 【Deep Learning研修（発展）】データ生成・変換のための機械学習　第７回前編「Diffusion models」
  • ソニーによる、拡散モデルの全体の流れ
• Stable Diffusion: High-Resolution Image Synthesis with Latent Diffusion Models | ML Coding Series
  • Stable Diffusionのコードをかなり詳細に解説。
• CompVisによるStable Diffusionの公式実装
• DiffusersにおけるStable Diffusionの実装

1. Stable Diffusionは、テキスト以外に画像なども入力として受け取ります。本記事ではStable Diffusionの一番スタンダードな使い方であろう「テキストから画像への変換」を例にStable Diffusionの中身を解説します。他の入力であっても中身はほとんど変わりません。 ↩

2. この図の矢印は生成時の挙動を示しています。学習および生成時のそれぞれの挙動についてはこの先で詳しく解説します。 ↩

3. 拡散過程の各時刻の平均$\mathbf{\mu}_t$で損失を取ることは、ノイズ$\mathbf{\epsilon}_t$で損失を取ることと等価です。そのため、実験的に良かった、「ノイズをターゲットにする」というのを採用しています。詳しくは[Ho, J. (NeurIPS'20)]の式(11)を参照してください。 ↩

4. ノイズとの二乗誤差、というのは「データに対する尤度を最大化したい」という目的から数学的に導かれたものです。詳しくはこちらの動画が非常にわかりやすく解説してくれています。一応、私の理解をここに書いておきます（間違っていたら教えていただけると大変助かります。。）。まず、データ$\mathbf{x}_0$に対する対数尤度$\log(p_\theta(\mathbf{x}_0))$を最大化する際に、潜在変数やらマルコフ連鎖やらを仮定します（この仮定が拡散モデルたらしめている？）。そこから対数尤度のELBOを式変形していくと、「ELBOの最大化＝各時刻のKLダイバージェンスの最小化」であることが導けます。ここで、KLダイバージェンスはサンプリングされたノイズの分布と生成モデルによって推測された分布の間でとります。これは正規分布同士のKLダイバージェンスであり、拡散過程の時に分散は既知としているため、平均の二乗誤差ということになります。あとは、平均を展開すると、加えたノイズとの二乗誤差を最小化しても同じであることが分かります。あとは実験的に「ノイズとの二乗誤差」が「平均との二乗誤差」よりも良かったので、ノイズとの二乗誤差を最終的な損失関数としています。 ↩

5. Hugging Faceの非常に分かりやすい記事の学習コードを編集したものを載せています。 ↩

6. Stable Diffusionの元となっている論文[Rombach, R.(NeurIPS'22)]では、VAEの他にVQ-VAEでも実験を行なっている。 ↩

7. Stable Diffusionの元となっている論文[Rombach, R.(NeurIPS'22)]のタイトルは「High-Resolution Image Synthesis with Latent Diffusion Models」であり、LDMによる高解像度の画像生成を行なっていることが分かります。 ↩

8. ちなみに、ほかの拡散モデルであるDALL-E 2やImagenでは、Bilinearなどで小さくした画像に対して拡散モデルを学習させています。そして、出力された低解像度の生成画像を超解像モデルを用いることで高解像度にします。超解像モデルにも拡散モデルが用いられています。 ↩

9. 本記事では、Stable DiffusionのアーキテクチャとしてdiffusersのStableDiffusionPipelineを参考にしています。各モジュールの正確な数など、細かい実装はコードを参照してください。 ↩

10. pupとはpuppy（子犬）のことですね。 ↩

11. CLIPはあくまで学習方法の名前なので、Text EncoderやImage Encoderとして、Word2VecやVision Transformerなど任意のアーキテクチャを使えます。 ↩

12. 実際のCLIPの論文では、GAPではなくAttention Poolingと呼ばれるプーリング手法が使われています。これは、QKVのSelf-Attentionで、クエリはGAPによる埋め込みベクトルになっています。キーとバリューはResNetの出力をそのまま使います。ResNetの出力を、チャネル方向のベクトルたちの集まりとして見れば、QKVを使って1つのベクトルに集約できることがわかります。 ↩

13. 図では省略しましたが、実装ではSelf-AttentionおよびCross-Attentionなどの前後にスキップ結合があります。 ↩