東京での感染爆発をざっくり予測する

更新履歴

　2020/4/7 新記事へのリンクを追加しました。

はじめに

　老技術者は新型コロナに感染したらひとたまりもない満身創痍の古老であります。妻は私に感染させようと日々東京に出向いてウィルスをかき集めては埼玉の我が家に運搬しております。というのは悪い冗談であってほしい今日この頃。
　高校数学を使って、妻が毎日東京へ行くことがどれほど危険なことか示したいと思います。

環境: Windows10 Pro 64bit + anaconda + Python 3.7.3

(1) 基本式

　感染症というのはウィルスを持っている「感染源候補者」からある割合で感染して自分も「感染源候補者」となるわけです。ということは「感染源候補者」が多ければ多いほど「感染源候補者」の増え方も激しくなるのは明らかですよね。そこでここでは単純化して、「1日当たりの感染源候補者の増分は、その前日～n日前に存在した感染源候補者の人数に比例する」という仮定を置くことにします。

「感染源候補者数」$N$は潜伏期間（14日間と仮定します）の2倍すなわち直前28日間に陽性と報告された人数とします。
$\frac{dN}{dt}$は1日当たりの「感染源候補者数」の増分となります。
これが「感染源候補者数」に比例すると仮定した微分方程式は、

\frac{dN}{dt}=\kappa N

となります。ここで、$\kappa$は１日当たり「感染源候補者数」を何人増やすかを表します。
この一般解は、

N=A e^{\kappa t}\;\; (Aは積分定数)

となります。$k>0$ならば、$t$が増えるにつれ恐ろしい勢いで増えていくのがこの関数の特徴です。後ほどその恐ろしさを実感する数値実験をします。

(2) データの読み込み

東京都の感染症データはここにあります。
https://stopcovid19.metro.tokyo.lg.jp/

若いころからけっしてまっすぐな道を歩んで来なかった老技術者はこのサイトで「梅毒」なる文字に一瞬怯むわけですが、そこはぐっと体勢を立て直して新型コロナのデータを探します。あった。
https://stopcovid19.metro.tokyo.lg.jp/data/130001_tokyo_covid19_patients.csv

日次で更新してくれている。まずはこれをpandasに食わせます。
その前にimportしときましょ。

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from datetime import timedelta
import datetime
import matplotlib.dates as mdates
from matplotlib.font_manager import FontProperties
import math

日本語を使うおまじないして、定数も見やすいところに置いておきます。フォントのttcファイルの場所は各自の環境に合わせてくださいね。

#フォントはMSゴシック
fp_1 = FontProperties(fname='C:\WINDOWS\Fonts\msgothic.ttc', size = 16)

#指数関数のパラメータ
k = 0.14
A = 0.03

#感染源候補者の範囲
kansen_days = 28
td = timedelta(days=kansen_days+1)

で、いよいよデータ読込みと日次集計です。

#東京都の感染者データ読込み
df = pd.read_csv("https://stopcovid19.metro.tokyo.lg.jp/data/130001_tokyo_covid19_patients.csv")
df = df[['公表_年月日']]

#日次集計
df['count'] = 1
df = df.groupby('公表_年月日').agg({'count': np.sum})
df = df.reset_index()
start_at, end_at = df.公表_年月日.min(), df.公表_年月日.max()
df.index = df.公表_年月日

(3) データの解析

「感染源候補者数」を算出し、その日毎の増分も計算します。
さらに前者で後者を割って$k$の値も算出します。
これらを1枚のデータフレームにまとめます。

#感染源候補者数算出
start_at = datetime.datetime.strptime(start_at, '%Y-%m-%d')
dates_DF = pd.DataFrame(index=pd.date_range(start_at-td, end_at, freq="D"))
df = df.merge(dates_DF, how="outer", left_index=True, right_index=True)
df = pd.DataFrame(df['count'].fillna(0).astype(int))
df2 = pd.DataFrame(df.rolling(kansen_days+1).sum().fillna(0).astype(int))
df2 = df2.rename(columns={'count': '感染源候補者数'})

#1つのDataFrameにまとめる
res = df.merge(df2, how="outer", left_index=True, right_index=True)
res = res.rename(columns={'count': '感染者公表数'})
res = res[start_at:end_at]
res['感染源候補者数'] = res['感染源候補者数'] - res['感染者公表数'] 
res['感染源候補者数の増分'] = res['感染源候補者数'].diff().fillna(0).astype(int)
res['k'] = res['感染源候補者数の増分'] / res['感染源候補者数']

比較のために指数関数の値も計算しておきましょう。

#指数関数の値を計算
serial_num = pd.RangeIndex(start=1, stop=len(res.index) + 1, step=1)
res['No'] = serial_num
f = lambda x: (A * math.exp(k*x))
res['Aexpkx'] = res['No'].apply(f)

最後にグラフを描きましょう。

# 描画
fig = plt.figure(figsize=(12, 8))
plt.subplots_adjust(wspace=0.5, hspace=0.9)

ax1 = fig.add_subplot(2, 2, 1)
ax2 = fig.add_subplot(2, 2, 2)
ax3 = fig.add_subplot(2, 2, 3)
ax4 = fig.add_subplot(2, 2, 4)

ax1.plot(res['感染者公表数'])
ax2.plot(res['感染源候補者数'])
ax3.plot(res['k'])

ax4.plot(res['感染源候補者数'])
ax4.plot(res['Aexpkx'])
# 軸目盛の設定
ax1.xaxis.set_major_locator(mdates.WeekdayLocator(byweekday=mdates.SU, tz=None))
ax1.xaxis.set_major_formatter(mdates.DateFormatter("%Y-%m-%d"))
ax1.set_title('感染者公表数', fontproperties = fp_1)
ax1.grid()
ax2.xaxis.set_major_locator(mdates.WeekdayLocator(byweekday=mdates.SU, tz=None))
ax2.xaxis.set_major_formatter(mdates.DateFormatter("%Y-%m-%d"))
ax2.set_title('感染源候補者数', fontproperties = fp_1)
ax2.grid()
ax3.xaxis.set_major_locator(mdates.WeekdayLocator(byweekday=mdates.SU, tz=None))
ax3.xaxis.set_major_formatter(mdates.DateFormatter("%Y-%m-%d"))
ax3.set_title('k(1日当たり感染源候補者を何人増やすか)', fontproperties = fp_1)
ax3.grid()
ax4.xaxis.set_major_locator(mdates.WeekdayLocator(byweekday=mdates.SU, tz=None))
ax4.xaxis.set_major_formatter(mdates.DateFormatter("%Y-%m-%d"))
ax4.set_title('y=A・exp(kt)', fontproperties = fp_1)
ax4.grid()

# 軸目盛ラベルの回転
labels1 = ax1.get_xticklabels()
labels2 = ax2.get_xticklabels()
labels3 = ax3.get_xticklabels()
labels4 = ax4.get_xticklabels()
plt.setp(labels1, rotation=45, fontsize=10);
plt.setp(labels2, rotation=45, fontsize=10);
plt.setp(labels3, rotation=45, fontsize=10);
plt.setp(labels4, rotation=45, fontsize=10);

(4) 結果

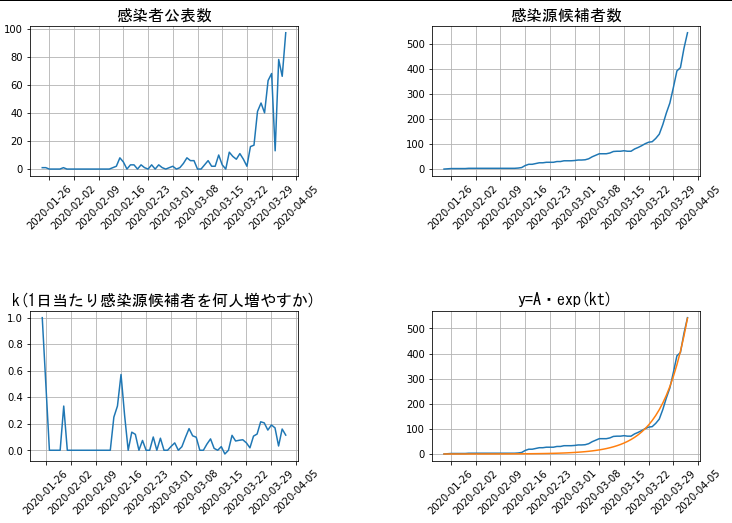
このプログラムを走らせますと、次のようなグラフが得られます。

左上のグラフはニュースなんかでもよく見かけるグラフでしょう。右上は上記の仮定から算出した「感染源候補者数」。上の２つのグラフをいくら眺めていても、現在の施策がうまく行っているのかどうかわからないと思います。
そこで左下の$\kappa$のグラフに注目ください。これが$0.1$あたりをうろうろしているのは恐ろしいことです。実際$A = 0.03,\; \kappa = 0.14$にして

N=A e^{\kappa t}

のグラフを描いてみると、右下のグラフになります。縦軸が「感染源候補者数」、オレンジ線が指数関数モデルで計算した値、ブルー線が実測値です。きわめて単純な仮定に基づいて計算したにもかかわらず、けっこうよく適合しているのではないでしょうか。

(5) 考察

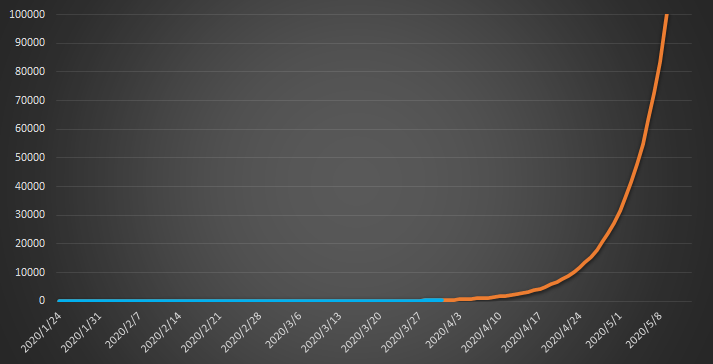
さて、この$A = 0.03,\; \kappa = 0.14$を使って

N=A e^{\kappa t}

のモデルで今後を予測してみましょう。怖いことになっています。

　　　　　　　 　「感染源候補者数」予測値

5月の連休明けには東京都の「感染源候補者数」は10万人を突破します。
もちろん、皆さんの努力で、今後はこのモデルの予測を下回ることは大いに期待できます。
今後打ち出される様々な施策が果たして功を奏しているのか、あるいは焼け石に水なのかはどうすればわかるでしょうか？
そう左下のグラフです。
皆さん、毎日このプログラムを走らせて、この左下のグラフが$0$に向かっているかを確認してください。 もし期待に反してこれが上に向かっているようでしたら大変です。

link

「数週間後の日本の姿？イタリアの新型コロナウィルス感染者数を免疫も考慮したモデルで解析してみた」を新たに投稿いたしました。あわせてお読みいただけると幸いです。