数週間後の日本の姿？イタリアの新型コロナウィルス感染者数を免疫も考慮したモデルで解析してみた

##はじめに
　新型コロナウィルスでイタリアが大変な状況です。イタリアと言えばガリレオ・ガリレイ。「自然という書物は数字の言葉で書かれている」と言ったそうです。私の頭の中も数学の言葉で書かれておりますので、イタリアの状況を数学で記述してみたいと思います。

環境: Windows10 Pro 64bit + anaconda + Python 3.7.3

##(1) 基本式
　「東京での感染爆発をざっくり予測する」というほんの小学校の算数みたいなものを使って導出した回帰式がけっこういろいろな示唆に富んでいて驚愕の帰結をもたらすことを先日投稿させていただきました。ざっと復習すると、
$N(t)$：便宜的に「感染源候補者数」と呼ぶ。第$t$日の直前$n$日間に陽性と報告された人数
$n$：感染力を持ち始めてから失うまでの日数
として「感染源候補者数」の1日当たりの増分が、その日の「感染源候補者数」に比例するとして微分方程式を立てると、

\frac{dN(t)}{dt}=k N(t)

となります。これで東京の今日までのデータを解析したのが前回の投稿でした。
　今回は今すでに大変な状況になっているイタリアのデータを解析します。イタリアでは罹患人数が100万人を超え、免疫保持者も相当な人数になっていることが予想されますので、これも考慮することにしましょう。
$N_c (t)$：第$t$日に陽性と報告された累計人数
として上式に免疫による効果を組み込むと、全人口に占める免疫保持者の割合は$N_c$に比例すると仮定すれば、

\frac{dN(t)}{dt}=k (1-hN_c (t))N(t)

と書けます。解析的に解けないこともないでしょうがここは無精して差分化して数値積分します。すなわち、初期値$N(0)$を決めておいて、

N(t+1)=N(t)+k (1-hN_c(t))N(t)

から、逐次$N$の値を求めていきます。

##(2) データの解析

　すでにKaggleでも新型コロナウィルス関連のコンペが始まっていて整形されたデータが転がってます。今回は
https://www.kaggle.com/sudalairajkumar/novel-corona-virus-2019-dataset
から
time_series_covid_19_confirmed.csv
というデータを拝借し、イタリアの行を抜き出して

公表_年月日	count
2020/1/22	0
2020/1/23	0
2020/1/24	0
2020/1/25	0
2020/1/26	0
:	:
2020/4/2	115242
2020/4/3	119827

と整形します。
今回はこれを上記の数学モデルで解析しましょう。
まずはimport。

import pandas as pd
import matplotlib.pyplot as plt
import random
from datetime import timedelta
import datetime
import matplotlib.dates as mdates
from matplotlib.font_manager import FontProperties
import codecs

次に、さまざまな設定値を書き込みます。回帰式のパラメータを最適化するために実数値GAを使うのでそのパラメータも決めます。

#設定値
fp_1 = FontProperties(fname='C:\WINDOWS\Fonts\msgothic.ttc', size = 16) #グラフ用フォント　MSゴシック

# 数学モデル学習用設定値
# A = 0.019, k = 0.15289
parm_max = [1.8, 0.23, .000001] # パラメータ上界 [Amax , kmax]
parm_min = [0.9, 0.15, .000000001] # パラメータ下界 [Amin , kmin]
kansen_days = 28 #感染源候補者が陽性判定を受けた期間
kaiki_days = 14 #回帰で使うデータの期間
td = timedelta(days=kansen_days+1)
meneki = 1 # 0:免疫考慮せず　1:免疫考慮

# GAパラメータ
gene_length = len(parm_max) # 遺伝子長
individual_length = 20 # 個体数
generation = 10 # 世代数
BLXalp = 1.2 # BLX-α交叉の係数α
mutate_rate = 0.2 # 突然変異の確率
error_thrshd = 7.9e-05 # 最良個体の誤差がこれを下回ったら終了

今回は実数値GAの説明は本題からそれるので割愛します。20年ほど前に大自然を相手にデータ解析をしていて、必要に迫られて数学モデル万能最適化アルゴリズムを作って以来こいつを使い回しています。とても便利なんでいずれどこかで解説しますね。
さて、関数を少し定義しておきましょう。何の関数かはコメントをご参考にしてください。

def init_indiv(): # 初期化した個体を生成する関数 
    parm = []
    for j in range(gene_length):
        parm_new = parm_min[j] + (parm_max[j] - parm_min[j]) * random.random() 
        parm.append(parm_new)
    return parm
def make_DF(): # 解析用DataFrame作成
    #イタリアの感染者データ読込み
    with codecs.open("./Italy/time_series_covid_19_confirmed_Italy.csv", "r", "Shift-JIS", "ignore") as file:
        df = pd.read_table(file, delimiter=",")
    
    df = df.reset_index()
    start_at, end_at = df.公表_年月日.min(), df.公表_年月日.max()
    df.index = df.公表_年月日
    #感染源候補者算出
    start_at = datetime.datetime.strptime(start_at, '%Y-%m-%d')
    dates_DF = pd.DataFrame(index=pd.date_range(start_at-td, end_at, freq="D"))
    df = df.merge(dates_DF, how="outer", left_index=True, right_index=True)
    df = pd.DataFrame(df['count'].fillna(0).astype(int))
    df2 = pd.DataFrame(df.rolling(kansen_days+1).sum().fillna(0).astype(int))
    df2 = df2.rename(columns={'count': '感染源候補者数'})
    covid19_DF = df.merge(df2, how="outer", left_index=True, right_index=True)
    covid19_DF = covid19_DF.rename(columns={'count': '感染者公表数'})
    covid19_DF = covid19_DF[start_at:end_at]
    covid19_DF['感染源候補者数'] = (covid19_DF['感染源候補者数'] - covid19_DF['感染者公表数'] ).astype("int64")
    covid19_DF['感染源候補者数の増分'] = covid19_DF['感染源候補者数'].diff().fillna(0).astype("int64")
    covid19_DF['感染者公表数累計'] = covid19_DF['感染者公表数'].cumsum().astype("int64")
    covid19_DF['k'] = covid19_DF['感染源候補者数の増分'] / covid19_DF['感染源候補者数']
    return covid19_DF

def mathModel(math_DF, A, k, h): #予測値を計算
    math_DF['感染源候補者数'] = math_DF['感染源候補者数'].astype(float)
    math_DF['感染源候補者数予測値'] = math_DF['感染源候補者数']
    for i in range(len(math_DF['感染源候補者数'])-1):
        math_DF['感染源候補者数予測値'][i+1] = math_DF['感染源候補者数予測値'][i] + k * (1 - h * covid19_DF['感染者公表数累計'][i]) * math_DF['感染源候補者数'][i]
    math_DF['SQerror'] = ((math_DF['感染源候補者数予測値'] - math_DF['感染源候補者数']) / (kaiki_days*(math_DF['感染源候補者数']+1))) ** 2
    return math_DF

make_DFという関数はもう少しきれいに書けるでしょうが勘弁してください。普段こういうpandasなやつは梅ちゃん（@T_Umezaki）という優秀な技術者殿に書いてもらっちゃうんで…
それで、肝心なところは下記のところです。

    for i in range(len(math_DF['感染源候補者数'])-1):
        math_DF['感染源候補者数予測値'][i+1] = math_DF['感染源候補者数予測値'][i] + k * (1 - h * covid19_DF['感染者公表数累計'][i]) * math_DF['感染源候補者数'][i]
    math_DF['SQerror'] = ((math_DF['感染源候補者数予測値'] - math_DF['感染源候補者数']) / (kaiki_days*(math_DF['感染源候補者数']+1))) ** 2

ここでは微分方程式を差分化した式を使い逐次計算をしていき、最後まで計算したところで誤差関数値の計算をします。
さて、いよいよメインプログラム。
実数値GAを使って誤差関数値が最小になるように$A$、$k$、$h$を最適化します。

covid19_DF = make_DF()

# 初期個体群生成-------------------------------------
population = []  # 個体群を入れるプール

for i in range(individual_length):
    parm = init_indiv()
    population.append(parm)

# 進化-----------------------------------------------
error_min_list = [] #各世代における誤差の最小値をリスト化
index_min = 1
for g in range(generation):
    population_child = [] # 次世代の個体群を入れるプール

    # 誤差評価------------------------
    error_Sum_All = 0 # 全個体の誤差
    error_indiv = [] # 個体ごとの誤差、その個体の遺伝子配列
    error_max = 0 #　誤差の最大値
    error_min = 10000000000000000 #　誤差の最小値
    for igen in range(individual_length):
        A = population[igen][0]
        k = population[igen][1]
        h = population[igen][2] * meneki
        math_DF = mathModel(covid19_DF, A, k, h)
        error_eval = math_DF['SQerror'][-kaiki_days-1:].sum()
        if error_eval > error_max:
            error_max = error_eval
            
        if error_eval < error_min:
            error_min = error_eval
            index_min = igen
            
        error_indiv.append([error_eval, population[igen]])
        error_Sum_All += error_eval   
        
    error_min_list.append([g, error_min])
    print('Generation: ' + str(g))
    print(' ###### best gene Id : ' + str(index_min))
    print(' ###### Error_min: ' + str(error_min))
    print(' ###### best gene: ' + str(population[index_min]))
        
    if error_min < error_thrshd:
        break
        
    error_indiv_sum = 0  # 最大誤差-個体ごとの誤差　の合計  
    for i in range(individual_length):
        error_indiv[i][0] = error_max - error_indiv[i][0] # 最大誤差-個体ごとの誤差
        error_indiv_sum += error_indiv[i][0]
        
    for i in range(int(individual_length/2)):
        error_cum1 = 0 # 最大誤差-個体ごとの誤差　の累計
        error_cum2 = 0
        i_parent1 = 0
        i_parent2 = 0

    # 親選び
        r_parent1 = random.random() * error_indiv_sum
        r_parent2 = random.random() * error_indiv_sum
        for j in range(individual_length-1):
            error_cum1 += error_indiv[j][0]
            error_cum2 = error_cum1 + error_indiv[j+1][0]
            if (error_cum1 <= r_parent1) and (error_cum2 >= r_parent1):
                i_parent1 = j + 1
            if (error_cum1 <= r_parent2) and (error_cum2 >= r_parent2):
                i_parent2 = j + 1
                
    # 交叉(BLX-α)
        child1 = [] # 子供1
        child2 = [] # 子供2
        
        for j in range(gene_length):
            prt_gene1 = population[i_parent1][j]
            prt_gene2 = population[i_parent2][j]
            cld_gene1 = (prt_gene1 + prt_gene2) / 2 \
            + (random.random()-0.5) \
            * abs(prt_gene1 - prt_gene2) * BLXalp
            
            cld_gene2 = (prt_gene1 + prt_gene2) / 2  \
                + (random.random()-0.5) \
                * abs(prt_gene1 - prt_gene2) * BLXalp
            child1.append(cld_gene1)
            child2.append(cld_gene2)
        population_child.append(child1)
        population_child.append(child2)
    
    # 突然変異
        for j in range(int(mutate_rate*individual_length)):
            mut_indiv = random.randrange(individual_length)
            population[mut_indiv] = init_indiv()

    # 個体群世代交代
    population = population_child
         
# 最良個体の解析結果を出力
igen = index_min
A = population[index_min][0]
k = population[index_min][1]
h = population[index_min][2] * meneki
math_DF_min = mathModel(covid19_DF, A, k, h)

print(' best gene Id : ' + str(index_min))
print(' A=', population[index_min][0])    
print(' k=', population[index_min][1])  
print(' h=', population[index_min][2])

実数値GAのコードがうるさいと思います。最適化のライブラリは一切使わないのが老技術者の意地なんでございます。

##(3) 結果
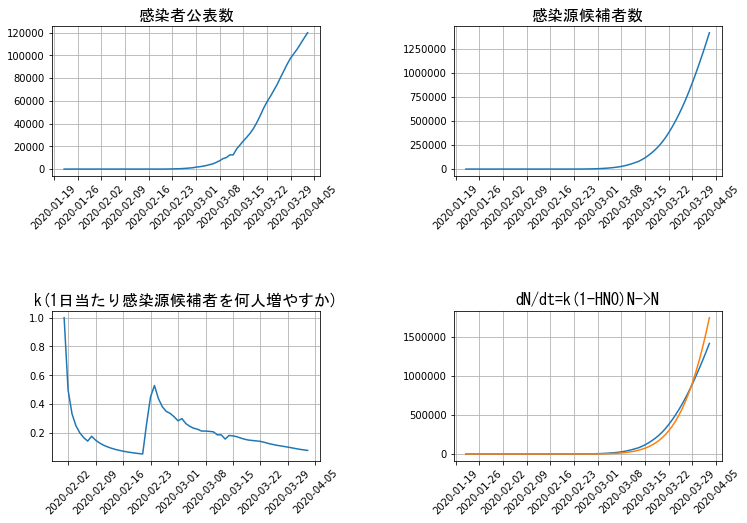
　このモデルを使ってイタリアの「感染源候補者数」の時系列データをシミュレーションした結果を見てみましょう。まず、meneki = 0、すなわち免疫の効果なしでプログラムを走らせると、

               図1 イタリア（免疫効果なし）

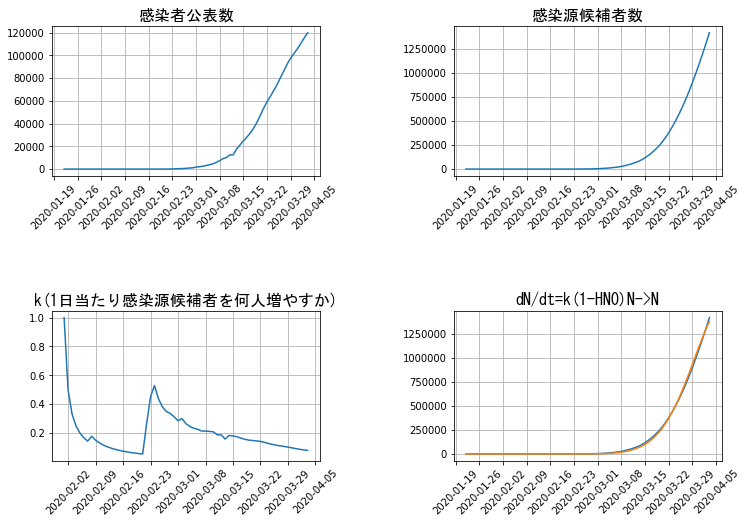
となります。図1右下のグラフを見るとブルー線の実測値がオレンジ線の予測値（指数関数）の下にブレつつあります。そこで、meneki = 1、すなわち免疫の効果ありでプログラムを走らせると、

               図2 イタリア（免疫効果あり）

図2では右下のブルー線とオレンジ線はピタリと重なりました。上記の仮定通り免疫の効果が出ている可能性が示唆されました。
注目すべきは、左下のグラフ。「東京での感染爆発をざっくり予測する」に載せたグラフで$k$が0.1から0.2の間を何となく上昇している図3の日本の場合と比較してみましょう。

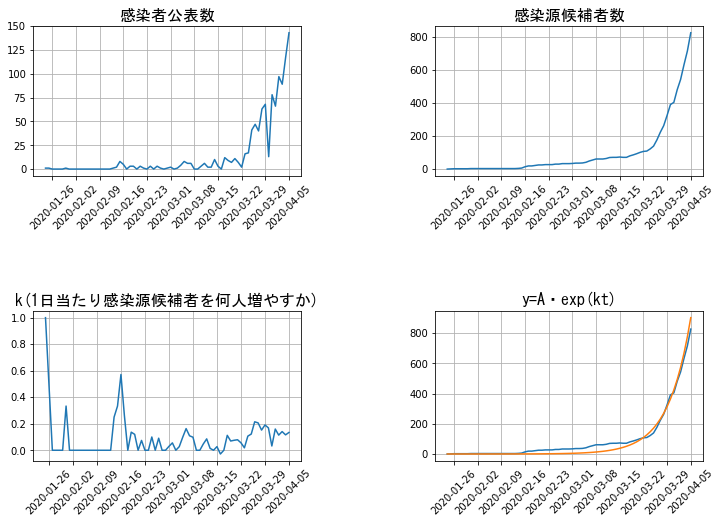
               図3 東京（免疫効果なし）

　$k$の値は「感染源候補者数」を増やすアクセルの踏み具合のようなもので、もちろん大きいほどヤバいわけです。イタリアの場合、2月下旬のヤバさが数字で表れてきた直後からほぼ単調に減少しています。何らかの施策が功を奏したと考えられます。

k = \frac{\frac{dN(t)}{dt}}{N(t)}

で$k$を計算していますので、最近では免疫保持者数の増加による効果も加わっているはずです。
　一方、日本の場合は振動しながらもじわじわと$k$が上昇しているのがわかります。これが下降していかない限り、「感染源候補者数」は指数関数に乗って増加していきます。指数関数というのは2倍になるのにかかる時間が一定というおそろしい増加関数です。
　とりあえず、早めに皆さんに解析結果をお見せしたかったので、細かい記述はせず公開します。