Polarsで効果検証入門 第１章のデータ集計と有意差検定をやってみた

はじめに

今回は効果検証入門の学習とPolarsの学びを兼ねて、Rで書かれたコードをPythonのPolarsを使って再現してみました。
乱数を使用していることから、書籍と異なっている部分がありますがご了承ください。
コードが間違っている場合にはご指摘いただけますと幸いです。

目次

1. RCTデータの集計と有意差検定
2. バイアスのあるデータによる検証
3. 参考文献

RCTデータの集計と有意差検定

データの作成

データセットはThe MineThatData E-Mail Analytics And Data Mining Challengeのメールマーケティングデータを使用しています。

# データの読込
import pandas as pd
import polars as pl
data = pd.read_csv("http://www.minethatdata.com/Kevin_Hillstrom_MineThatData_E-MailAnalytics_DataMiningChallenge_2008.03.20.csv")
#なぜかpl.read_csvをするとspendを正しく読み込めない
data = pl.from_pandas(reserve_tb.reset_index())

1. segmentカラムのWomens E-Mailを除去し、女性向けメールを除いたデータセットを作成（男性向けとメール配信なしのグループに絞る）

2. 介入（メールの配信）の示すフラグを立てる
   (treatment：Mens E-Mail = 1、配信なし＝0)

data.with_columns(
    pl.when(pl.col("segment") == "Mens E-Mail")
    .then(1)
    .otherwise(0)
    .alias("treatment")
)

有意差検定

介入ありとなしのそれぞれのグループで、購入の発生確率(conversion)と購入金額(spend)の平均を計算

male_df = data.filter(
    pl.col('segment') != 'Womens E-Mail'
)

male_d.with_columns(
    pl.when(pl.col("segment") == "Mens E-Mail")
    .then(1)
    .otherwise(0)
    .alias("treatment")
    ).groupby('treatment').agg(
        pl.col('conversion').mean(),
        pl.col('spend').mean()
)

出力結果

Polarsならこんな処理も一気に…

次に、介入グループ（男性向けメールが配信）の購買データと、非介入（メール配信なし）グループの購買データで有意差検定（２群間の平均の差でt検定）

# 男性向けメールが配信されたグループ
mens_mail_df = male_df.filter(
        pl.col('treatment') == 1,
        ).select(
        pl.col('spend')
    )
# メール配信なしのグループ
no_mail_df = male_df.filter(
    pl.col('treatment') == 0
    ).select(
    pl.col('spend')
)

# ２群間のt検定
# 平均の差に対して有意差検定を実行
from scipy import stats
stats.ttest_ind(mens_mail_df, no_mail_df, equal_var=True)

出力：Ttest_indResult(statistic=array([5.30009029]), pvalue=array([1.16320087e-07]))

p値は1.16e-07と非常に小さいため統計的に有意

バイアスのあるデータによる効果の検証

バイアスをつけたデータの準備

1. 介入データ側から購入意欲の小さい人をランダムで除く
2. 非介入データからは購入意欲の高い人をランダムで除く

という処理を行い、無理やりバイアスを擬似的に作成
具体的には

「去年の購入額であるhistoryが300より大きい場合」,
「最後の購入であるrecencyが6より小さい場合」,
「接触チャネル channelが複数あることを表すMultichannelである場合」のOR条件を満たす人を意欲的と判断する。

# データを複製
bias_df = male_df.__copy__()

# メールが配信されていないグループ
# ランダムで50%を抽出
no_mail_del_df = bias_df.select(
    bias_df.filter(pl.col('treatment') == 0)
    .filter((pl.col('history') > 300) | (pl.col('recency') < 6) | (pl.col('channel') == 'Multichannel'))
).sample(fraction=0.5, seed=1)

# 抽出したユーザーを削除
no_mail_bias_df = bias_df.select(
    bias_df.filter(
        ~pl.col('index').is_in(no_mail_del_df['index'])
    )    
)

# メールが配信されているグループ
male_mail_del_df = bias_df.select(
    bias_df.filter(pl.col('treatment') == 1)
    .filter((pl.col('history') <= 300) & (pl.col('recency') >= 6) & (pl.col('channel') != 'Multichannel'))
).sample(fraction=0.5, seed=1)

# 抽出したユーザーをさらに削除
male_mail_bias_df = no_mail_bias_df.select(
    no_mail_bias_df.filter(
        ~pl.col('index').is_in(male_mail_del_df['index'])
    )
)

有意差検定

バイアスをつけた群間の検定を先ほどと同様に行います。
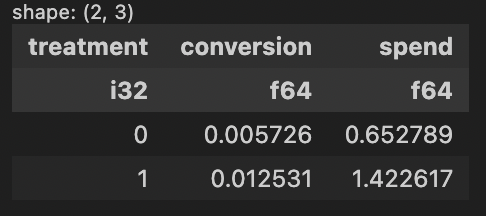
まずは、グループ毎にconversionとspendの平均を算出

# バイアスありのデータの
male_mail_bias_df.groupby('treatment').agg(
        pl.col('conversion').mean(),
        pl.col('spend').mean()
)

出力結果

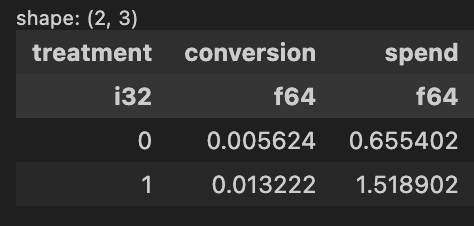
バイアスなしの結果と比較すると、conversionの差が大体0.007→0.008くらい若干広がっています。spendも同様に差が広がっていることが確認できます。
ここで、平均の差についてt検定を行うと

# 男性向けメールが配信されたグループ
mens_mail_df =male_mail_bias_df.filter(
        pl.col('treatment') == 1,
    ).select(
        pl.col('spend')
    )
# メール配信なしのグループ
no_mail_df = male_mail_bias_df.filter(
    pl.col('treatment') == 0
).select(
    pl.col('spend')
)

# ２群間のt検定
# 平均の差に対して有意差検定を実行
from scipy import stats
stats.ttest_ind(mens_mail_df, no_mail_df, equal_var=True)

出力：Ttest_indResult(statistic=array([4.86607937]), pvalue=array([1.14376213e-06]))

p値は非常に小さく、統計的に有意となります。

p値がバイアスかける前よりなぜか大きくなっている…。
どこかでミスをしているか、乱数の影響…。

参考文献

• Polars documentation
• 効果検証入門〜正しい比較のための因果推論/計量経済学の基礎