結論
なんだかんだでpopcountが早い。
Rustのu128にはtrailing_zerosという専用の関数が用意されていました…、多分これが一番早いです。
以下はそれを知らない状態での記事なので、興味がある人以外は、これを使えば良いと思います。
はじめに
ボードゲームをRustで実装している時に、Bitboardを触ることが多くなってきたので、実験結果を記事にまとめておいてあとで見返そうかなと思っています。あくまで参考程度に
実験内容
Rustのu128(128bit符号なし整数)を対象に行っています。
処理内容は以下のように与えられたビット列に対してその右端のビットの位置を返すような関数です。
.#.##(some binary sequence)..#..#.....
^ここ
比較する手法は以下の3つです。
A(Normal実装)
素朴にひとつずつルーブでシフトしながら探す方法。特に言うことはない。
実装は以下のような感じ。
pub fn get_trailing_zeros_normal(bit: u128) -> usize {
for i in 0..128 {
if (bit >> i) & 1 == 1 {
return i as usize;
}
}
return 0;
}
B(pop count)
有名なポップカウントを使った方法。ポップカウントはビットボード上の立ってるビットの数を高速で数え上げるアルゴリズムらしいです。
実装は適当な記事からパクったものです。
pub fn get_trailing_zeros_pop(bit: u128) -> usize {
// 対象のビットより左を全て1にしてから反転させる
let bit = bit | (bit << 1);
let bit = bit | (bit << 2);
let bit = bit | (bit << 4);
let bit = bit | (bit << 8);
let bit = bit | (bit << 16);
let bit = bit | (bit << 32);
let bit = bit | (bit << 64);
// この時点で bit = 1111111..111100000...00
let bit = !bit;
// bit = 000000...000011111...11
// ここからpop count
let bit = bit - ((bit >> 1) & 0x55555555555555555555555555555555);
let bit = (bit & 0x33333333333333333333333333333333)
+ ((bit >> 2) & 0x33333333333333333333333333333333);
let bit = (bit + (bit >> 4)) & 0x0f0f0f0f0f0f0f0f0f0f0f0f0f0f0f0f;
let bit = bit + (bit >> 8);
let bit = bit + (bit >> 16);
let bit = bit + (bit >> 32);
let bit = bit + (bit >> 64);
let idx = bit & 0xff;
return idx as usize;
}
C(特殊なビット列を使った方法)
de Bruijin Sequenceという特殊なビット列を使った方法。
先に実装を見せておきます。
const U128_BRUIJIN_TABLE: [usize; 128] = [
0, 1, 101, 2, 116, 102, 60, 3, 124, 117, 103, 94, 82, 61, 33, 4, 125, 121, 118, 87, 111, 104,
95, 53, 90, 83, 69, 62, 48, 34, 20, 5, 126, 114, 122, 80, 119, 109, 88, 46, 112, 107, 105, 73,
96, 75, 54, 26, 98, 91, 84, 66, 77, 70, 63, 39, 56, 49, 42, 35, 28, 21, 14, 6, 127, 100, 115,
59, 123, 93, 81, 32, 120, 86, 110, 52, 89, 68, 47, 19, 113, 79, 108, 45, 106, 72, 74, 25, 97,
65, 76, 38, 55, 41, 27, 13, 99, 58, 92, 31, 85, 51, 67, 18, 78, 44, 71, 24, 64, 37, 40, 12, 57,
30, 50, 17, 43, 23, 36, 11, 29, 16, 22, 10, 15, 9, 8, 7,
];
const U128_BRUIJIN_MASK: u128 = 0b1111111;
const U128_BRUIJIN_BIT: u128 = 0b1111111011111001111010111100011101101110100111001011100001101100110101011010001100100110001011000001010100101000010010001;
pub fn get_trailing_zeros(bit: u128) -> usize {
let bit = bit & (!bit + 1);
let idx = ((bit.wrapping_mul(U128_BRUIJIN_BIT)) >> 121) & U128_BRUIJIN_MASK;
return U128_BRUIJIN_TABLE[idx as usize];
}
de Bruijin Sequenceについて
この数列は都合の良いある性質を持っています。
例として8bitのものが以下です。
0011101
これはビット列のどの三桁を抜き出しても他とはかぶらない数値になります
00111010
001 [0]
011 [1]
111 [2]
110 [3]
101 [4]
010 [5]
100 [6]
000 [7]
つまり例えば一つだけビットが立っているBitboard(例0001000)を持ってきて、この列と掛け算をすると、何桁かシフトします
00010000 * 00111010 = 001110100000
そしてこれを、5(=1<<3 - 3)だけ右にずらして下三桁をとってきます。
001110100000 >> 5 = 0011101
0011101 & 111 = 101
この101は[4]の位置にあるので、掛け算によって4つ左にシフトしたことがわかります。
これを128bitの拡張したのが今回の方法です。
測定
時間の測定には以下の関数を使用しました
fn bench_get_trailing_zeros() {
let n = 100000u128;
let mut count_n = 0;
let mut count_b = 0;
let mut count_p = 0;
let sum = n * 128;
for _ in 0..n {
for j in 0..128 {
let bit = 1 << j;
count_n += get_time_nanos(|| {
bitboard::get_trailing_zeros_normal(bit);
});
count_b += get_time_nanos(|| {
bitboard::get_trailing_zeros(bit);
});
count_p += get_time_nanos(|| {
bitboard::get_trailing_zeros_pop(bit);
});
}
}
println!("[normal] total:{}ns, {}ns/times", count_n, count_n / sum);
println!("[pop] total:{}ns, {}ns/times", count_p, count_p / sum);
println!("[bruijin] total:{}ns, {}ns/times", count_b, count_b / sum);
}
fn get_time_nanos<F: Fn()>(f: F) -> u128 {
let start = Instant::now();
f();
let end = start.elapsed();
return end.as_nanos();
}
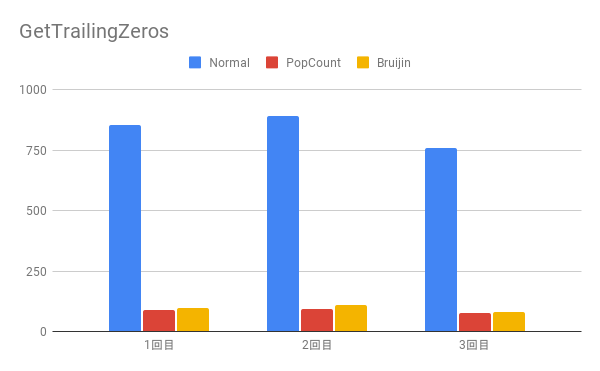
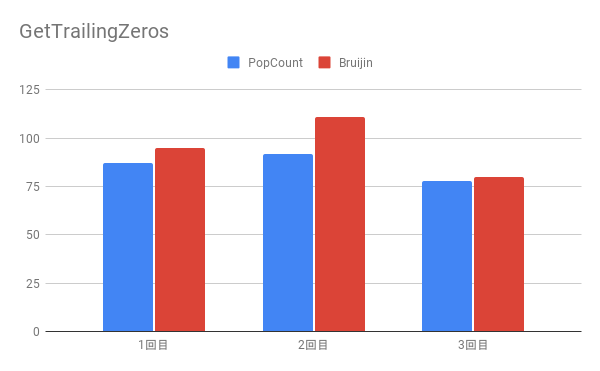
実験結果
1回目
[normal] total:10930887711ns, 853ns/times
[pop] total:1115264850ns, 87ns/times
[bruijin] total:1224275962ns, 95ns/times
2回目
[normal] total:11442418073ns, 893ns/times
[pop] total:1180044299ns, 92ns/times
[bruijin] total:1429340564ns, 111ns/times
3回目
[normal] total:9751323294ns, 761ns/times
[pop] total:1006578278ns, 78ns/times
[bruijin] total:1029734167ns, 80ns/times
グラフ
ポップカウントが一番、Bruijin Sequenceを使った方法が二番、ノーマルが圧倒的に最下位となりました。
上の二つはほとんど変わらない位でしたが、実装の手間を考えると圧倒的にPopCountが良いですね。