回帰分析の評価指標まとめ ～決定係数と紛らわしい相関係数の説明を添えて～

はじめに

回帰分析モデルの評価指標について解説していきます。併せて決定係数と紛らわしい相関係数について解説します。この投稿では特に以下の項目に焦点を当てています。

• 各評価指標の説明
• 各評価指標の使い分けと注意点
• 決定係数と相関係数の関係

※機械学習やプログラミング関係の内容を他にも投稿していますので、よろしければこちらの一覧から他の投稿も見て頂けますと幸いです。

評価指標

回帰分析で得られたモデルの適合の良さを評価する主な指標は以下です。

• 決定係数R²
• 自由度調整済み決定回数
• 平方根平均二乗誤差（RMSE：Root Mean Squared Error）
• 平均二乗誤差（MSE：Mean Squared Error）
• 平均絶対誤差（MAE：Mean Absolute Error）
• 赤池情報量基準（AIC：Akaike's Information Criterion）
• 重相関係数

これらの評価指標について以下で説明していきます。

決定係数R²

R^2=1-\frac{\sum_{i=1}^{n}  (y_i-\hat{y_i})^2}{\sum_{i=1}^{n}  (y_i-\bar{y})^2}\

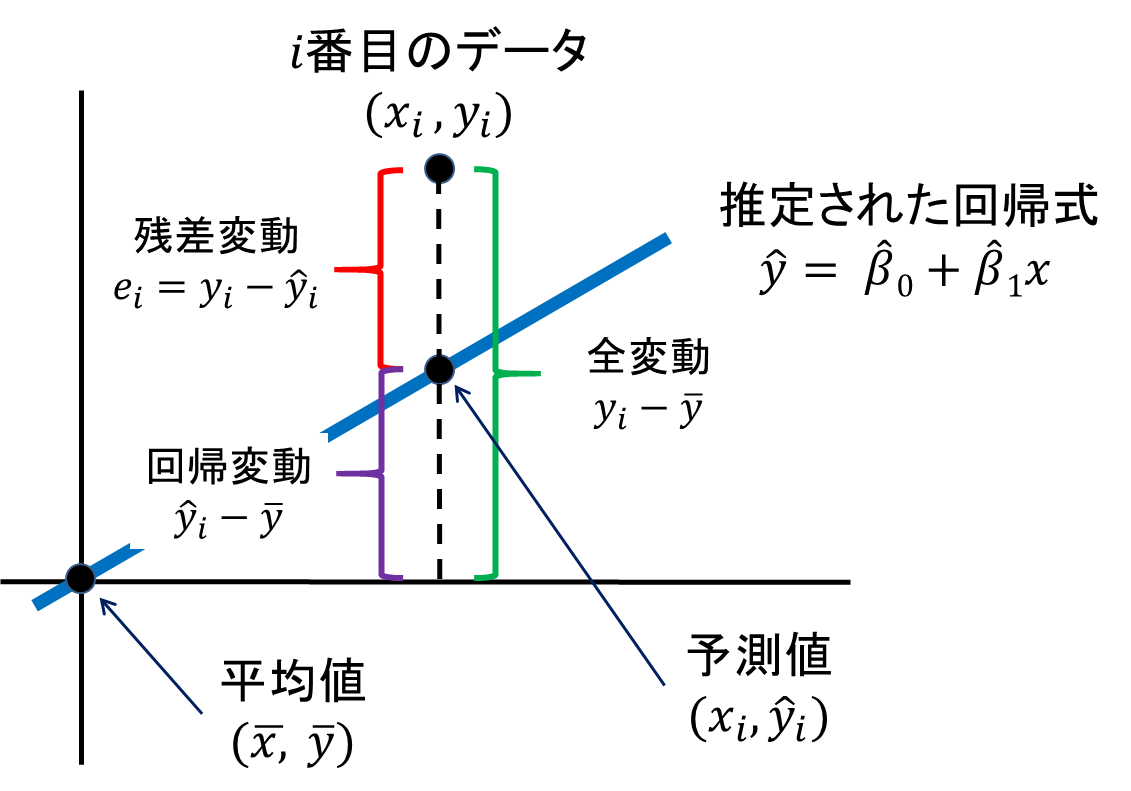
各文字の意味は以下の図を参照ください。こちらを参考にさせていただきました。決定係数を算出する際は1から全変動に対する残差変動の割合を引いており、残差変動が小さいとR²は1に近づき、モデルの予測精度が高いと言えます。

決定係数R²は推定された回帰式の当てはまりの良さ（度合い）を表します。1に近いほど回帰式が実際のデータに当てはまっていることを表します。
※R²とありますが、場合によっては負の値をとることもありえます

自由度調整済み決定係数

決定係数は説明変数の数が増えるほど大きくなるという性質を持っています。ですので、重回帰分析で扱う説明変数の数に応じて決定係数が小さくなるように補正をした値を自由度調整済み決定係数（自由度修正済み決定係数）と言います。（統計検定2級の問題でよく見ました）

平方根平均二乗誤差（RMSE）

RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n}  (y_i-\hat{y_i})^2}

決定係数R²の説明を参照すると、RMSEは残差変動の二乗平均の平方根を表しています。RMSEは0に近いほどモデルの予測精度が高いことを意味します。**外れ値が含まれると、観測値と計算値（予測値）の差が大きく離れるため、RMSE が著しく大きくことから、RMSE は外れ値の影響を受けやすいといわれています。**この性質を生かして大きな誤差を出すサンプルを少なくしたい際にはRMSEを使うことが多いです。

平均二乗誤差（MSE）

MSE=\frac{1}{n}\sum_{i=1}^{n}  (y_i-\hat{y_i})^2

RMSEの平方根がない（RMSEを二乗した）値です。

平均絶対誤差（MAE）

MAE=\frac{1}{n}\sum_{i=1}^{n}  |y_i-\hat{y_i}|

MAEは残差変動の絶対値の和です。MSE(RMSE)と異なり、残差変動をを二乗しないので全サンプルの誤差を平等に評価すると言えます。よって、サンプル全体に対する誤差をなるべく小さくしたい際にはMAEを評価指標に用いることが多いです。

赤池情報量基準（AIC）

AIC=-2(logL-k)

ある統計モデルの最大尤度をLとし、モデルに含まれるパラメーター数をkとします。統計モデルにおいて、モデルの複雑さ適合性能の両方を評価したい場合に用いられます。

重相関係数

実際に観測された目的変数の値と、重回帰式をあてはめて計算した推定値（理論値）との相関係数です。重相関係数は一般にで示され、0から1の間の値を取ります。1に近いほど分析の精度は高いと言えます。

評価指標に関する注意点

• 評価指標は同一のデータセットに対して算出した結果同士のみ比較することができる（Pythonでデータセットを作成する場合はrandom_stateを固定するなどの対応が必要）
• 訓練データとテストデータの両方に対して評価指標を算出する（訓練データとテストデータの両方への適合が必要）
• RMSEおよびMAE はいずれも元のデータと同じ単位を持っており、「見積もられる誤差の大きさ」を表す

相関係数

相関係数rと決定係数R²はたまに混同されるので以下に整理します。（そういう私も以前は相関係数と決定係数があまり分かっていませんでした…）

• 相関係数r：xとyの「相関」を表す。－1に近いと強い負の相関、1に近いと強い正の相関
• 決定係数R²：モデルの「当てはまりの良さ」を表す。予測したyと実際のyとの類似度を表すようなもの

1変数を用いた単回帰分析では相関係数rの二乗が決定係数R²になります。

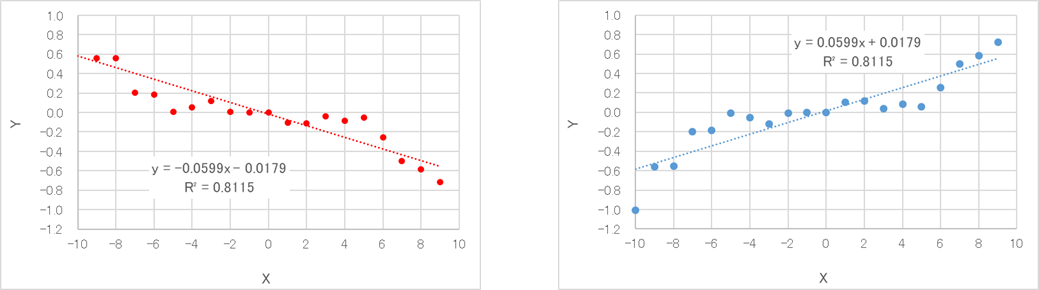
以下のグラフはともに決定係数R²は0.81ですが、相関係数rは左側が-0.90で右側が0.90です。

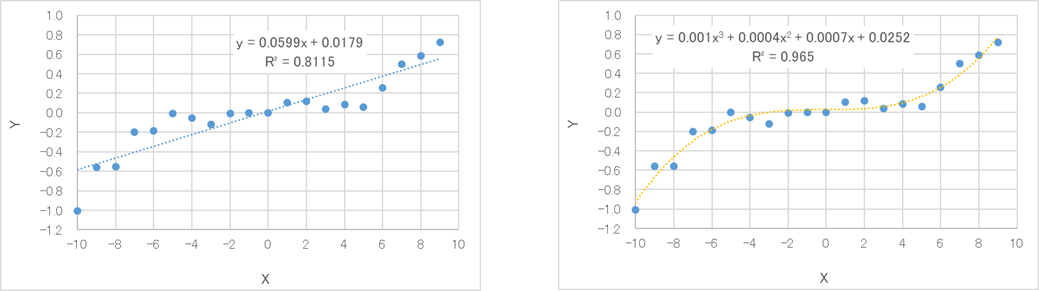
相関係数は2つの変数間の「直線的な」相関を表す値です。ただ、決定係数はモデルの「当てはまりの良さ」を表す値なので、回帰モデルによって値が異なります。以下のグラフは同一のデータを用いており相関係数rはともに0.90ですが、左側が一次関数で近似したモデルで決定係数R²は0.81、右側が三次関数で近似したモデルで決定係数R²は0.97です。

まとめ

回帰分析モデルの評価指標について解説致しました。

• 回帰分析の評価指標はいくつか存在する
• 重要視する項目やモデルの設計方針によって採用する評価指標が異なる
• 決定係数はモデルの「当てはまりの良さ」を表し、相関係数は変数間の「相関」を表す値である

参考

• biostatistics
• 統計WEB
• Instruction of chemoinfomatics