はじめに
統計検定2級のための勉強ノートを紹介します。勉強方法全般についてはこちらを参照下さい。なお、以下の内容は統計WEBの初級編と基礎編をまとめたものです。
勉強ノート
まずは初級編のまとめノートです。基礎的な事項ばかりですね。
次に基礎編です。この内容までマスターできれば統計検定2級はばっちりです。
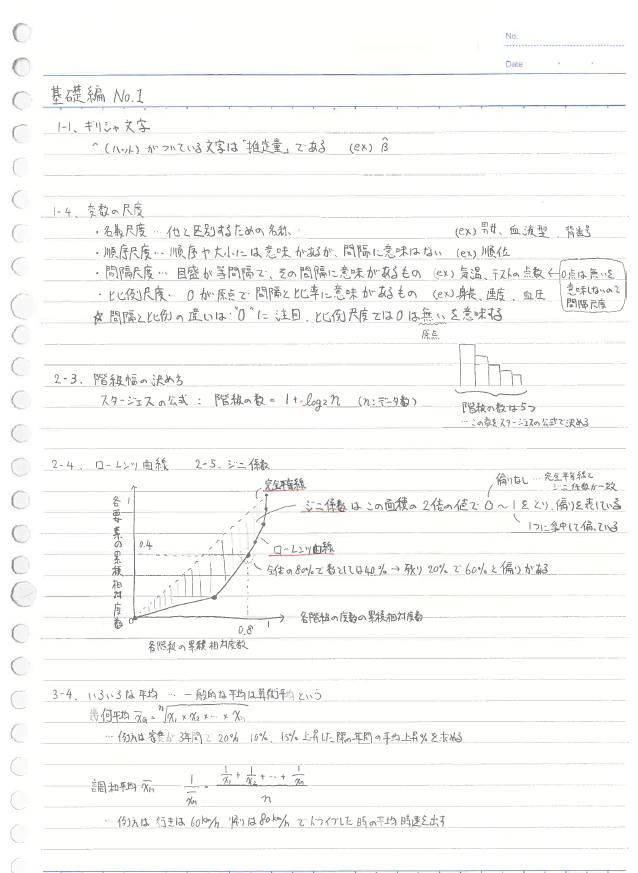
 歪度や尖度は過去問でもたまに出題されています。確実に得点したい内容です。
 最後の分散の公式は重要です。
 「二項分布」、「幾何分布」、後述する「指数分布」の違いはしっかりとおさえたいです。

 「母集団」と「標本」の関係性は重要です。標本の抽出方法も過去問では頻出です。
 ここから出てくる検定量の理解は必須です。
 第1種の過誤や検出力についてもしっかりと理解したい範囲です。

 <追加分>は過去問を解いていて足りなかった知識をまとめています。

 独立性の検定も過去問で出題があり、要注意です。
 一元配置、二元配置の分散分析は確実に得点したい内容です。自由度や自由度やF値の算出も自分の手を動かしてマスターしたいです。
まとめ
統計検定2級の勉強に用いたノートを紹介しました。時間はかかりますが、やはり自分の手を動かしてまとめることで内容の定着度が上がった気がします。

