はじめに

本記事は、「データ構造とアルゴリズム Advent Calendar 2019」 9日目の記事です．
8日目の記事は @goonew 氏による「O(n loglog n)時間で整数をソートする（Word RAM modelを仮定して）」でした．
10日目の記事は @jkr_2255 氏による「フィボナッチ数列を計算する」です．

本記事の概要

本記事では，3進数（即ち3種類の文字で構成される文字列）を簡潔に表現する方法を紹介します．
※ 「前置きはいらないので結論だけ知りたい！」という方は「簡単・実用的・コンパクトな表現方法（方法3）」の章まで飛んでいただいても構いません．

本記事の内容は "Succincter" という論文の内容を参考にしていますので，理論的な詳細について知りたい方は元論文¹をご参照ください．

計算モデルや配列添字の仮定

本記事は，入力サイズ $N$ に対してワードサイズが $w \in \Theta(\log N)$ bits である word RAM モデルを仮定して話を進めていきます．「word RAM って何？専門用語よくわからん！」って人は，$w$ は int 型の変数１個分のビット長 ($w = 32$ とか $w = 64$) だと思って読み進んでいただければ，ほとんどokだと思います．

なお，word RAM のしっかりとした定義は本アドベントカレンダー8日目の記事に書かれているので，word RAM をご存じない方は是非ともそちらをご覧ください．

また，本記事における文字列および配列の添字は，0番目から始まるものとします．

3進数をビット表現しよう

ここでは例として，15桁の3進数 $t = 202021100102120$ をビット列に符号化する3つの方法を考えてみます（例の検証にはこちらのツールを利用させていただきました）．

(方法 1) $t$ を単純に数値として扱い，2進数に変換
3進数 $t$ を10進数に変換すると，10,773,474 という値になります．
よって，$t$ の2進数表現 $t'$ は $t' = \mathtt{1010 0100 0110 0011 1110 0010}$ となります．24 bits になりました．

(方法 2) $t$ の各桁を2進数に変換
$t$ に以下のような変換を噛ませたビット列を $t''$ としましょう．
$\mathtt{0} \rightarrow \mathtt{00}$, $\mathtt{1}\rightarrow \mathtt{01}$, $\mathtt{2}\rightarrow \mathtt{10}$
すると $t''$ は，$t'' = \mathtt{10 00 10 00 10 01 01 00 00 01 00 10 01 10 00}$ となります．30 bits になりました．

(方法 3) 5桁の3進数を8桁の2進数に変換（詳細は後述）
詳細は後述しますが，この符号化を用いると $t$ を $\mathtt{10110110 01010101 01000101}$ という24 bits で表現することができます．

以上の3つの手法を眺めてみると，表現サイズの面では方法1,3がいい感じで，方法2はイマイチに見えます．実際に，表現サイズの大小関係は一般には以下のようになります．
$$
(方法1) \le (方法3) \le (方法2)
$$

サイズとしては方法1の表現が最適なのですが，この表現には1つ欠点があります．
それは，元の3進数の特定の桁を定数時間で計算することができないという点です．

もちろん，元の3進数をすべて復元してあげれば任意の桁に素早くアクセスできます．しかし，「元の3進数を復元」という操作は定数時間では実行できません．これはあまり嬉しくない状況です（嬉しくない）．

一方で，方法2の表現に関しては「2 bits の塊が元の3進数の1桁に対応する」とわかっているため，任意の桁に定数時間でアクセスできます（嬉しい）．ただし表現サイズは最適ではありません（嬉しくない）．

そこで，方法3です．
詳細をまだ説明していないのでイメージが全く湧かないと思いますが...
結論だけを言うと，この表現は"ほぼ最適なサイズ"（嬉しい！）であり，かつ"任意の桁に定数時間でアクセスが可能"（嬉しい！！）という素晴らしい表現となっています．

各方法の特徴を次の表にまとめておきます．ここで $N$ は入力3進数列の長さとします．

	表現のサイズ	各桁への定数時間アクセスが可能か？
方法1	$\lceil (\log_2{3})N\rceil$ bits	No
方法2	$2N$ bits	Yes
方法3	$1.6N$ bits²	Yes

ちなみに，$\log_2{3}$ はおよそ 1.585 です．
方法1は最適サイズ³であり，方法3は最適サイズにかなり近いことがわかると思います．

さて，ここからは方法3について具体的に見ていきましょう．

簡単・実用的・コンパクトな表現方法（方法3）

以下，3進数の各桁を trit と呼ぶことにします．

5 trits を 8 bits に変換

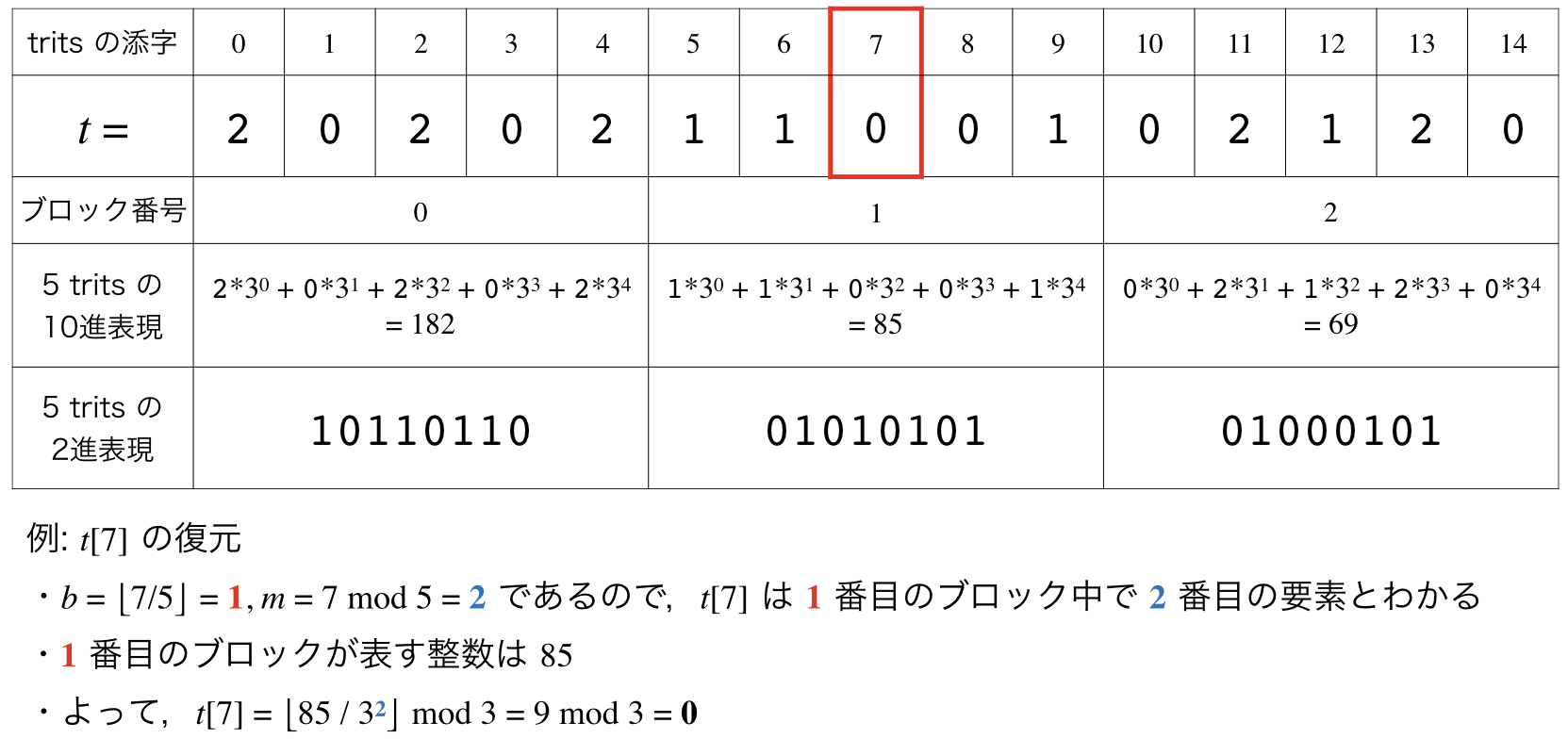
(方法3)のアイデアはとてもシンプルで，$5$ trits を $8$ bits に変換するだけです．ただし，ここでは各 $5$ trits の中では左の桁が下位桁であるとしましょう．また，簡単のため $N$ は5の倍数であるとして考えてみます(図1に具体例を示します):

入力 $t$ を $5$ trits ずつの $N/5$ 個のブロックに分割する．
各ブロックの $5$ trits ($ = abcde$) に対して，
1. $x = a \cdot 3^{0} + b \cdot 3^{1} + c \cdot 3^{2} + d \cdot 3^{3} + e \cdot 3^{4}$ を計算する．
2. $x$ を $8$ bits で保存する ($3^5 < 2^8$ であるので，これは常に可能です)．
$8$ bits $\times$ $N/5$ ブロックで，合計 $1.6N$ bits の表現が得られる．

簡単ですね！この符号化アルゴリズムは入力サイズ $N$ に対して線形な時間で動作します．

[図1. 符号化と復号の例]

また，$t$ の $i$ 番目の要素 $t[i]$ へのアクセスは，以下の通り実現できます(こちらも図1に具体例を示します):

$b = \lfloor i/5 \rfloor$, $m = i~\text{mod}~5$ とする
$b$ 番目のブロックを10進数 $y$ とみなす
すると $t[i] = \lfloor y / 3^{i}\rfloor~\text{mod}~3$ である

これまた簡単ですね！この復号アルゴリズムは定数時間⁴で動作します．

実装

@kampersanda 氏による実装が公開されています⁵．
こちらの実装では，符号化と復号だけでなく，trits 上での rank/select クエリもサポートされています．

README のサンプルを参考に，手元で minimal なコードを書いて動かしてみました．

test.cpp

#include <iostream>
#include <trit_vector.hpp>

int main() {
    std::vector<uint8_t> trits = {2, 0, 2, 0, 2, 1, 1, 0, 0, 1, 0, 2, 1, 2, 0}; 
    succinctrits::trit_vector tv(trits.begin(), trits.size());
    int i = 7;
    std::cout << "t[" << i << "] = " << uint32_t(tv[i]) << std::endl;
    return 0;
}

実行例(ここではリポジトリをホームディレクトリ直下に clone しています):

$ g++ -std=c++11 -I$HOME/succinctrits/include test.cpp 
$ ./a.out
t[7] = 0

いい感じです．
詳細は README をご参照ください．

理論的なお話

ここからは一部のマニアックな方のために，理論的な話を少しだけしたいと思います．
"Succincter" では spill-over encoding というシンプルな符号化手法が提案されました．まずはその spill-over encoding を紹介していきます．

Spill-over Encoding

ここでは，任意の集合 $X$ 中の任意の要素 $x$ をビットで符号化することを考えます．
もちろん，最適表現のビット数は $\lceil\log_2{|X|}\rceil$ bits です．

Spill-over encoding では，ある適切なパラメータ $M$ を設定し，$x$ を $2^M$ で割った余りと商で分割します．
例えば， $X = \{0, 1, 2, \cdots, 242\}$ のとき， $M = 6$ と設定したとしましょう．
そして $x = 182 \in X$ を上記のルールで分割することを考えます．
すると，$182 = 2 * 2^6 + 54$ であるので，余り $54$ と商 $2$ に分割できます（このときの商を spill と呼んでいます）．
したがって，それらをビット表現すると，$\mathtt{110110}|\mathtt{10}$ となります（わかりやすさのために，余りと商の区切り位置に | を引いています）．前半の $M = 6$ bits が余りを表し，残りの 2 bits が商を表しています．

Spill-over encoding は復号操作も簡単です．
$M = 6$ の値を知っているとすると，$\mathtt{110110}\mathtt{10}$ というビット列から「余り54,商2」を計算し，$2*2^M + 54 = 182$ といった具合に復号できます．

論文内では，適切な $M$ の値は容易に計算でき，かつ適切なパラメータを設定すれば符号化の冗長性（即ち，符号化によるエントロピーのロス）を 2 bits 以下にできると主張しています（本記事内では証明は行いません）．

Trits 符号化への応用

Spill-over encoding を用いて，長さ $N$ の trits $t$ を符号化しましょう．
まず，$t$ を $w$ trits 毎のブロックに分割します($w$ はワードサイズでしたね)．このときブロックの数は $\lceil N/w\rceil)$ 個です(図2参照)．
そして，各ブロックに spill-over encoding を適用すると，合計の冗長性は高々 $2 * \lceil N/w\rceil \in O(N/w)$ bits となります．

というわけで，冗長性が $O(N/w)$ bits, すなわち合計で $\lceil N\log_2{3} \rceil + O(N/w)$ bits の表現が得られました．
ただし，定数個のパラメータ (e.g., $M$) の値を別途覚えておく必要があるので，追加で $O(\log N)$ bits を利用します．
また，この表現があれば，元の $t$ の任意の要素に定数時間でアクセスすることができます(詳細は割愛します)．

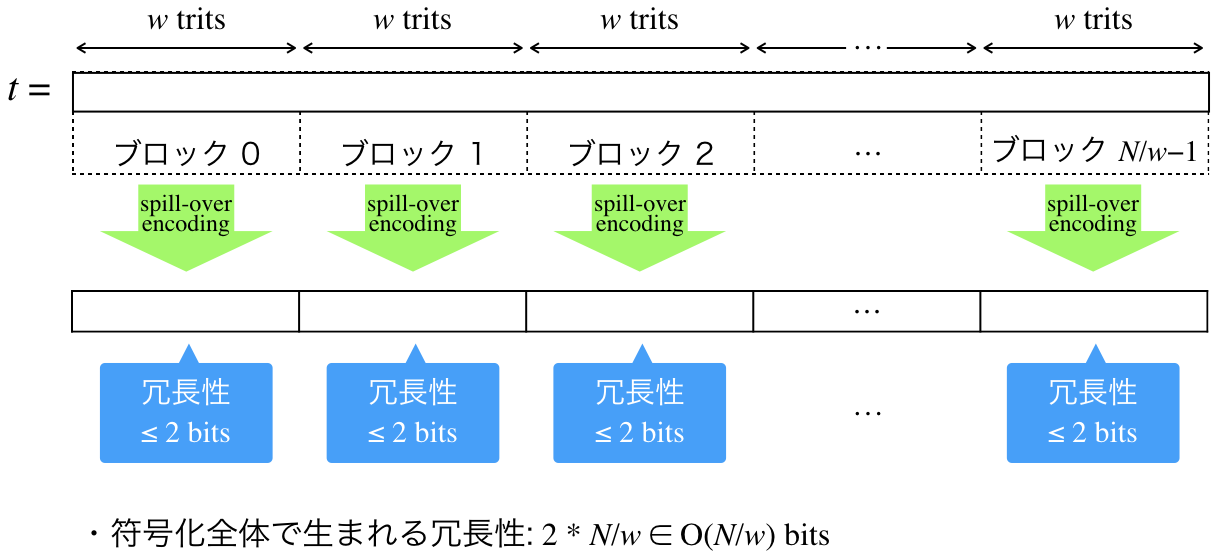
[図2. ブロック分割と spill-over encoding の概念図]

再帰による冗長性の削減

実は前述の $O(N/w)$ bits の冗長性は，$O(N/w^r)$ bits にまで減らすことができます($r$ は1以上の整数)．ただしこれはアクセス時間とのトレードオフになっていて，アクセス時間は $O(r)$ となります．

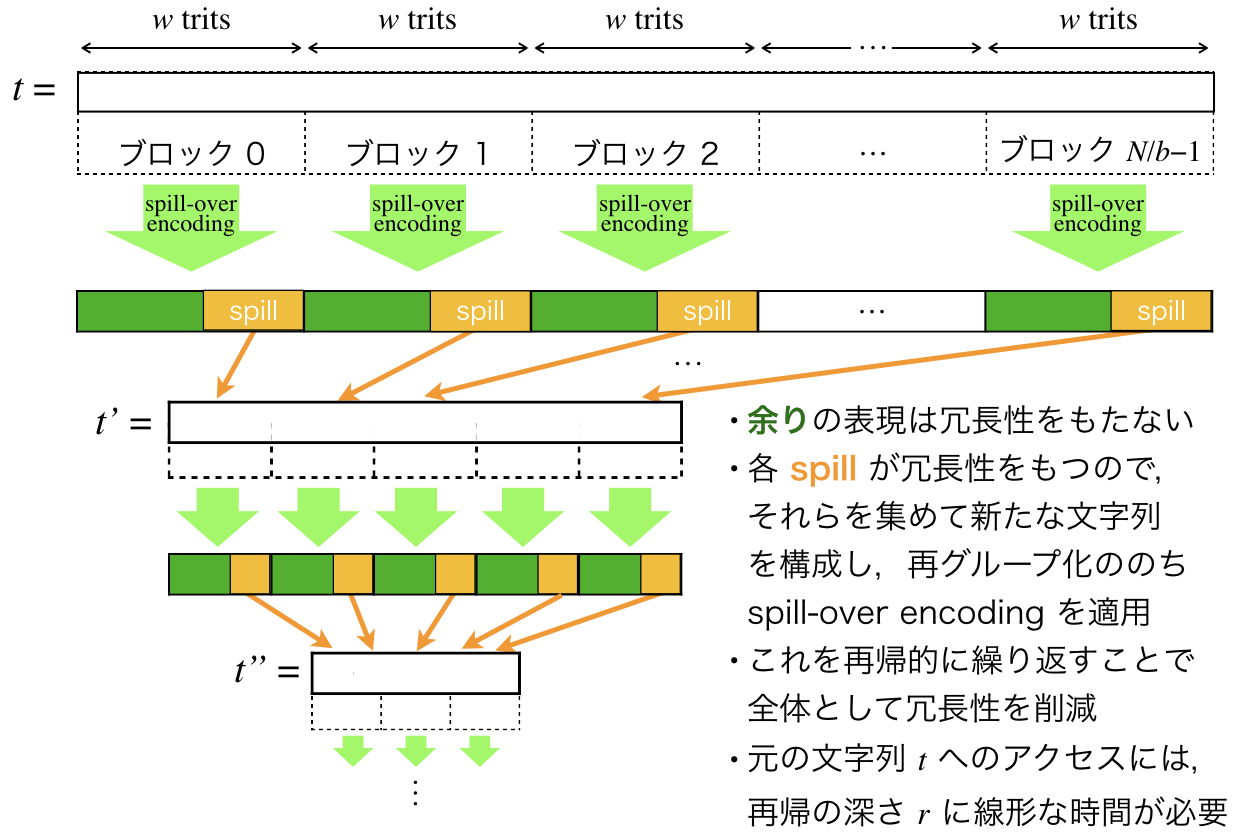
そのアイデアは，「spill を集めて再帰的に符号化する」です(図3参照)．
まぁよくぞこんなアイデアを思いつくなぁと感心します．そして，たったこれだけのアイデアで冗長性を削減できるのだからスゴい．
解析が気になる方は元論文をご参照ください．

[図3. spill を再帰的に符号化する概念図]

説明の簡単のために証明を省略したり解析を実際より緩く行ったりしましたが，アイデアと雰囲気を掴んでいただければ幸いです．

おわりに

いかがでしたか？
本記事では，trits (= 3進数 = 3種類の文字からなる文字列) を簡潔に表現する方法について紹介しました！
実用上は 5 trits を 8 bits に変換するだけでも十分に小さな表現が得られましたね！

省領域なデータ構造を考えているときに「あれ，この部分って trits じゃね？」って思ったら，
この記事で紹介した論文や実装を参考にしてみるといいことがあるかもしれませんね(^^)！

参考文献

Mihai Patrascu. Succincter. In Proc. 49th IEEE Symposium on Foundations of Computer Science (FOCS), pages 305–313, 2008.
@kampersanda. succinctrits. https://github.com/kampersanda/succinctrits

参考にした論文は著者のHPで公開されています． ↩
今回紹介するアルゴリズムでは実際のサイズは $8\cdot\lceil N/5\rceil$ bits となりますが，ここでは記述の簡単のため，$N$ は5の倍数だと暗黙に仮定しています． ↩
長さ $N$ の3進数の種類数は $3^N$ 種類であるので，それを表現するために必要なビット（情報理論的下界）は $N\log_2{3}$ bits であることがわかります．現実のビット数は整数値なので，$\lceil N\log_2{3}\rceil$ bits が最適なビット数であることが言えます． ↩
ちなみに，$b$ 番目のブロックに定数時間でアクセスできるのは，ブロックサイズが 8 bits で固定されているからです．もしも各ブロックのサイズがバラバラであったり，ブロックサイズがワードサイズに比べて極端に大きい場合は定数時間アクセスは難しいでしょう． ↩
succinct な trits なので "succinctrits" なんですね．素敵なネーミングです． ↩

3進数を簡潔に表現しよう