はじめに
https://qiita.com/ojiya/items/e98a9dd5cb6cd7ad38ca や https://qiita.com/ojiya/items/37b594150115531481f0 の記事に引き続き、PymatgenとOptunaを用いてXRDの解析を行う目的で、Pymatgenの機能を紹介している。この記事では、XRDスペクトルを計算する。と言っても、生真面目にやるわけではなく、結晶構造からピーク位置と強度を計算し、Voigt関数を足し合わせて粉末XRDパターンみたいなものを作るだけだ。先に断っておくと、ここで扱う情報だけでは、本当は粉末XRDパターンを計算することはできないのだが、「OptunaでXRDの解析をすることはできるのか」という仮説の検証ができるくらいにはシミュレーションができるので、一旦はこれで進めるか、と理解してもらいたい。それから、この文章はXRDの基本についてはわかっている人向けに書いている。そこの補足が欲しい場合は、要望があったら書きます。
実際のコード
PymatgenでのXRDピーク位置、強度の計算
まずは、例によって、Fe3O4の構造を読み込んで、変数matに格納する。
from pymatgen.io.cif import CifParser
path = 'Fe3O4_mp-19306_symmetrized.cif'
parser = CifParser(path)
mat = parser.get_structures(primitive=False, symmetrized=False)[0]
割と重要なポイントとして、通常は実験的に得られたXRDの指数を書く(例えばグラフに書き込む)ときはconventional cellを想定するので、ここでprimitive=Falseにしておかないと、計算されるピークの指数がめちゃくちゃになる(格子の取り方が違うので当たり前だが)。とあるサイトでは、これを見落としてピーク位置を計算したばかりに、ある有名な先生に口汚く罵られるということがあった。気をつけましょう。閑話休題。この構造をもとに、XRDパターンの計算を行う。まずは、ここでは、以下のようにモジュールXRDCalculatorを読み込んでくる。
from pymatgen.analysis.diffraction.xrd import XRDCalculator
次に、XRDパターンを計算するための条件を設定する。ここでいう条件とは、X線の波長とデバイ・ワラー因子(熱因子)を指す。X線はデフォルトではCuのKα1とKα2が設定されるようになっているので、実験室系では、多くの場合デフォルトで問題ないだろう。別の条件を使いたい場合は、文字列か小数で指定する。また、デバイ・ワラー因子は辞書型で与える。とりあえず、例を見てもらった方がわかりやすい気がする。
xrd_cond = XRDCalculator(wavelength='CuKa', debye_waller_factors={Element('Fe'):0.2, Element('O'):0.6})
# 文字列で指定する場合は、他に ('CuKa', 'CuKa2', 'CuKa1', 'CuKb1', 'MoKa', 'MoKa2', 'MoKa1', 'MoKb1',
# 'CrKa', 'CrKa2', 'CrKa1', 'CrKb1', 'FeKa', 'FeKa2', 'FeKa1', 'FeKb1', 'CoKa', 'CoKa2', 'CoKa1', 'CoKb1',
# 'AgKa', 'AgKa2', 'AgKa1', 'AgKb1')が使える。
# 小数で指定する場合は、例えば以下のようにする。
# xrd_cond = XRDCalculator(wavelength=1.54056, debye_waller_factors={Element('Fe'):0.2, Element('O'):0.6})
デバイ・ワラー因子は、見ての通り、keyがElement型で元素種、valueが因子になるように設定する。特に理由がなければ、室温では金属で0.2位、セラミックス中の非金属では0.6位が普通だろう。ここも最適化の対象にできるので、とりあえずはこれくらいの値にしておく。
続いて、反射位置と強度、指数を計算する。
xrd_calcd = xrd_cond.get_pattern(mat)
print(type(xrd_calcd)
# 出力:<class 'pymatgen.analysis.diffraction.core.DiffractionPattern'>
先ほど設定したシミュレーション条件に、.get_pattern(Structure型のデータ)という書き方で、計算させることができる。計算結果は、DiffractionPattern型のデータになっている。ここからデータを取り出すには、第一には、pymatgenのお約束、as_dictを使う方法。
dict_xrd_calcd = xrd_calcd.as_dict()
print(dict_xrd_calcd.keys())
# 出力:dict_keys(['@module', '@class', '@version', 'x', 'y', 'hkls', 'd_hkls'])
なんとなく想像がつくかもしれないが、'x'にピーク位置、'y'に強度、'hkls'に指数、'd_hkls'に面間隔が格納されている。もっとシンプルに取り出したい場合は、以下のようにできる。
calcd_x = xrd_calcd.x
calcd_y = xrd_calcd.y
calcd_hkls = xrd_calcd.hkls
calcd_d = xrd_calcd.d_hkls
いずれのデータもリスト型になっており、観測されるピークが、低角側から順番に格納されている。例えば、以下には一番低角側にあるピークの情報を取り出してみた。
print(calcd_x[0], calcd_y[0], calcd_hkls[0], calcd_d[0])
#出力:17.98985486665392 7.50841268512196 [{'hkl': (1, 1, 1), 'multiplicity': 8}] 4.926732808708708
これで、2θ = 17.99°に強度7.51、hkl = 111のピークがあり、その面間隔は4.93 Åである、ということがわかる。強度は相対値で、最強ピークが100になっていることに注意。これから、このピークの情報をもとに、粉末パターンをシミュレートする。
Voigt関数の定義と計算
粉末XRDのここのピークは、多くの場合、Voigt関数というGauss関数とLorentz関数の畳み込みの形で表すことができる。詳しくは、https://qiita.com/yamadasuzaku/items/4fccdc90fa13746af1e1 をご覧ください。また、この関数をpythonで計算する方法も、ここからいただくことにする。
import matplotlib.pyplot as plt
import numpy as np
import scipy as sp
import scipy.special
def voigt(xval,params):
norm,center,lw,gw = params
z = (xval - center + 1j*lw)/(gw * np.sqrt(2.0))
w = scipy.special.wofz(z)
model_y = norm * (w.real)/(gw * np.sqrt(2.0*np.pi))
return model_y
XRDを計算するときは、normが強度、centerがピーク位置になる。例えば、ピーク一本だけなら、次のように計算させることができる。
x = np.arange(10,60,0.02)
params = [calcd_y[0], calcd_x[0], 0.02, 0.02]
one_peak = voigt(x, params)
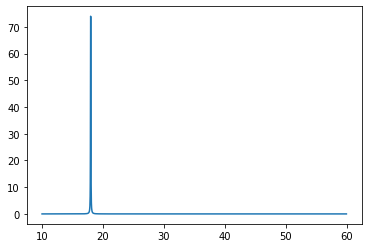
plt.plot(x, one_peak)
これで、以下の図が出力される。
粉末XRDパターンの計算
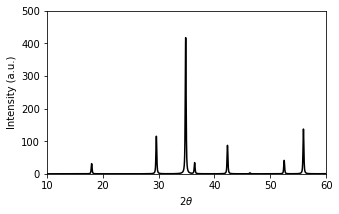
あとは、全てのピークを足し合わせれば、粉末パターンを得ることができる。ここでは、要素が全て0であるような配列、calcd_patternを作っておいて、それに順々に足していくコードになっている。ついでに、真面目にグラフも書いておいた。
calcd_pattern = np.zeros(len(x))
N = len(calcd_x)
for i in range(N):
norm = calcd_y[i]
center = calcd_x[i]
lw = 0.05
gw = 0.05
params = [norm, center, lw, gw]
calcd_pattern += voigt(x, params)
figure = plt.figure(figsize=(5,3))
ax = figure.add_subplot(111)
ax.plot(x, calcd_pattern,color='0')
ax.set_xlim(10, 60)
ax.set_ylim(0, 500)
ax.set_xlabel(r'2$\theta$')
ax.set_ylabel('Intensity (a.u.)')
今回の記事は以上。