深層学習で数理最適化問題を解く【前編】

この記事は BrainPad Advent Calender 2019 初日の記事です。が、いきなり日をまたいで1日オーバしてしまいました。申し訳ありません 🙇

深層学習がいろいろな分野で応用されていますが、数理最適化問題に適用しようという動きがあります。この記事では、そのなかでも特に、いろいろな状況下で最適な道順を見つける「ルーティング問題」にとりくんだAttention, Learn to Solve Routing Problems!という論文について紹介し、TensorFlow2.0で実装していこうと思いますが、今回は前編として問題の背景とネットワークの構築まで。学習アルゴリズムと学習結果はまだちゃんと訓練できていないので後編で紹介します。

数理最適化と機械学習

ときどき「数理最適化」と「機械学習」の違いは何ですか？と聞かれることがあります。
まず、広い意味で「数理最適化」とは、「数理的なアプローチで最適化すること」で、「最適化」とは何らかの関数を最小化（もしくは最大化）することです。

例えば「渋谷駅までの最適な道を知りたい」という言葉の裏には、「最も短い時間で渋谷駅につきたい」とか、「最も少ない金額で渋谷駅につきたい」という意味合いが、「広告の出稿を最適化したい」と言ったときには「予算を守りつつ、クリック数を最大化したい」とか「制約を満たしつつ、予算とのギャップを最小にしたい（予算を使い切りたい）」という意味合いが含まれています。

一方で「機械学習」は、ざっくりといって「データからパターンを見つけ出すこと」です。多くの機械学習手法では訓練の過程で損失関数を最小化しているので、数理最適化の利用例の一つということもできるかと思います。また、例えば分類問題であれば、間違分類の数を最小化しようと数理的にアプローチしているので、機械学習自体が数理最適化の手法の一つと捉えることもできるかもしれません。

ただし、機械学習の目的は（たとえ訓練が関数の最小化であっても、やりたいことは）必ずしも関数の最小化ではないので、機械学習は数理最適化の一つと言い切ることもできないと思います。「データからパターンを見つけ出すこと」と「数理的なアプローチで最適化すること」は、互いに関係していますが、そもそも視点の違うものなので、比較すること自体がナンセンスなように感じます。

ただ、仕事でお客さんと話しているときにでてくる「数理最適化」という言葉はもう少し狭義の意味を持っていることが多く、個人的には

1. 機械学習の目的は予測すること
2. 数理最適化の目的は（予測結果をもとに）最適なアクションを見つけること

という感じに割り切って説明をしています。

今回紹介する論文「Attention, Learn to Solve Routing Problems!」で取り上げているルーティング問題は、利用できる車両の台数や、運べる荷物の量、遵守すべき交通ルール、従業員間の仕事量の均一化など、様々な制約があるなかで、最適なルートを見つけ出すような問題です。上記の分け方ではまさに 2.数理最適化 に当たりますが、それに機械学習（深層強化学習）を使って取り組む、というところに面白さを感じました。

同種の問題に取り組んでいる論文Neural Combinatorial Optimization with Reinforcement Learningの紹介記事（巡回セールスマン問題を深層強化学習で解いてみる @ panchovie さん）もご覧ください。

深層強化学習によるアプローチの良い点と悪い点

数理最適化の手法としては、数理計画法を用いた方法や（メタ）ヒューリスティクスを用いた方法などいくつかありますが、今回の論文で使用している深層強化学習によるものの面白い点は以下のとおりです。

• 目的関数（最小化したい関数）を自由に設計できる
  • 数理計画法によるものの場合、目的関数を数式に落とし込まなければならず、数式の形にもかなりきつい制限がある（数値が与えられれば良いわけではなく、数式として表現されている必要がある）が、深層強化学習によるものの場合は、数値され与えられれば最適化できる（ブラックボックス最適化）
• 速度が（問題の規模について）安定していて、ある程度高速
  • 訓練には時間がかかるが、一度訓練してしまえば、様々な問題を高速に解くことができる
• 挙動の意味が理解しやすい
  • 深層強化学習の場合、各状況での判断自体を数値で表現するため挙動が理解しやすい（例えば「とりあえず近場を選ぶ」などのルールがある程度見て取れる）

逆に課題だなと感じる点は

• 複雑な制約をどのように組み込んだらよいかわからない
  • 数理計画法による場合、かなりの自由度をもって制約をいれることができるが、深層強化学習による手法では、ネットワーク構造や訓練方法にうまく制約を組み込む必要があり、（少なくとも知見の蓄積・共有されていない現在では）職人技が必要になります。
• シミュレーターが必要
  • 前述の通り、（深層強化学習を含む）機械学習は「データからパターンを見つける」ものなので、訓練にはデータが必要です。また、多数の繰り返しが必要なため、シミュレーターが必要になります。問題が簡単な場合は良いのですが、問題が複雑になってくると、シミュレーターの実装が大変になる可能性があります。
• 最適性の保証がない
  • 数理計画法のソルバーの場合、厳密に最適化どうか、あとどれくらい改善の余地がありそうか、といった情報を得ることができ、アルゴリズムの開発や実運用時の参考情報として利用できます。深層強化学習による方法の場合、厳密にそれを知る術はありません。（推定することはできると思います）

数理最適化したい！と思った際には、上記のような点に気をつけて手法を検討する必要があります。

TensorFlow 2.0

9/30にリリースされたTensorFlow 2.0 では、いわゆる Define By Run の Eager Execution がデフォルトのモードとなりました。Define By Run はPFNが開発しているChainerによって提案された計算グラフの構築方法で、動的に変化するような計算グラフに適しています。ルーティング問題は、様々な条件や拠点の数などで計算グラフの構造が変化するので、TensorFlow 2.0 の検証の意味も含め、ゼロから実装してみました（正確にはまだいじっている最中なので、下記のコードは随時更新していく予定です）。
なお、上記の論文について、作者がPyTorchによる実装を公開しているので、利用したいだけの場合はそちらを利用するのが良いでしょう。

論文の3行要約

1. VRP、OP、TSPなど、様々なルーティング問題を解く深層強化学習モデルを提案
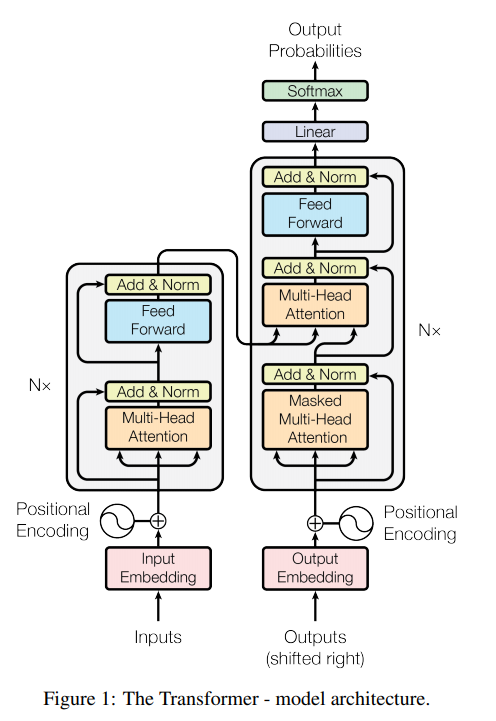
2. 本手法ではTransformerをベースにしたモデルを利用
3. 個別の問題に特化してチューニングされた既存のアルゴリズムに近い結果が得られることを確認

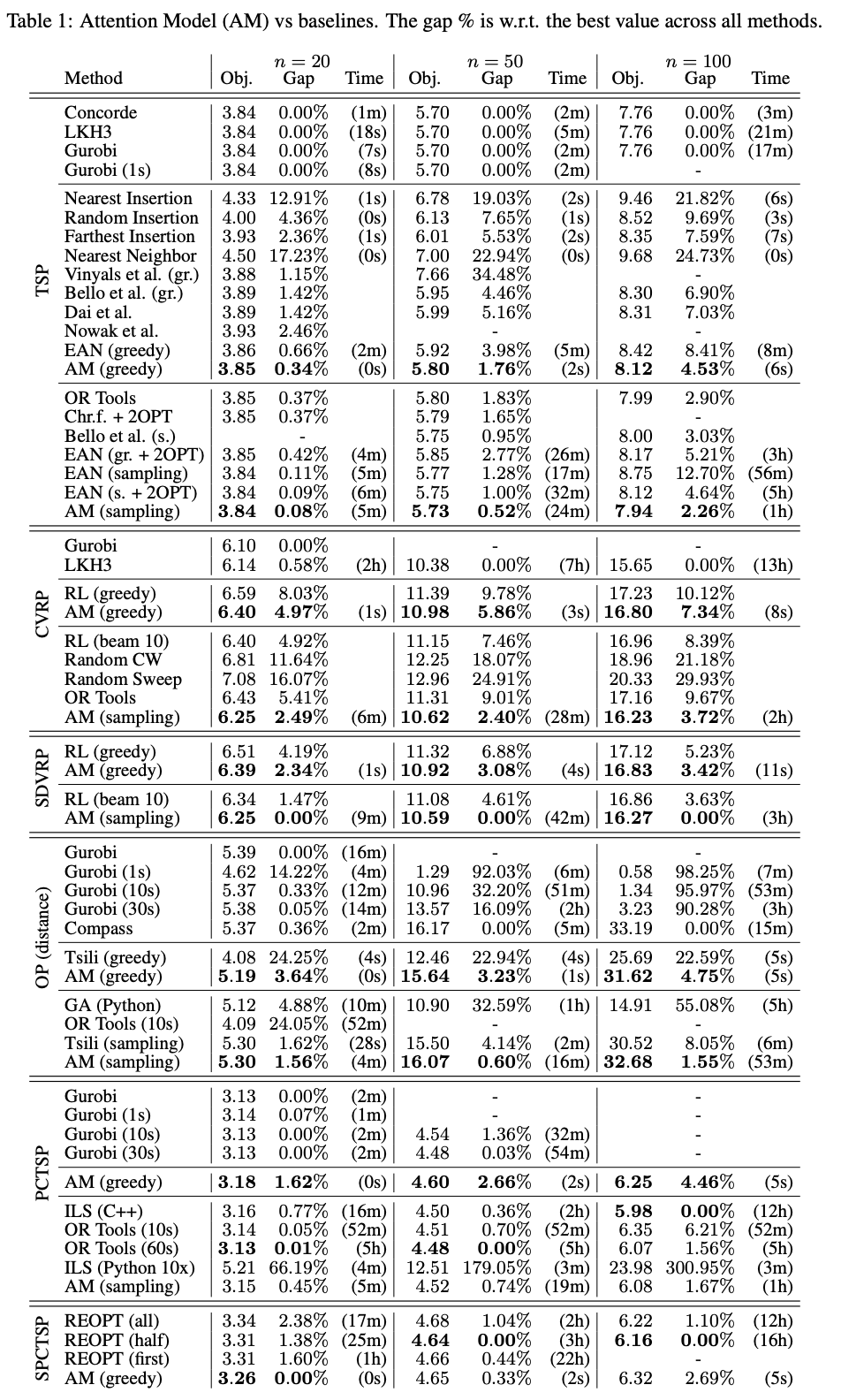
いろいろなサイズのいろいろなルーティング問題に対して実験した結果は以下のとおりです（論文より抜粋）。AM(greedy) と AM(sampling) が提案手法です。Gurobiのように厳密解を求めるわけではないので、最適解とのギャップがありますが、$n=100$という規模の大きめの問題についても、そこそこの時間でそこそこの性能を示していることがわかります。比較対象の多くが、それぞれの問題のために最適化されたアルゴリズムを利用していることを考えると、すごい結果のように思います。

アルゴリズムの概要

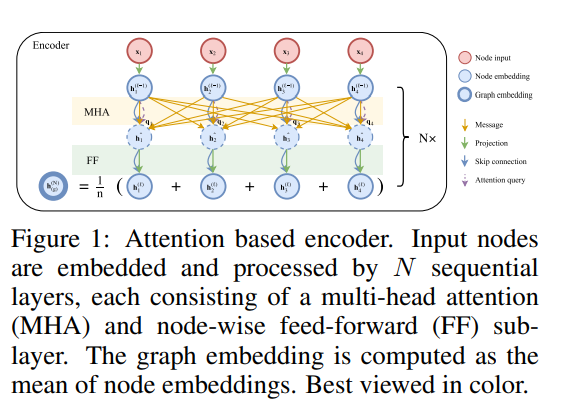
利用するネットワークは、いわゆる Encoder-Decoder 型のものです。

1. Encoder: Transformerというモデルをベースにしたネットワークです。
   • 入力: 各拠点の座標と拠点毎の需要などの情報
   • 出力: 各拠点の埋め込み表現
2. Decoder: Decoderでは、Attention を使って、既に訪れた拠点をマスクしながら一拠点ずつ推定していきます。
   • 入力: Encoderの出力（各拠点の埋め込み表現）
   • 出力: 訪れる拠点のリスト（訪問時間順）

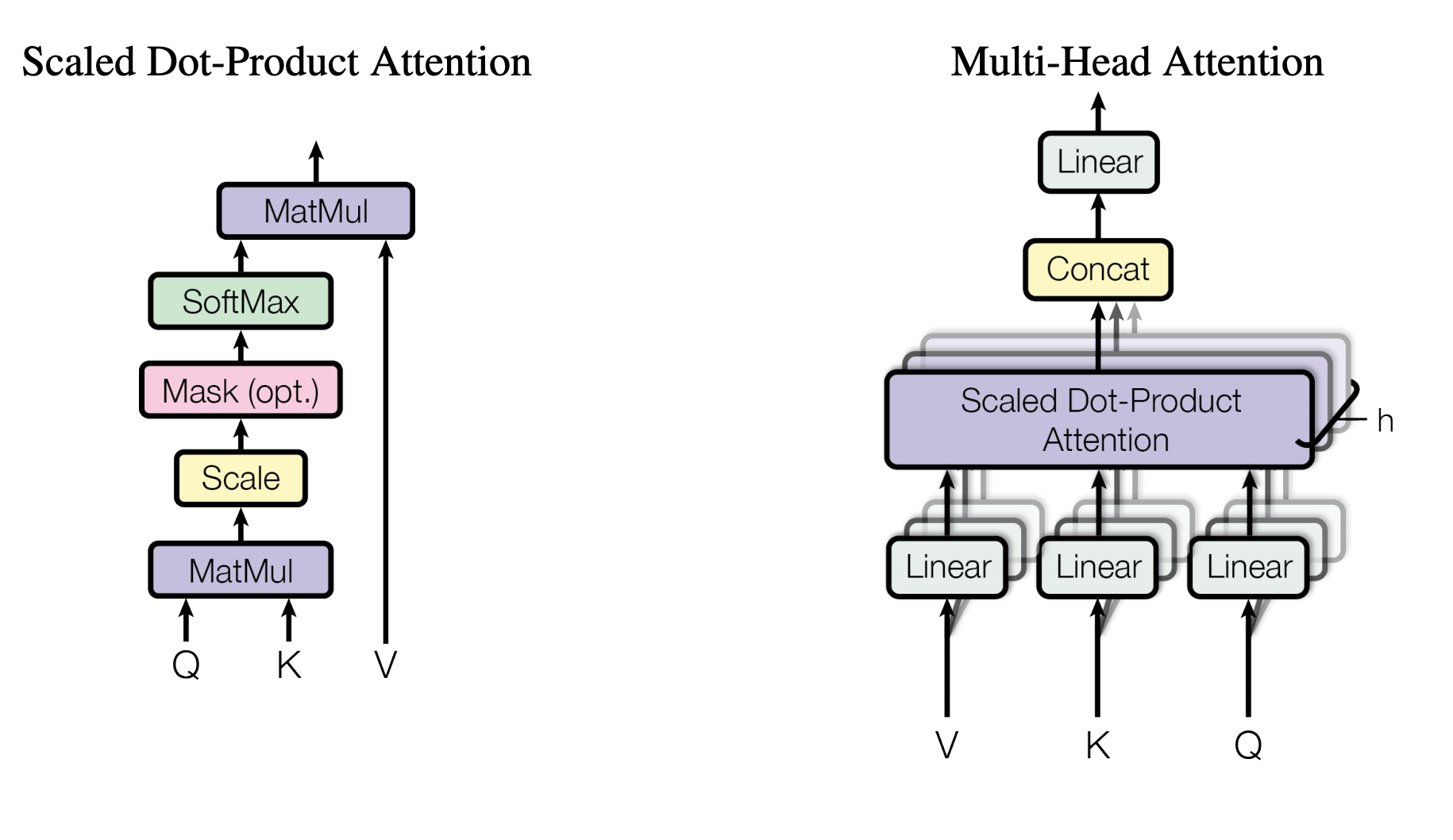
Transformerは自然言語処理で最近流行っている様々なモデルのベースとなっているもので、こちもAttentionと呼ばれる機構を利用しています。EncoderもDecoderもAttentionがベースとなっていいるため、論文のタイトルも「Attention」から始まります。なお、訓練には以下のようなREINFORCEアルゴリズムを用います。

具体的な訓練ステップは後編にゆずり、ここではネットワークを TensorFlow 2.0 で実装していくステップを見ていきます。

Encoder

前述の通り、基本的な構造は Transformer と同じものです。Transformerについての解説と実装方法についてはこちらのQiita記事 がとても参考になります。2.0ではないですが、TensorFlowで書かれているため、特にEncoderについては、とても似たコードになります。

AttentionLayer

TensorFlow2.0 では、 Keras が標準の高レベルAPIとなりました。そのため、処理の単位をレイヤーとして定義していきます。 それには、 以下のように、keras.layers.Layer を継承して、 call メソッドを再定義すればOKです。

class CustomLayer(keras.layers.Layer): # keras.layers.Layerを継承
    def __init__(self, ..., **kwargs):
        super().__init__(**kwargs)
        # 変数の定義などの初期化処理
        ...

    def call(self, inputs, mask=None):
        # inputs には入力テンソル（もしくは入力テンソルのリストがはいる）
        # マスキング処理をする場合は mask 引数を指定する
        ...

今回の場合、推論結果に上下限を設定するための clip引数や、往訪済のノードを無視するための mask 引数があるため、若干複雑ですが、Attentionレイヤーは、以下のように記述できます。

class DotProductAttentionLayer(keras.layers.Layer):
    def __init__(self, clip=None, return_logits=False, inf=1e+10, **kwargs):
        super().__init__(**kwargs)
        self.clip = clip
        self.return_logits = return_logits
        self.inf = inf

    def call(self, inputs, mask=None):
        """
        Arguments:
            inputs (List[tf.Tensor]): [query, key, value] with
                query (tf.Tensor): Tensor with shape (batch_size, n_queries, n_qunits),
                key (tf.Tensor): Tensor with shape (batch_size, n_keys, n_kunits)
                value (tf.Tensor): Tensor with shape (batch_size, n_values, n_vunits)
            mask (tf.Tensor): Tensor with shape (batch_size, n_keys, 1), defaults to None.

        Returns:
            (tf.Tensor): Tensor with shape (batch_size, n_queries, n_vunits) if return_logits=False, (batch_size, n_queries, n_keys) if return_logits=True
        """
        query, key, value = inputs
        logit = tf.matmul(key, query, transpose_b=True)/np.sqrt(value.shape[2])
        if self.clip is not None:
            logit = self.clip*tf.tanh(logit)
        if mask is not None:
            with tf.name_scope('mask'):
                logit = logit - self.inf*tf.cast(mask, logit.dtype)

        if self.return_logits:
            return tf.transpose(logit, perm=(0, 2, 1))

        prob = tf.nn.softmax(logit, axis=1)
        return tf.matmul(prob, value, transpose_a=True)

Transformerでは、上記のAttentionを複数並列で適用させて、前後にLinearレイヤを挟むことで、性能の向上をはかっています。これをMHA(Multi Heads Attention)と呼びます。

class MultiHeadsAttentionLayer(keras.layers.Layer):
    def __init__(self, units, n_heads, dim_key=None, attention_class=DotProductAttentionLayer, **kwargs):
        super().__init__(**kwargs)
        self.units = units
        self.n_heads = n_heads
        self.dim_value = self.units // self.n_heads
        self.dim_key = dim_key if dim_key else self.dim_value
        self.attention_class = attention_class

        self.concat = keras.layers.Concatenate()
        self.output_layer = keras.layers.Dense(units)
        self.attentions = [
            self.attention_class()
            for _ in range(n_heads)
        ]
        self.query_layers = [
            keras.layers.Dense(self.dim_key)
            for _ in range(n_heads)
        ]
        self.key_layers = [
            keras.layers.Dense(self.dim_key)
            for _ in range(n_heads)
        ]
        self.value_layers = [
            keras.layers.Dense(self.dim_value)
            for _ in range(n_heads)
        ]

    def call(self, inputs, mask=None):
        """
        Arguments:
            inputs (List[tf.Tensor]): [query, key, value] with
                query (tf.Tensor): Tensor with shape (batch_size, n_queries, n_qunits),
                key (tf.Tensor): Tensor with shape (batch_size, n_keys, n_kunits)
                value (tf.Tensor): Tensor with shape (batch_size, n_values, n_vunits)
            mask (tf.Tensor): Tensor with shape (batch_size, n_keys, 1), defaults to None.

        Returns:
            (tf.Tensor): Tensor with shape (batch_size, n_queries, n_vunits)
        """
        outputs = [
            attention([query_layer(query), key_layer(key), value_layer(value)], mask=mask)
            for attention, query_layer, key_layer, value_layer
            in zip(self.attentions, self.query_layers, self.key_layers, self.value_layers)
        ]
        return self.output_layer(self.concat(outputs))

TensorFlow2.0では、 __init__メソッドの中でレイヤを組み合わせて利用することができます。TensorFlow1.xの時のように、buildメソッドの中で定義して訓練対象の変数を明示的に追加する必要はありません。

maskを考慮に入れなければ、Attention機構の入力は (query, key, value) ですが本論文では queryもvalueもkey自身という SelfAttention を使っています。

class SelfAttentionLayer(keras.layers.Layer):
    def __init__(self, impl, **kwargs):
        super(SelfAttentionLayer, self).__init__(**kwargs)
        self.impl = impl

    def call(self, x, mask=None):
        return self.impl([x, x, x], mask=mask)

上記のように、別のレイヤのラッパーを定義することもできます。

TransformerBlock

レイヤの出力に、レイヤの入力を足し合わせる残差ブロック（ResidualBlock）と呼ばれる構造があります。画像認識などでは、通常のレイヤの代わりに残差ブロックを使うことで性能が上がることが知られています。今回の論文でも ResidualBlock を利用するので、以下のように定義しておきます。

class ResidualBlock(keras.layers.Layer):
    def __init__(self, inner_layer, normalization_layer, **kwargs):
        super(ResidualBlock, self).__init__(**kwargs)
        self.inner_layer = inner_layer
        self.normalization_layer = normalization_layer
        
    def call(self, inputs, mask=None):
        if mask is None:
            return self.normalization_layer(inputs + self.inner_layer(inputs))
        else:
            return self.normalization_layer(inputs + self.inner_layer(inputs, mask))

normalization_layer には BatchNormalization を使うことが多いのですが、今回の論文では、BatchNormalization以外の方法も検証しているようなので、引数にしています。
Encoder は、MHAに全結合層を加えたものを$N$回繰り返し、その結果を出力としています。上述の ResidualBlock と組み合わせると、1回分は以下のようにかけます。

class TransformerBlock(keras.layers.Layer):
    def __init__(self, n_heads, dim_hidden, attention_class=DotProductAttentionLayer, activation='relu', **kwargs):
        super().__init__(**kwargs)
        self.n_heads = n_heads
        self.dim_hidden = dim_hidden
        self.attention_class = attention_class
        self.activation = activation

    def build(self, input_shape):
        self.attention_layer = ResidualBlock(
            SelfAttentionLayer(MultiHeadsAttentionLayer(
                units=input_shape[2],
                n_heads=self.n_heads,
                attention_class=self.attention_class
            )),
            keras.layers.BatchNormalization()
        )
        self.dense_layer = ResidualBlock(
            keras.models.Sequential((
                keras.layers.Dense(self.dim_hidden, activation=self.activation),
                keras.layers.Dense(input_shape[2], activation=self.activation)
            )),
            keras.layers.BatchNormalization()
        )
        super().build(input_shape)

    def call(self, inputs, mask=None):
        return self.dense_layer(self.attention_layer(inputs, mask=mask))

今までと違い、 build メソッドの中でレイヤーを定義しています。buildメソッドには引数としてinput_shapeが渡されるため、入力テンソルの形によって初期化の方法が違うため__init__では定義できないような変数やレイヤは、こちらで定義します。super().build(input_shape)は忘れないようにしましょう。

Encoder

上記をまとめて Encoder を構築します。最初に全結合層を入れて次元をかえたあとでTransformerBlockを単純に積み上げているだけです。

class Encoder(keras.Model):
    def __init__(self, emb_dim=128, n_layers=3, n_heads=8, dim_hidden=128, attention_class=DotProductAttentionLayer, activation='relu', **kwargs):
        super().__init__(**kwargs)
        self.emb_dim = emb_dim
        self.emb = keras.layers.Dense(emb_dim)
        self.transformers = [
            TransformerBlock(
                n_heads=n_heads,
                dim_hidden=dim_hidden,
                attention_class=attention_class,
                activation=activation
            )
            for _ in tf.range(n_layers)
        ]

    @tf.function
    def call(self, inputs):
        """
        Arguments:
            inputs (tf.Tensor): tf.Tensor with size (batch_size, n_nodes, dim)

        Returns:
            (tf.Tensor): (batch_size, n_nodes, self.emb_dim)
        """
        x = self.emb(inputs)
        for transformer in self.transformers:
            x = transformer(x)
        return x

今までと違うのは2点。keras.layers.Layer ではなく keras.Model を継承している点と、callメソッドに @tf.function がついている点です。

まず、keras.Model は、 keras.layers.Layer を継承しているため、レイヤーがわりに使えます。また、fitなど、レイヤには存在しなかったメソッドが追加されます。ある程度の規模となったところで keras.Modelとしておき、適当な問題で訓練させてみることで、実装に間違いがないか検証できます。

次に、@tf.function です。このデコレーターを付けられたメソッドは、内部の処理をTensorFlowのグラフに変換されます。それにより、関数の実行が最適化され、高速になります。これまでのメソッドにつけても良いのですが、@tf.functionをつけると、形状の違うテンソルが入力されるごとにTensorFlowのグラフの構築処理が走るなど、ちょっと癖のある挙動となります。また、小さくつけることに速度的な意義はあまりないので、大きめの単位で使うのがおすすめです。

Decoder

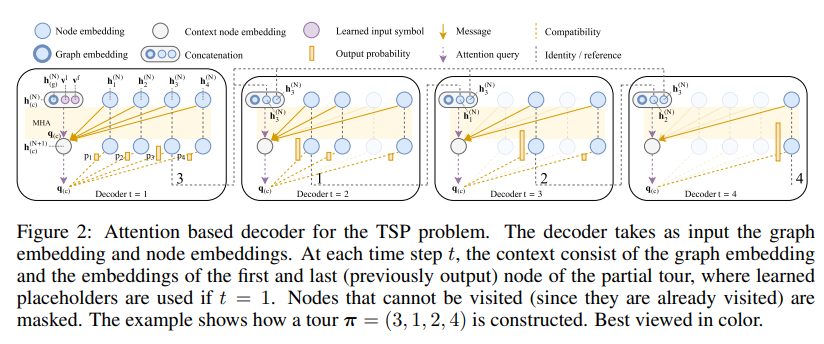
さて、次は Decoder です。下図のように、Decoderでは、Attentionを2つ使います。
1つめのレイヤーで query を決定し、2つめのレイヤーで 次に進むべきノードを決定します。

より具体的には、まず context と呼ばれるベクトル

$$h_{(c)} = [\bar{h}, h_{\pi_{t-1}}, h_{\pi_{1}}]$$

を定義します。ここで、 $h_{\pi_i}$ は、$i$番目のノードの埋め込み表現で、Encoderの$i$番目の出力、$\bar h$ はすべての埋め込みの平均を表します（$\bar h = \frac{1}{2}\sum_{i}h_{i}$）。 このベクトルは、 $\bar h$ がグラフ全体の情報を、$h_{\pi_{t-1}}$ が直前に訪れた拠点の情報、$h_{\pi_{1}}$ が、スタート拠点（〜最後に戻っていく拠点）を表していて、なんとなく人間がルートを考えるときに必要な情報が含まれています。また、拠点を訪れるたびに $h_{\pi_{1}}$ がかわるので、contextと呼ばれています。

Decoder の最初の Attention では、

• query: context $h_{(c)}$
• key: ノードの埋め込み表現 $h_{\pi_{t}}$
• value: ノードの埋め込み表現 $h_{\pi_{t}}$ (key と同じ)

とし、その出力を 2層目の Attention の query とします。2層目は

• query: 1層目の Attention の出力
• key: ノードの埋め込み表現 $h_{\pi_{t}}$
• value: ノードの埋め込み表現 $h_{\pi_{t}}$ (key と同じ)

の Attention ですが、value を使うわけではないので、単に query と key の内積をとって、最も近い拠点を選択するような働きをします。

この2つのアテンションを、訪問済の拠点をマスキング（つまり、Attentionの候補にしないようにしていく）しながら、繰り返し適用していくのが Decoder の流れです。

Decoder の1ステップ分の処理は以下のとおりです。

class DecoderCell(keras.layers.Layer):
    def __init__(self, n_heads, clip=10., attention_class=DotProductAttentionLayer, **kwargs):
        super().__init__(**kwargs)
        self.n_heads = n_heads
        self.clip = clip
        self.attention_class = attention_class

    def build(self, input_shape):
        context_shape, node_shape = input_shape
        self.prep_attention_layer = MultiHeadsAttentionLayer(
            units=node_shape[2],
            n_heads=self.n_heads,
            attention_class=self.attention_class
        )
        self.final_attention_layer = self.attention_class(return_logits=True, clip=self.clip)
        super().build(input_shape)

    def call(self, inputs, mask=None):
        """
        Arguments:
            inputs (List[tf.Tensor]): List of tf.Tensor represents context (batch_size, 1, 3*dim_emb) and tf.Tensor of nodes (batch_size, num_nodes, dim_emb)

        Returns:
            tf.Tensor with shape (batch_size, 1, num_nodes)
        """
        context, nodes = inputs
        query = self.prep_attention_layer([context, nodes, nodes], mask=mask)
        logit = self.final_attention_layer([query, nodes, nodes], mask=mask)
        return logit

DecoderCell から出力された logit はあくまで連続地値（より正確には確率のもととなる正規化されていない数値）なので、次の拠点を1つ決めるには、 Sampling を行う必要があります。Samplingの仕方には、logitを確率とみなす方法や、単純に値の高いものを順に撮ってくる方法など、複数あるので、これもレイヤーとして定義しておきます。

class Sampler(keras.layers.Layer):
    def __init__(self, n_samples=1, **kwargs):
        super(Sampler, self).__init__(**kwargs)
        self.n_samples = n_samples


class TopKSampler(Sampler):
    def call(self, logits):
        return tf.math.top_k(logits, self.n_samples).indices


class CategoricalSampler(Sampler):
    def call(self, logits):
        return tf.random.categorical(logits, self.n_samples, dtype=tf.int32)

DecoderCellを定義できたら、これとSamplerを組み合わせて、拠点を回り尽くすまでループで回せば Decoder の完成です。
TensorFlow2.0 では、普通にループを書くこともできますが、@tf.functionを使う場合は TensorArray と tf.range を組み合わせて使うと、自動的に最適化してくれます。

class Decoder(keras.Model):
    def __init__(self, cell, max_len=None, return_labels=False, sampler="categorical", **kwargs):
        super().__init__(**kwargs)
        self.max_len = max_len
        self.cell = cell
        self.sampler = get_sampler(sampler)
        self.return_labels = return_labels

    def build(self, input_shape):
        dummy_shape = (1, input_shape[2])
        # t=1のときのみ、コンテキストにはダミー変数を使う （t=1だと直前に訪れた拠点というものが存在しないので）
        self.dummy_first = self.add_weight(
            'dummy_first',
            shape=dummy_shape
        )
        self.dummy_last = self.add_weight(
            'dummy_last',
            shape=dummy_shape
        )
        super().build(input_shape)

    @tf.function
    def call(self, x):
        print("Trace: Decoder.call")
        input_shape = tf.shape(x)
        batch_size = input_shape[0]
        seq_len = input_shape[1]
        dim = input_shape[2]
        mask = tf.zeros_like(x[:, :, :1])

        graph_emb = tf.reduce_mean(x, axis=1, keepdims=True)
        dummy_first = tf.map_fn(lambda x: self.dummy_first, x[:, 0, 0])
        dummy_last = tf.map_fn(lambda x: self.dummy_last, x[:, 0, 0])
        context = tf.concat((graph_emb, dummy_first, dummy_last), axis=2)

        route = tf.TensorArray(dtype=x.dtype, size=self.max_len, clear_after_read=False, infer_shape=False)
        labels = tf.TensorArray(dtype=tf.int32, size=self.max_len, infer_shape=False)
        logits = tf.TensorArray(dtype=self.cell.dtype, size=self.max_len, infer_shape=False)
        for i in tf.range(self.max_len):
            logit = self.cell([context, x], mask)
            logits = logits.write(i, logit)
            label = self.sampler(tf.squeeze(logit, axis=1))
            labels = labels.write(i, label)
            one_hot = tf.one_hot(label, depth=seq_len)
            mask = mask + tf.transpose(one_hot, (0, 2, 1))
            route = route.write(i, tf.matmul(one_hot, x))
            context = tf.reshape(tf.concat((graph_emb, route.read(0), route.read(i)), axis=-1), tf.shape(context))

        logit = tf.transpose(logits.stack(), perm=(2, 1, 0, 3))[0]
        if self.return_labels:
            labels = tf.transpose(labels.stack(), perm=(2, 1, 0))[0]
            return logit, labels
        else:
            return logit

これで、EncoderとDecoderを実装できました。次回はこれをもとに、訓練を回し、実際に問題を解いてみたいと思います。（できるとは言っていない）

実装でハマりそうな点

今回のネットワークを構築する上で、いくつかハマりそうだなとおもった点があったので、備忘録を兼ねてまとめておこうと思います。

1. tf.function の使いどころ

   • 文中でも触れましたが、tf.functionはちょっと挙動が特殊なので、乱用しないほうが良さそうです。なので、基本的にはレイヤーではなくモデルくらいの大きな単位で指定してみて、うまく動かなかったら直す、というが書きやすいように思います。こういうのは細かく指定したくなるのですが、再利用時に無意味にハマることを回避するためにも、細かく指定しないほうが良さそうです。（公式ドキュメントにも、細かく指定しないほうがよいと書かれています）

2. tf.function でくくった場合は、 tf.range と TensorArray をつかう

   • はじめは普通の for loop で回していたのですが、あまりに遅かったので、 tf.range と TensorArray を使うと劇的に速くなりました。ただ、きちんと調査できていないのですが、どうも tf.function を指定している場合と指定していない場合で挙動が変わるようなので、ちょっと悩ましいです。

3. input_signatures と saved model

   • TensorFlow2.0 では、 keras.Model を save メソッドで一発で saved_model に変換できます。 saved_model になると、TensorFlow Serving や TensorFlow Lite など、TensorFlowエコシステムに乗っかることができるので便利なのですが、callメソッドに@tf.functionを付けた場合、input_signatures をどう指定するかで、保存のされ方が異なります。悩ましいなと思ったのは、@tf.functionアノテーションの引数には、（当然ですが）インスタンス変数を指定できないこと。input_signaturesは、入力テンソルの形状などを指定するのに利用します。例えば DenseLayer だと入力テンソルの形状を (None, 3) みたいにしていしますが、これは、1次元目（バッチ方向）は何でもOKで2次元目の大きさは 3 でありなさい、という意味になります。問題は2次元目を3固定ではなく、インスタンスごとに変えたい場合です。Kerasの思想としてはbuildが走った時点で2次元目の大きさが固定されるはずですが、アノテーションの引数ではそれを指定できない。また、(None, None)のように指定できるかといえば、buildした時点で2次元目が固定されるので、それもできない。ちょっと悩ましい。

4. BatchNormalization と SavedModel

   • これも、ちょっとちゃんと調査できていないのでもしかしたらバグかもしれないのですが、BatchNormalizationが K.learning_phase を使っているので、カスタムレイヤで BatchNormalization を使って、それを saved_model に保存して、再度読み込もうとすると、 learning_phase はどうなったんや、というエラーが出ます。K.set_learning_phase を呼べば解決できますが、それが正しい対処法なのかよくわかっていません。

5. 型ヒント

   • Python3.5以降では def hoge(hage: int): みたいに変数の型を指定することができます。この指定をしていると、saved_model への変換が失敗するようです。セコセコ tf.Tensor ってかいていたんですが、 saved_model つくってみよう、って思ったときに気がついて、一生懸命はずしました。

まとめ

深層学習で数理最適化問題を解く【前編】と題して、いろいろな状況下で最適な道順を見つける「ルーティング問題」にとりくんだAttention, Learn to Solve Routing Problems!という論文について紹介し、ネットワークを構築しました。後編では、といくつかの問題に適用してみた結果を掲載しようと思います。あと、それに合わせてコードも更新しようと思います。