対象とする方
- 単回帰分析・重回帰分析がいまいち分からなくて理解したい方
はじめに
重回帰分析をwikipediaで調べてみると以下のとおりでした。
Wikipediaより
重回帰分析(じゅうかいきぶんせき)は、多変量解析の一つ。回帰分析において独立変数が2つ以上(2次元以上)のもの。独立変数が1つのものを単回帰分析という。
一般的によく使われている最小二乗法、一般化線形モデルの重回帰は、数学的には線形分析の一種であり、分散分析などと数学的に類似している。適切な変数を複数選択することで、計算しやすく誤差の少ない予測式を作ることができる。重回帰モデルの各説明変数の係数を偏回帰係数という。目的変数への影響度は偏回帰係数は示さないが標準化偏回帰係数は目的係数への影響度を示す。
よくわかりませんよねー
わかりやすくするためにまず単回帰分析について例を交えて説明をします。
単回帰分析とは・・・
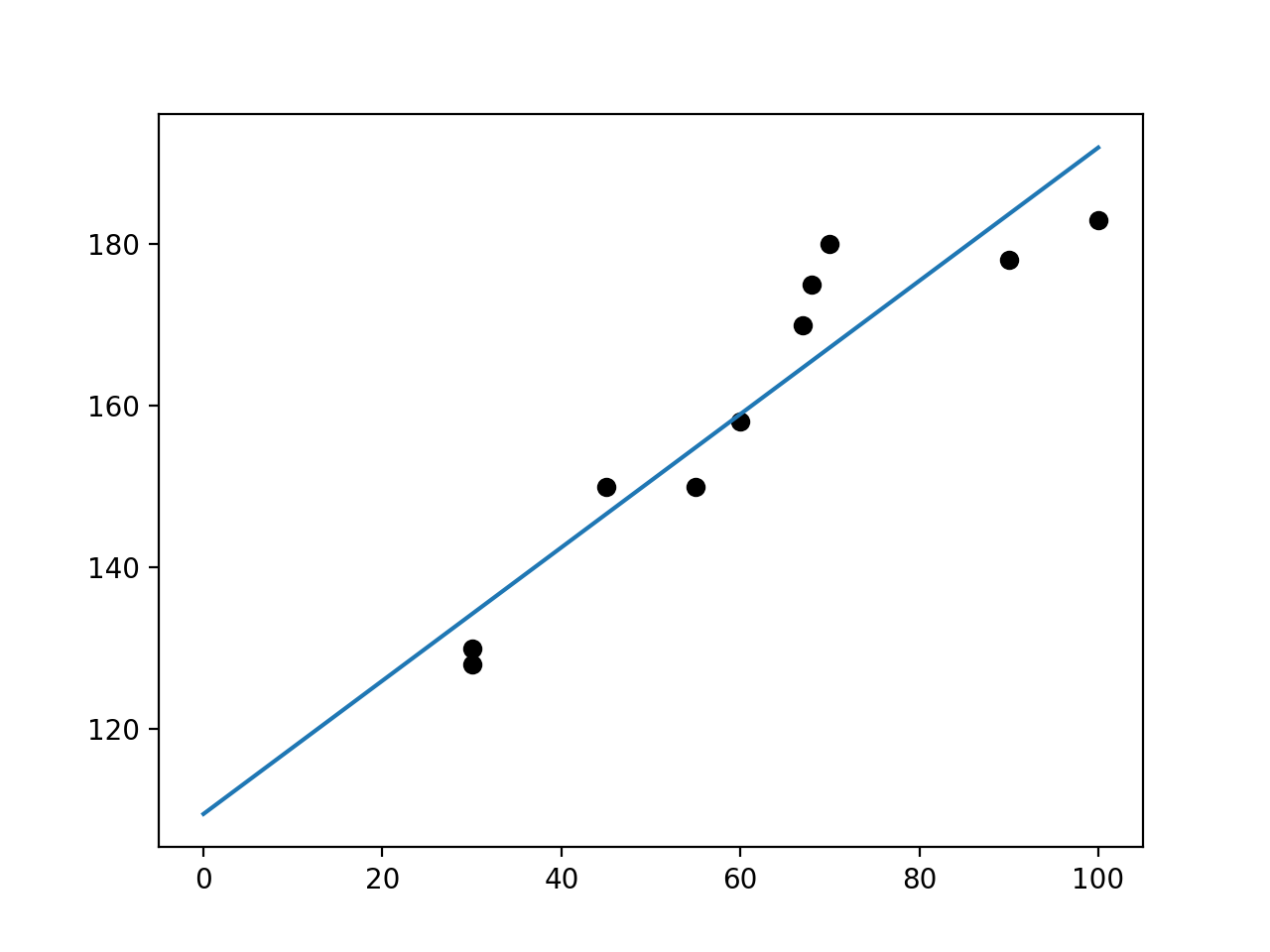
例えば体重からその人の身長を予測したい!!!ってなったとします。そのために10人分の体重と身長のデータを集めて以下のようないいかんじの直線を書くことをいいます。
数学的な説明をするとそれらしい直線とは以下のような形をしています。
$$\hat{y}=ax+b$$
$$\hat{y}:身長$$
$$x:体重$$
$$a:傾き(aには定数が入ります)$$
$$b:切片(a同様に定数が入ります)$$
上記の式のaとbを求めることを単回帰分析と言います。
yの上に^みたいなのがついていますがこれはハットといって予測値のyにつけるみたいです。
このaとbの求める方法として最小二乗法を使用します。重回帰分析の説明のときに最小二乗法の説明をしますのでここでは省略します。
また以下のurlで最小二乗法についてわかりやすく説明されている方がおられたのでそちらを参考にしていただいても構いません。
aとbを求めることができたらxに体重を代入すればy(身長)を予測することができます。
この例でできたやつたちの正式名称を次の重回帰分析の説明のために示しておきます。
-
体重:説明変数
-
身長:目的変数
今回の例では体重のデータを元に身長を予測しました。求めたい値を目的変数、求めたい値(目的変数)を予測するために使用する値を説明変数といいます。
-
体重のデータ(説明変数のデータ) が10個ありましたのでこれをサンプル数といいます。
-
単回帰分析とは説明変数1つで目的変数を予測する場合のことを単回帰分析といいます。
重回帰分析とは
複数の説明変数から目的変数を予測する回帰分析のことを重回帰分析といいます。
例としては・・・
先ほどの単回帰分析では体重のみから身長を予測していました。でも現実に置き換えて考えてみると体重だけから身長を予測することはなかなか難しそうですよねー。ガリガリの人もいればおデブな方もいるんで先ほどの単回帰分析では正確な身長を予測することは難しそう。
ではどうすればいいか
それは身長を予測するときに関係のありそうなウエストとか足のサイズとかも説明変数に使用すればもっと正確な予測ができるんじゃね❓って考えられたのが重回帰分析って感じです。
イメージできましたかね❓
ここからは少し数学的な話をしていきます。
重回帰分析の一般的な式は以下のような式となっています。
$$\hat{y}=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3+・・・+\beta_nx_n$$
$$\hat{y}:目的変数$$
$$\beta_0:バイアス$$
$$\beta_1,\beta_2,...,\beta_n:回帰係数$$
$$x_1,x_2,...x_n:説明変数$$
-
目的変数は単回帰分析のときと同じで予測値(身長)になります。
-
$\beta_0$はバイアスといって単回帰分析でいうb(切片)のようなものです。
-
回帰係数とは単回帰分析でいうa(傾き)のようなものです。重回帰分析は説明変数が複数あるためそれぞれの説明変数に応じた数のaを求めるようなイメージです。
-
説明変数は例でいくと体重、ウエスト、足のサイズの3つの説明変数があるので上記の式は以下のようになります。
$$\hat{y}=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3$$
これから求め方についての説明をしていきます。
わかりやすくするために以下の例で説明します。
【例】体重、ウエスト、足のサイズの3つの説明変数から身長(目的変数)を予測する。サンプル数は5する。
具体的にすると・・・
Aさん・・・体重:50kg、ウエスト:60cm、足のサイズ:23cm →身長:155cm
Bさん・・・体重:60kg、ウエスト:70cm、足のサイズ:25cm →身長:162cm
Cさん・・・体重:70kg、ウエスト:78cm、足のサイズ:27cm →身長:173cm
Dさん・・・体重:30kg、ウエスト:50cm、足のサイズ:19cm →身長:135cm
Eさん・・・体重:80kg、ウエスト:95cm、足のサイズ:27cm →身長:175cm
以上の計5人のデータからいい感じの回帰係数β1,β2,β3をみつけてを未知の人間の身長を予測できるようないい感じの関数($\hat{y}$)をつくることが目的です!
文字が多くなるので少し休憩してから読んでみてください。
まず手順としては、仮にいい感じの$\beta$を求めることができたときにそれが本当にいい感じなのか評価する必要があります。それを評価する方法として最小二乗法という方法があります。先ほどの単回帰分析のときurlを読まれた方は理解できたかもしれませんがここでも簡単に説明します。
最小二乗法とは・・・
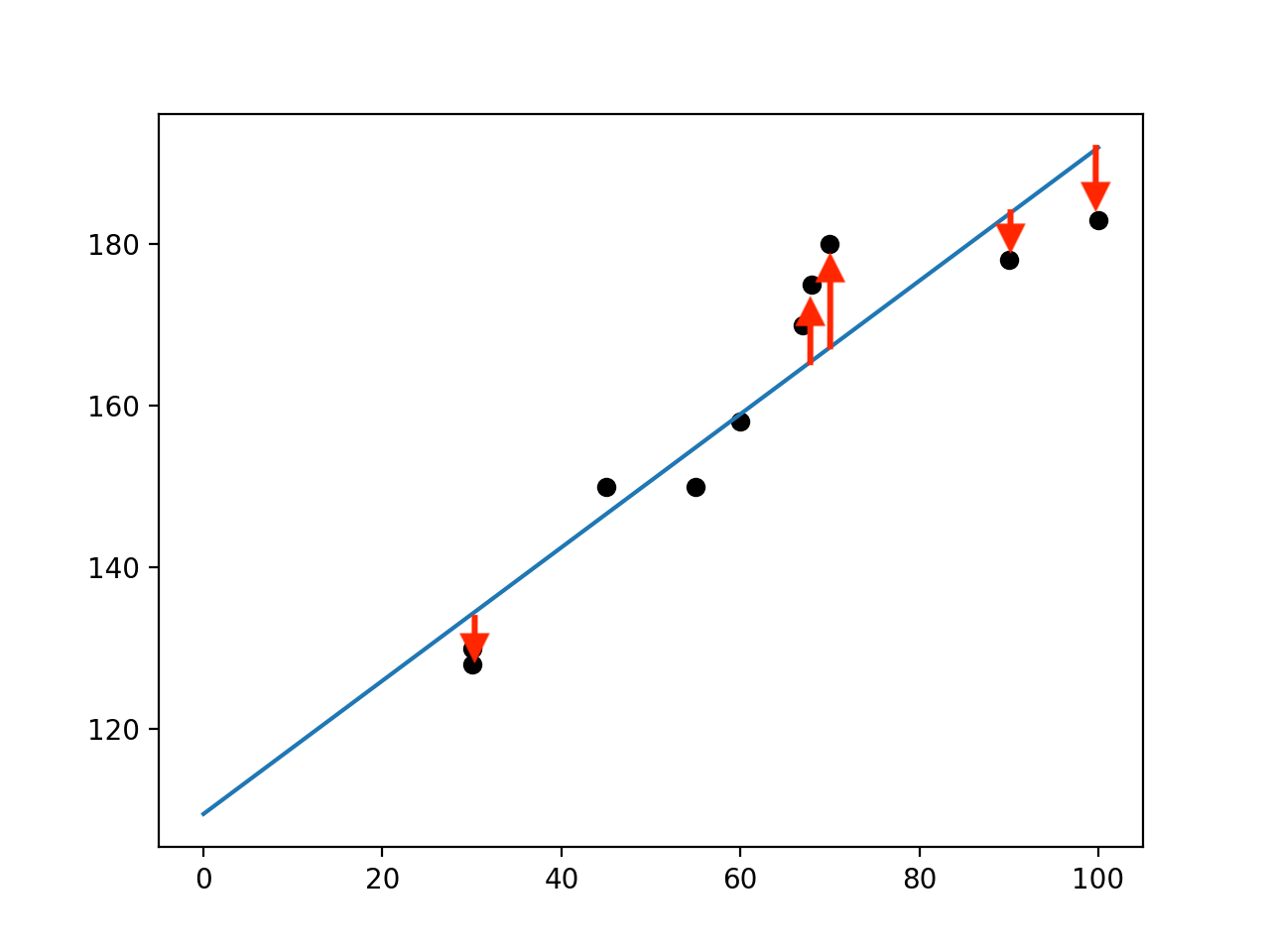
以下の画像のように何個かのデータからいい感じの線を引いたとします。するとそれぞれの点と線には誤差があります。(画像中の赤線が誤差です。)すべての点と線の誤差を足してその誤差の合計が小さいとその分だけいい感じの直線がひけた!ということになります。
ですが、誤差には線の下に点(誤差がマイナス)があったり、線の上に点(誤差がプラス)があったり符号が違うことがあります。そのまま誤差を足していくと、たまたまプラマイ0みたいな感じでホントは誤差が大きのに誤差が少ないと評価されてしまう可能せいがあります。それは避けたい。
とうことで符号を統一したい!
ということで符号を統一できるものとして考えられるのが、絶対値がありますが、絶対値は計算を場合分けしたりする必要がありとても扱いにくいので避けたい。
そのほかに同じ符号を消せる方法として考えられたのが誤差を2乗して符号を統一してしまう方法は・・・最小二乗法だ!となったわけです。
最小2乗法の一般式は以下のとおりです。
$$E(D)=\sum_{i=1}^{n} (y_i-\hat{y}_i)^2$$
今回の例でいくと・・・
$$E(D)=\sum_{i=1}^{n} (y_i-(\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3))^2$$
$$E(D):誤差関数$$
$$y_i:実際の身長データ$$
$$n:サンプル数$$
$$\hat{y}:目的変数$$
$$\beta_0:バイアス$$
$$\beta_1,\beta_2,\beta_3:回帰係数$$
$$x_1,x_2,x_3:説明変数$$
となります。
(補足)
$y_i$とは今回の例でいくとAからEさんまでの実際の身長のデータになります。
要はAさんからEさんの実際の身長と予測したAさんからEさんの身長の誤差を二乗して合計したものです。
$n$は今回の例だと5になります。
そしてこの誤差関数$E(D)$を最小にしたい!ということになります。
じゃあどうすればいいのか❓
最小とか最大にしたいとかそういうときにみなさんは何が思い浮かびますかね❓
微分して=0にすると最大値または最小値になるとか浮かんできませんかね-❓
私はなにも思い浮かびませんでした。
ということで、以下の手順が結論になります。
①
$\beta_0,\beta_1,\beta_2,\beta_3$で$E(D)$をそれぞれ偏微分します。以下みたいな記号のやつです。
$$\frac{\partial E(D)}{\partial \beta_i}=0$$
$$i=(0,1,2,3)$$
②
そして偏微分した左辺を0とします。偏微分したものを=0とすると傾きが0の地点すなわちE(D)が最小値となる箇所の各βを求めることができるため=0としています。ですがこの説明だけだと傾きが0の地点ということはE(D)が最小値ではなくて最大値になるんじゃない❓と思った方もいると思います。詳しい説明は省略しますが、上記のE(D)の式を$\beta_0$を固定してみると他の$\beta_1,\beta_2,\beta_3$の最高次数は2(2次関数)となり、かつ符号はプラスとなるため下に凸の二次関数となるため偏微分した後=0として求めらるのは最小値となります。ここに関してすごくわかりづらいと思うのでヨビノリ先生のわかりやすい動画のurlを載せておきます。
③
$\beta_0,\beta_1,\beta_2,\beta_3$それぞれで偏微分したので方程式が4つできます。
その連立方程式をがんばって解くと・・・
$E(D)$を最小にしてくれる$\beta_0,\beta_1,\beta_2,\beta_3$がそれぞれ求まる!って感じです。
上記の導出は今回の例は説明変数が3つですが、これがもっと増えても基本的に導出方法は同じで連立方程式を解くのが大変になるくらいの違いしかありません。
そして導出後の形は公式があります。(なので上記のめんどくさい導出はしなくてもいいです笑)それは以下のとおりです。
その前に説明していた計算を行列で表現する方法を説明しておきます。(導出後の公式は行列で表現してあるからです、。)
$$E(D)=\sum_{i=1}^{n} (y_i-(\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3))^2$$
そして上記の式を行列で表してみると・・・
$$E(D)=||y-X\beta||^2$$
|| ||の中を展開してみると・・・
\begin{align}
& = \left(
\begin{matrix}
y_0 \\
y_1 \\
y_2 \\
y_3 \\
y_4 \\
y_5 \\
\end{matrix}
\right)-
\left(
\begin{matrix}
1 & x_{11} & x_{12} & x_{13} \\
1 & x_{21} & x_{22} & x_{23} \\
1 & x_{31} & x_{32} & x_{33} \\
1 & x_{41} & x_{42} & x_{43} \\
1 & x_{51} & x_{52} & x_{53} \\
\end{matrix}
\right)
\left(
\begin{matrix}
\beta_0 \\
\beta_1 \\
\beta_2 \\
\beta_3
\end{matrix}
\right)\\
& =\left(
\begin{matrix}
y_0 \\
y_1 \\
y_2 \\
y_3 \\
y_4 \\
y_5 \\
\end{matrix}
\right)-
\left(
\begin{matrix}
\beta_0+\beta_1x_{11}+\beta_2x_{12}+\beta_3x_{13} \\
\beta_0+\beta_1x_{21}+\beta_2x_{22}+\beta_3x_{23} \\
\beta_0+\beta_1x_{31}+\beta_2x_{32}+\beta_3x_{33} \\
\beta_0+\beta_1x_{41}+\beta_2x_{42}+\beta_3x_{43} \\
\beta_0+\beta_1x_{51}+\beta_2x_{52}+\beta_3x_{53} \\
\end{matrix}
\right)
\end{align}
となりきちんと$E(D)$と同じ形になっているのがわかります。
上記の式の各成分を行列で表すとこんな感じになります。
\beta = \left(
\begin{matrix}
\beta_0 \\
\beta_1 \\
\beta_2 \\
\beta_3
\end{matrix}
\right)
y = \left(
\begin{matrix}
y_0 \\
y_1 \\
y_2 \\
y_3 \\
y_4 \\
y_5 \\
\end{matrix}
\right)
X = \left(
\begin{matrix}
1 & x_{11} & x_{12} & x_{13} \\
1 & x_{21} & x_{22} & x_{23} \\
1 & x_{31} & x_{32} & x_{33} \\
1 & x_{41} & x_{42} & x_{43} \\
1 & x_{51} & x_{52} & x_{53} \\
\end{matrix}
\right)
いきなりこんなこと言われても全然意味がわかりませんよね。
ひとつずつ説明していきます。
$\beta$:これはいい感じの線を引くために最終的に求めたい値でした。その数は説明変数の数+1(バイアス)ですので今回の例でいくと4つあるものを列表記したものです。
$y$:これは上からサンプルとして与えられたAさんからEさんまでの身長のデータですので5つあるものを列表記したものです。
$X$:これが一番分からなかったと思います。1列目は全部1になっています。これはバイアスには何もかける必要がないから1かけとこかーって感じ1列目は全部1になっています。上記の展開した式をみると1列目の1があることによってちゃんとなっているのがわかると思います。(他の文献ではバイアスは別で求めており1列目に1のみの列がないこともあります。)
2列目は上からAさんからEさんの体重データです。
3列目は上からAさんからEさんのウエストデータです。
4列目は上からAさんからEさんの足のサイズのデータです。
行数はサンプル数、列数は求めるβの数(説明変数+1)となっています。
例えば$x_{23}$の場合はBさんの足のサイズの25cmが入ることになります。
これで行列での表現の仕方はなんとなくわかったと思いますので、$\beta$を求める公式をお伝えします。
$$\beta = (X^TX)^{-1}X^Ty$$
これです。ピンとこないかもしれませんがこれです笑 $X^T$っていうのは$X$の転置行列のことです。転置行列とは行と列を入れ替えたものです。
それでは実際に公式を使用して求めてみましょう。
例のデータを再度記載しておきます。
Aさん・・・体重:50kg、ウエスト:60cm、足のサイズ:23cm →身長:155cm
Bさん・・・体重:60kg、ウエスト:70cm、足のサイズ:25cm →身長:162cm
Cさん・・・体重:70kg、ウエスト:78cm、足のサイズ:27cm →身長:173cm
Dさん・・・体重:30kg、ウエスト:50cm、足のサイズ:19cm →身長:135cm
Eさん・・・体重:80kg、ウエスト:95cm、足のサイズ:27cm →身長:175cm
なお以下のプログラムの一部は以下のurlを参考にしました。
以下のプログラムでは公式を使って回帰係数を求めて、[体重:80kg,ウエスト:90cm,足のサイズ:27cm] の人の身長を予測しています。
【5分でわかる】重回帰分析を簡単解説【例題付き】
# coding=utf-8
# 重回帰分析
def Multiple_regression(X, y):
# 偏回帰係数ベクトル
A = np.dot(X.T, X) # X^T*X
A_inv = np.linalg.inv(A) # (X^T*X)^(-1)
B = np.dot(X.T, y) # X^T*y
beta = np.dot(A_inv, B)
return beta
# 説明変数行列(体重、ウエスト、足のサイズ)
X = np.array([[1, 50, 60, 23], [1, 60, 70, 25], [
1, 70, 78, 27], [1, 30, 50, 19], [1, 80, 95, 27]])
# 目的変数ベクトル(身長)
y = np.array([[155], [162], [173], [135], [175]])
# 偏回帰係数ベクトル
beta = Multiple_regression(X, y)
print(beta)
predict_data = [1, 80, 90, 27] # 予測したいデータ
def predict(beta, predict_data):
# 実際の予測の計算
predict_tall = beta[0] * predict_data[0] + beta[1] * predict_data[1] + \
beta[2] * predict_data[2] + beta[3] * predict_data[3]
return predict_tall
tall = predict(beta, predict_data)
print(tall)
得られた結果は以下のとおりです。
β = [[90.85638298]
[ 0.76276596]
[-0.28723404]
[ 1.86702128]]
予測身長(体重:80kg,ウエスト:90cm,足のサイズ:27cmの人間)
y = 176.43617021cm
βは上から$\beta_0,\beta_1,\beta_2,\beta_3$となっています。
それを以下の式に当てはめて計算すると・・・
$$\hat{y}=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3$$
$$\hat{y}=90.85638298+0.76276596 × 80 - 0.28723404 × 90 + 1.86702128 × 27 = 176.43617021$$
176cmと予測することができました。なんとなくいい感じの予測にはなってそうですよね。
以上一通りの説明は終わりです。たいへんお疲れ様でした。
重回帰分析についてなんとなくでも理解ができたでしょうかねー。雰囲気だけでもわかっていただけたら幸いです。
今回話をまとめると・・・
○重回帰分析は単回帰分析のパワーアップしたやつで複数の説明変数から目的変数を予測できるやつ
○重回帰分析は最適な回帰係数を求めるこが一番大事。そこで使用するのが最小二乗法!
$$E(D)=\sum_{i=1}^{n} (y_i-(\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3))^2$$
E(D)誤差関数が最小になる回帰係数を求める。偏微分したりしてがんばると以下の公式が得られる。
$$\beta = (X^TX)^{-1}X^Ty$$
あと少しだけ今回の例以外で重回帰分析についての補足をしておきます。
補足
○グラフに図示できる重回帰分析は説明変数が2つまでです。X軸、y軸、Z軸までしか図示できないためです。
それ以上は想像の世界になりますが考え方は基本的に単回帰分析と同じです。
○今回はいい感じの直線を引くことによって身長を予測していましたが、世の中には直線では表現できないものを存在します。
X = \left(
\begin{matrix}
1 & x_{11} & x_{12} & x_{13} \\
1 & x_{21} & x_{22} & x_{23} \\
1 & x_{31} & x_{32} & x_{33} \\
1 & x_{41} & x_{42} & x_{43} \\
1 & x_{51} & x_{52} & x_{53} \\
\end{matrix}
\right)
今回は説明変数を単純な一次の関数を使用して予測していたため予測線が直線になっていました。
ですが重回帰分析では非線型(直線ではない形、曲線)の予測線を描きたいときもあります。そんなときは説明変数の行列の関数を2次、3次にしたりして表現することがあるらしいです。
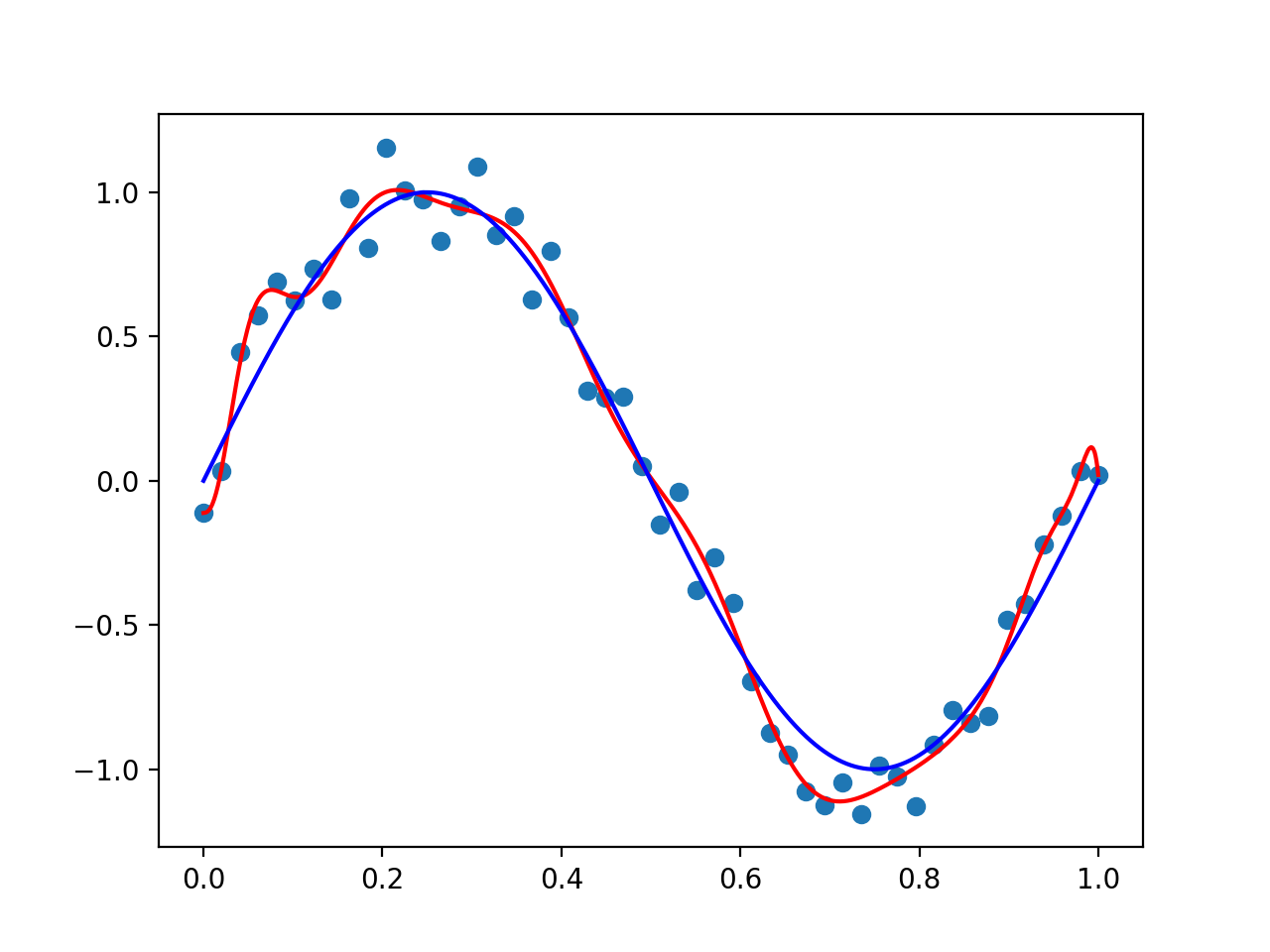
実際に曲線の予測をすると次は過学習といった問題も発生してきます。過学習とは与えられたデータに対して過剰にフィットしすぎてしまいきちんとした予測を行えない予測線になっていることをいいます。イメージは以下の画像みてください。
(画像の説明)
薄い青色の点々が与えられたデータ群
実際に引きたい予測線は青色の線
赤色の線が過学習を起こして、与えられたデータ群に過剰にフィットしている。
このように曲線にしたらしたで過学習という問題が発生します。それを防ぐために正則化という方法を使用するらしいです。ですので次回は正則化についてまとめていこうと思います。記事ができましたらこの下に貼っておきますのでぜひ確認してみてください。