ジャンプを実装するとき,重力をイメージして放物軌道を作りがちです.
だがHAL研の方はかく語りき.
キャラクターを動かすプログラムでは、ときに自然法則を無視して気持ちよさを追求する、ということをよく行います。
自然界の物理法則よりも気持ちいいジャンプ,探求したいと思いませんか?
この記事ではジャンプの実装方法をいくつか紹介します.結局重力使えばいいやと思わなくもないですが…
初めに
今回はヒヨコ🐤ちゃんがジャンプします!以下ヒヨコちゃんの座標は $(x, y)$ と表記します.ただし画面左上が原点で,画面下方向にyの値が増えていくことに注意です.この辺は使用したゲームエンジン pyxel の仕様です.(あとクラスで書いてないので,邪悪なグローバル変数だらけです….先に謝ります)
最初に実装の全体像を示します.
import pyxel
def drawHiyoko(x, y):
# ヒヨコを (x, y) に描画する
pyxel.blt(x, y, 0, 16, 16, 16, 16, pyxel.COLOR_LIGHTGRAY)
Y_GROUND = 100 # 地面のy座標
canJump = True # ジャンプ可能かどうか(=地面にいるかどうか)
x, y = 54, Y_GROUND # ヒヨコの座標
# この記事では以下の二つをいろいろ実装してみます
def jump():
# TODO: canJumpフラグをオフにする
def hiyoko_update():
# TODO: ヒヨコの座標の更新
# ===== main =====
pyxel.init(125, 125) # 125x125 の画面を作成
pyxel.load('assets/piyo.pyxres') # アセット
while True:
pyxel.cls(col=pyxel.COLOR_WHITE) # 白い背景
pyxel.line(0, Y_GROUND+16,
pyxel.width, Y_GROUND+16, pyxel.COLOR_BROWN) # 地面の描画
if pyxel.btn(pyxel.KEY_SPACE): # space でジャンプ
jump()
hiyoko_update()
drawHiyoko(x, y)
pyxel.flip()
spaceキーを押したら,ヒヨコがジャンプするだけのものです.以後 jump() と hiyoko_update() を中心にみていきます.
まずは自然法則から
①座標・速度・加速度を保持するやり方
一番有名なやり方から見てみましょう.
ヒヨコのy座標,y方向の速度,y方向の加速度を保持して,毎フレーム更新するやり方です.
- 速度 = 座標の単位時間当たりの変化量
- 加速度 = 速度の単位時間当たりの変化量
というイメージで実装します.地面にいるときは $速度=0$ で,ジャンプする時に $速度=-10$ のように初速度を与えてあげます.ジャンプ中は毎回速度と座標を更新していき,ひよこが地面についたらそこで(ジャンプ可能フラグ)をオンに戻します.
vel = 0 # y方向の速度
acc = 1 # 重力加速度
def jump():
global canJump, vel
if canJump:
canJump = False
time = 0
vel = -10 # 初速を与える
def hiyoko_update():
global acc, vel, y, canJump
if canJump:
return
# 更新
vel += acc
y += vel
if y > Y_GROUND: # 地面についたら
y = Y_GROUND
vel = 0
canJump = True
よくあるやつや!
➁公式を使う
上方向への放物軌道は次の式にです(鉛直投げ上げの式)
y = v_0t - \dfrac{1}{2}gt^2 + y_\text{ground} \qquad (y_\text{ground} \text{は地面の高さ})
ここで$v_0$は初速度,$g$は重力加速度です.これを素直に実装してみます.条件をそろえればさっきと同じです.
v0 = 9 # 初速度
time = 0 # 時間
gravity= 0.9 # 重力加速度
def jump():
global canJump, time
if canJump:
canJump = False
time = 0
def hiyoko_update():
global gravity, time, v0, x, y, canJump
if canJump:
return
y = 0.5*gravity*time*time - v0*time + HORIZONTAL_Y
if y > HORIZONTAL_Y: # 地面についたら
y = HORIZONTAL_Y
canJump = True
time += 1
重力加速度や初速を変えるとジャンプの高さや速度を変えることができます.↑は宇宙みたいなジャンプです!
よくある実装で重力も高さも変えられるんですが,滞空時間やジャンプの高さを決めてから初速を計算するのはめんどくさかったりします.
\begin{align*}
(滞空時間) &= \frac{2v_0}{g} \\[8pt]
(ジャンプの高さ) &= \frac{v_0^2}{2g}
\end{align*}
上の式から初速を逆算できます
➂三角関数 sin を使う
$\sin \theta$ カーブも定義域 $\theta \in [0, \pi]$ で放物軌道みたいな形なので使えそうです.
実装したらこんな感じ(上のコードと違う部分だけ書いてます)
radPerFrame = 2*pi/40 # radian per frame
height = 45 # height of jump
frames = 0 # framecount while jumping
def jump():
global canJump, frames
if canJump:
canJump = False
frames = 0
def hiyoko_update():
global frames, y, canJump
if canJump: # if hiyoko on the ground
return
y = - height * sin(radPerFrame*frames) + Y_GROUND
frames += 1
if y > Y_GROUND: # when hiyoko get on the ground
y = Y_GROUND
canJump = True
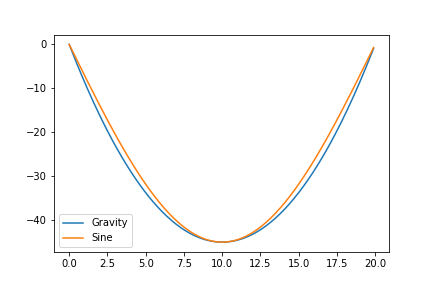
高さと滞空時間をそろえて比較してみました.チガイワカラナイ.高さと滞空時間を変更しやすいので,sin で実装するのは割とよさそうです.
④三角関数を応用する
三角関数では簡単にジャンプの高さと滞空時間を調整できて便利でした.これに加えて軌道のゆがみ(distortion)も調節できたら便利そうです.HAL研のブログに面白いのが載っていました.
y = \text{height} \times (1 - (1 - \sin \pi t)^\text{distortion})
式の意味は Melville (@V_Melville) さんの説明がわかりよいです.
sinを1に近いときだけ1に近づけようとするとこうなると思います(そういう話ではないですか?) pic.twitter.com/eVnY5dvsVm
— Melville (@V_Melville) September 1, 2019
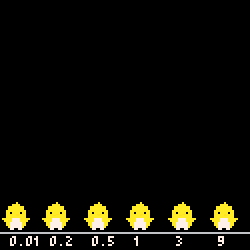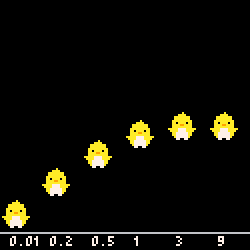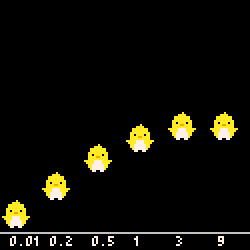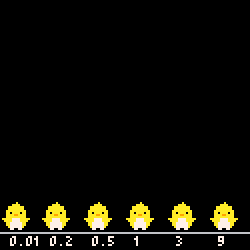
さっそく $\text{distortion}$ の値をいじってみると…
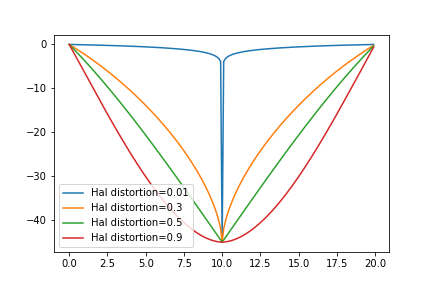
$\text{distortion} < 1$ では
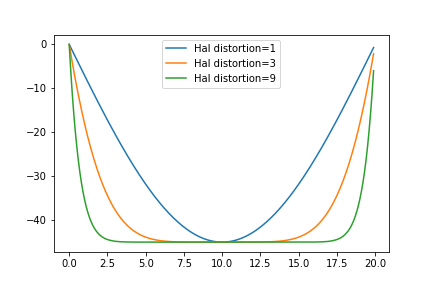
$\text{distortion} > 1$ では
まとめると…
- $\text{distortion} = 0.01$ :インパルス関数的な動き
- $\text{distortion} = 0.5$ :等速っぽい往復(違うけど)
- $\text{distortion} = 1$ :$\sin \pi t$
- $\text{distortion} = 3$ :キュッと上がってキュッと下がる
- $\text{distortion} \rightarrow \infty $ :$y = \text{height}$ で動かない
おおお!!
値を調節すればメリハリのある動きが作れそうです!(両端はかなり極端ですが)
実装例は以下.
t = 0 # from 0 to 1
distortion = 3 # ゆがみ
height = 45 # height of jump
def jump():
global canJump, t
if canJump:
canJump = False
t = 0
def hiyoko_update():
global t, y, canJump
if canJump: # if hiyoko is on the ground
return
if t>1: # if hiyoko get on the ground
canJump = True
t = 0
y = Y_GROUND
return
t += 1/60
y = Y_GrOUND - (1.0 - pow(1.0-sin(pi*t), distortion))*height
非対称なジャンプ
ここまでの実装ではそのまま書くと,上昇時と下降時で対称性のある動きをします.重力加速度を二つ用意したり場合分けするのも一案ですが,せっかくなので関数を試してみます.
⑤log関数
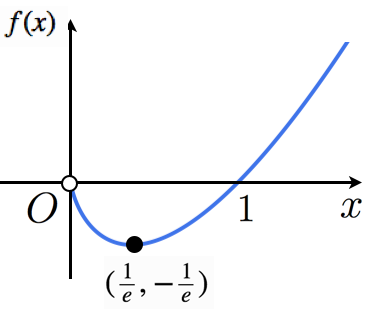
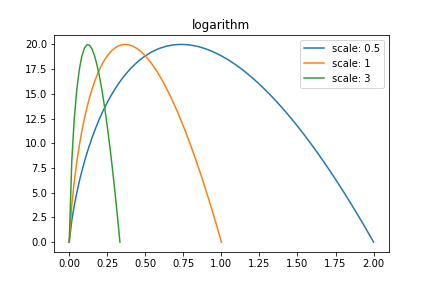
なんとなく $\log$ とかよさそうな気がします.$y = x \log x$ の概形は以下.(高校数学の美しい物語 より)
よって高さを $\text{height}$ にしたい場合は $y = \text{height} \times e \times x \log x$ とすればよさそうです.あとジャンプの滞空時間も制御したいので,$y = (x \times \text{scale}) \log(x \times \text{scale})$ とでもしときます.
上昇に比べて下降が少しゆっくりな感じになりました.(結局重力加速度を二つ用意したほうが調整しやすそうではある)
おまけ(⑥マリオ)
色々調べてたらこんなの見つけました!
マリオの速度ベクトルを保存しておいて座標を計算するんじゃなくて、
マリオの前回の座標を保存しておいて座標を計算しているんだそうです。y_temp = Mario.y; Mario.y += (Mario.y - Mario.y_prev) + F; Mario.y_prev = y_temp;Fはその瞬間の力で、ジャンプの瞬間はF=10にして、空中ではF=-1にします。
するとこんな放物線になります。
[0,10,19, 27, 34, 40, 45, 49, 52, 54, 55, 55, 54, 52, 49, 45, 40, 34, 27, 19, 10, 0]加減算しか使わないので、非常に高速にできたと。
①の速度ベクトルを保存するやり方ではなく,前フレームの座標の保存だけで次フレームの座標が決まります.$y - y_{prev}$ で座標の差分(速度)が出るので,確かに放物軌道になりそうです.マリオで使われていた?やり方らしいです.
y_prev = y # 1フレーム前の y
F = -1 # ジャンプの瞬間だけ -10, 他は -1
def jump():
global canJump, F
if canJump:
F = -10 # ジャンプの瞬間だけ -10
canJump = False
def hiyoko_update():
global x, y, y_prev, F, canJump
if canJump:
return
y_tmp = y
y += (y - y_prev) + F # ココがミソ
y_prev = y_tmp
F = 1
if y == Y_GROUND:
canJump = True
普通に放物軌道でジャンプしてますね.おもしろいです!
さいごに
他の実装方法などご存じでしたら教えてほしいです!説明が間違っているなども指摘してもらえると助かります
m(__)m
参考リンク
マリオのジャンプ実装法とVerlet積分(Gemmaの日記)