【Sympy演算処理】線形代数再入門①「複式簿記」から「単位行列=単位ベクトル」へ。

連立一次方程式も行列演算も、それ自体はコンピューターに丸投げすれば一瞬で解いてくれます。むしろその時何が起こってるかちゃんとイメージするのが難しいという…

1.行列演算の出発点としての「複式簿記」。

【Python演算処理】行列演算の基本④大源流における記述統計学との密接な関連性?
「とある喫茶店におけるコーヒーと紅茶の1週間の売り上げ」から出発。

	Coffe	Tea	Total
0	18	10	8900
1	4	5	2950
2	41	6	14400
3	49	23	22750
4	4	9	4350
5	41	6	14400
6	33	35	22150

①これをそのまま行列表現したのが拡大係数行列(Augmented Coefficient Matrix)」となる。

import sympy as sp
import numpy as np
import pandas as pd
a,b,x,y = sp.symbols('a,b,x,y')
A = sp.Matrix([[300,350]])
X = sp.Matrix([[18,4,41,49,4,41,33],[10,5,6,23,9,6,35]])
X1=X.row_insert(2, A*X)
x=X1.transpose()
df=pd.DataFrame(np.matrix(x),columns=['Coffe', 'Tea', 'Total'])
sp.init_printing()
display(A)
display(X) 
display(A*X)
print(sp.latex(Aa)+sp.latex(X)+"="+sp.latex(Aa*X))
display(x)
org=df.to_html()
print(org.replace('\n', ''))

\left[\begin{matrix}18 & 10 & 8900\\4 & 5 & 2950\\41 & 6 & 14400\\49 & 23 & 22750\\4 & 9 & 4350\\41 & 6 & 14400\\33 & 35 & 22150\end{matrix}\right]

②ここでコーヒーの単価は300円、紅茶は350円。毎日の売り上げを行列演算結果に対応させると以下となる。

import sympy as sp
a,b,x,y = sp.symbols('a,b,x,y')
A = sp.Matrix([[a,b]])
X = sp.Matrix([[x],[y]])
AX=A*X
expr00 =AX[0]
Aa=A.subs([(a,300),(b,350)])
Xr=sp.randMatrix(2,7, min=0, max=50)
sp.init_printing()
display(Aa)
display(X) 
display(Aa*X)
print(sp.latex(Aa)+sp.latex(X)+"="+sp.latex(Aa*X))
display(Xr) 
display(Aa*Xr)
print(sp.latex(Aa)+sp.latex(Xr)+"="+sp.latex(Aa*Xr))

\left[\begin{matrix}300 & 350\end{matrix}\right]\left[\begin{matrix}x\\y\end{matrix}\right]=\left[\begin{matrix}300 x + 350 y\end{matrix}\right] \\
\left[\begin{matrix}300 & 350\end{matrix}\right]\left[\begin{matrix}18 & 4 & 41 & 49 & 4 & 41 & 33\\10 & 5 & 6 & 23 & 9 & 6 & 35\end{matrix}\right]=\left[\begin{matrix}8900 & 2950 & 14400 & 22750 & 4350 & 14400 & 22150\end{matrix}\right]

③ここから複式簿記(Double-entry bookkeeping)と一次方程式(Linear Equation)と行列演算(Matrix Operation)の関係が浮かび上がってくる。

import sympy as sp
a,b,c,x,y = sp.symbols('a,b,c,x,y')
A = sp.Matrix([[a,b,c]])
X = sp.Matrix([[x],[y],[-1]])
AX=A*X
expr00 =AX[0]
expr01 = sp.solve(expr00,y)
expr02 = sp.solve(expr00,x)
expr03 = sp.solve(expr00,c)
Aa=A.subs([(a,300),(b,350)])
expr00a = expr00.subs([(a,300),(b,350)])
expr01a = expr01[0].subs([(a,300),(b,350)])
expr02a = expr02[0].subs([(a,300),(b,350)])
expr03a = expr03[0].subs([(a,300),(b,350)])
sp.init_printing()
display(Aa)
display(X) 
display(Aa*X)
print(sp.latex(Aa)+sp.latex(X)+"="+sp.latex(Aa*X))
display(expr00a)
print(sp.latex(expr00a)+"=0")
display(expr01a)
print("y="+sp.latex(expr01a))
display(expr02a)
print("x="+sp.latex(expr02a))
display(expr03a)
print(sp.latex(expr03a)+"=c")

\left[\begin{matrix}300 & 350 & c\end{matrix}\right]\left[\begin{matrix}x\\y\\-1\end{matrix}\right]=\left[\begin{matrix}- c + 300 x + 350 y\end{matrix}\right] \\
- c + 300 x + 350 y=0 \\
y=\frac{c}{350} - \frac{6 x}{7} \\
x=\frac{c}{300} - \frac{7 y}{6} \\
300 x + 350 y=c

(拡大係数行列の部分集合として現れる)連立一次方程式の係数を並べた係数行列(Coefficient Matrix)を小行列(Minor Determinant)と呼びます。それは(自分自身との直積としての)正方行列(Square Matrix=列数と行数が等しい行列)を構成し、単位行列(Identity Matrix)」と呼ばれたりもする訳ですね。それが複式簿記でいうと適切な個数の売り上げデータからの逆算で単価表を作成する事に対応する訳です。

\left[\begin{matrix}1 & 0 & 300\\0 & 1 & 350\\300 & 350 & -\end{matrix}\right]

この様に連立一次方程式や行列演算を解くとは、まさに対角成分(Diagonal Element)のみを抽出しそれを求める過程に他なりません。ちなみに残りを非対角成分(Nondiagonal Element)と呼びます。成分(Elemennt)も元(Elemennt)も英語では同じ言葉。要するに数学ではこれらを同じ集合論上の概念として扱うのです。

2.連立一次方程式と行列演算の関係

行列の定義と演算規則

①Sympyで連立一次方程式を解く

import sympy as sp
a,b,c,d,e,f,x,y = sp.symbols('a,b,c,d,e,f,x,y')
eq1=sp.Eq(a*x+b*y, e)
eq2=sp.Eq(c*x+d*y, f)
expr01 =sp.solve ([eq1, eq2], [x, y]) 
#表示
sp.init_printing()
display(eq1)
display(eq2) 
display(expr01)
print(sp.latex(expr01))

a x + b y = e\\
c x + d y = f\\
\left\{ x : \frac{- b f + d e}{a d - b c}, \  y : \frac{a f - c e}{a d - b c}\right\}

ここで分母に現れるad-bcを行列式(Determinant)といい、その解が0になる時2式は単なる比例関係を表すだけとなって解が無数に存在する事になり(不定)、マイナスになる時は解が「反転」します。そして計算上矛盾が生じる時、解は存在しません(不能)。

「不定」の例(比例式が答えとなる)

import sympy as sp
a,b,c,d,e,f,x,y = sp.symbols('a,b,c,d,e,f,x,y')
eq10=sp.Eq(a*x+b*y, e)
eq20=sp.Eq(c*x+d*y, f)
#代入
eq11=eq10.subs(([(a, 1), (b, -2),(e,3)]))
eq21=eq20.subs(([(c, 3), (d, -6),(f,9)]))
#解法
expr01 =sp.solve ([eq11, eq21], [x, y]) 
#表示
sp.init_printing()
display(eq11)
display(eq21) 
display(expr01)
print(sp.latex(expr01))

x - 2 y = 3\\
3 x - 6 y = 9\\
\left\{ x : 2 y + 3\right\}

「不能」の例(空集合[]が答えとなる)

import sympy as sp
a,b,c,d,e,f,x,y = sp.symbols('a,b,c,d,e,f,x,y')
eq10=sp.Eq(a*x+b*y, e)
eq20=sp.Eq(c*x+d*y, f)
#代入
eq11=eq10.subs(([(a, 1), (b, -2),(e,3)]))
eq21=eq20.subs(([(c, 3), (d, -6),(f,10)]))
#解法
expr01 =sp.solve ([eq11, eq21], [x, y]) 
#表示
sp.init_printing()
display(eq11)
display(eq21) 
display(expr01)
print(sp.latex(expr01))

x - 2 y = 3\\
3 x - 6 y = 10\\
\left[ \right]

②行列演算との対応

import sympy as sp
a,b,c,d,x,y = sp.symbols('a,b,c,d,x,y')
mt1= sp.Matrix([[a,b],[c,d]])
mt2= sp.Matrix([[x],[y]])
expr01 =mt1*mt2 
#表示
sp.init_printing()
display(mt1)
display(mt2) 
display(expr01)
print(sp.latex(mt1)+sp.latex(mt2)+"="+sp.latex(expr01))

\left[\begin{matrix}a & b\\c & d\end{matrix}\right]\left[\begin{matrix}x\\y\end{matrix}\right]=\left[\begin{matrix}a x + b y\\c x + d y\end{matrix}\right]

ここから単位行列に到達する為に「現在の係数行列にそれを掛けると単位行列となる」逆行列(Inverse Matrix)の概念を導入。多くの線形代数入門書ではここで最初の難所を迎えるが「面倒な計算はコンピューターに丸投げする」式の考え方ではどうという事もない。

import sympy as sp
a,b,c,d,x,y = sp.symbols('a,b,c,d,x,y')
mt1= sp.Matrix([[a,b],[c,d]])
mt2= sp.Matrix([[x],[y]])
expr01 =mt1**(-1)
#表示
sp.init_printing()
display(mt1)
display(expr01)
print(sp.latex(mt1)+"^{-1}="+sp.latex(expr01))

\left[\begin{matrix}a & b\\c & d\end{matrix}\right]^{-1}=\left[\begin{matrix}\frac{d}{a d - b c} & - \frac{b}{a d - b c}\\- \frac{c}{a d - b c} & \frac{a}{a d - b c}\end{matrix}\right]

上掲の2つの式を合算すると同じ答えに到達する。

import sympy as sp
a,b,c,d,x,y = sp.symbols('a,b,c,d,x,y')
mt1= sp.Matrix([[a,b],[c,d]])
mt2= sp.Matrix([[x],[y]])
expr01 =mt1**(-1)*mt2
#表示
sp.init_printing()
display(mt1)
display(expr01)
print(sp.latex(mt1)+"^{-1}"+sp.latex(mt2)+"="+sp.latex(expr01))

\left[\begin{matrix}a & b\\c & d\end{matrix}\right]^{-1}\left[\begin{matrix}x\\y\end{matrix}\right]=\left[\begin{matrix}- \frac{b y}{a d - b c} + \frac{d x}{a d - b c}\\\frac{a y}{a d - b c} - \frac{c x}{a d - b c}\end{matrix}\right]

③「面倒な計算はコンピューターに丸投げする」式の考え方では計算が合うかだけが重要。そして実際、上述の式に具体的に同じ数値を代入すると、確かに計算結果が一致する。

• 連立一次方程式の場合

import sympy as sp
a,b,c,d,e,f,x,y = sp.symbols('a,b,c,d,e,f,x,y')
eq10=sp.Eq(a*x+b*y, e)
eq20=sp.Eq(c*x+d*y, f)
#代入
eq11=eq10.subs(([(a, 5), (b, -1),(e,9)]))
eq21=eq20.subs(([(c, 2), (d, 3),(f,7)]))
#解法
expr01 =sp.solve ([eq11, eq21], [x, y]) 
#表示
sp.init_printing()
display(eq11)
display(eq21) 
display(expr01)
print(sp.latex(expr01))

5 x - y = 9\\
2 x + 3 y = 7\\
\left\{ x : 2, \  y : 1\right\}

• 行列演算の場合

import sympy as sp
a,b,c,d,x,y = sp.symbols('a,b,c,d,x,y')
mt10= sp.Matrix([[a,b],[c,d]])
mt20= sp.Matrix([[x],[y]])
mt11=mt10.subs(([(a, 5), (b, -1),(c, 2), (d, 3)]))
mt21=mt20.subs(([(x,9),(y,7)]))
expr00=mt11**(-1)
expr01 =mt11**(-1)*mt21
#表示
sp.init_printing()
display(mt11)
display(mt21)
display(expr00)
print(sp.latex(mt11)+"^{-1}"+"="+sp.latex(expr00))
display(expr01)
print(sp.latex(mt11)+"^{-1}"+sp.latex(mt21)+"="+sp.latex(expr01))

\left[\begin{matrix}5 & -1\\2 & 3\end{matrix}\right]^{-1}=\left[\begin{matrix}\frac{3}{17} & \frac{1}{17}\\- \frac{2}{17} & \frac{5}{17}\end{matrix}\right]\\
\left[\begin{matrix}5 & -1\\2 & 3\end{matrix}\right]^{-1}\left[\begin{matrix}9\\7\end{matrix}\right]=\left[\begin{matrix}2\\1\end{matrix}\right]

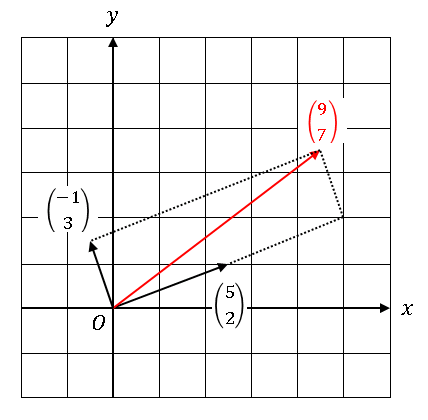
ところで上掲の状況は以下の様に基底の線形結合に変形する事も出来て、そしてこの形だと行列/ベクトル演算における基底のスカラー倍(この例ではx成分が2倍、y成分が1倍)を説明するのです。

\left[\begin{matrix}5 & -1\\2 & 3\end{matrix}\right]\left[\begin{matrix}x\\y\end{matrix}\right]=\left[\begin{matrix}5 x - y\\2 x + 3 y\end{matrix}\right]=x\left[\begin{matrix}5\\2\end{matrix}\right]+y\left[\begin{matrix}-1\\3\end{matrix}\right]

数学的構造(Mathematical Structure)の概念って、こんな思わぬ形で人間が普段使いしている多種多様な諸概念を貫いていたりするんですね。
【用語集】ユージン・ウィグナー『自然科学における数学の理不尽なまでの有効性(1959年)』
そんな感じで以下続報…