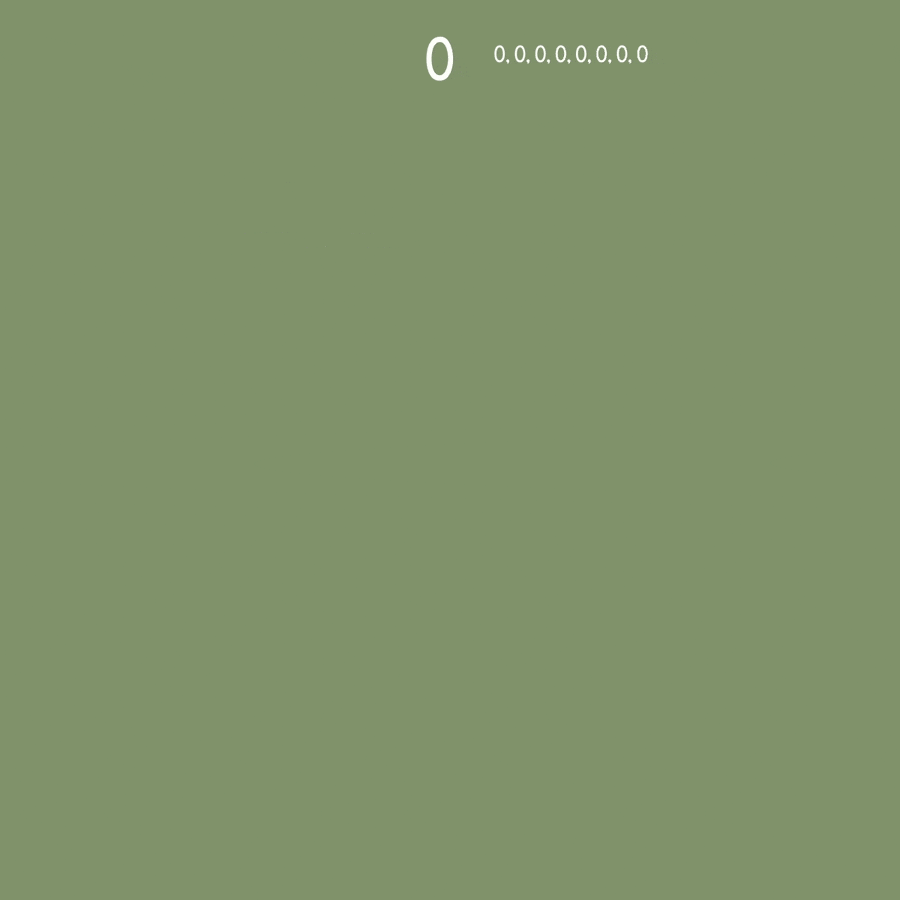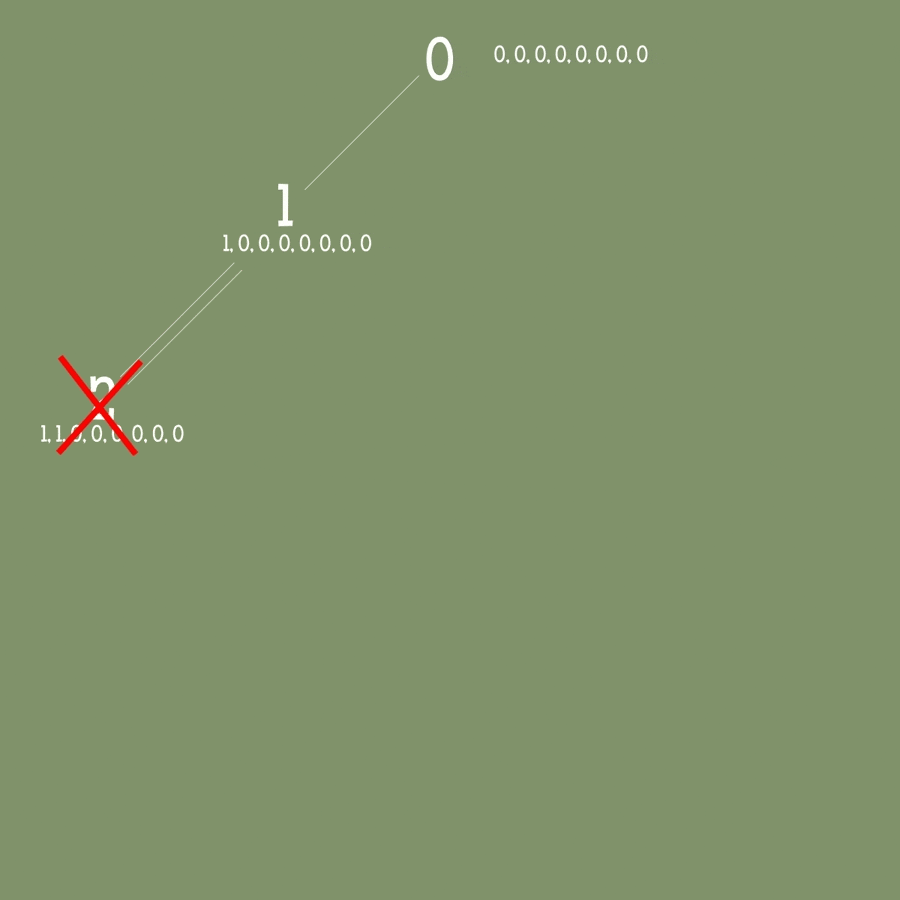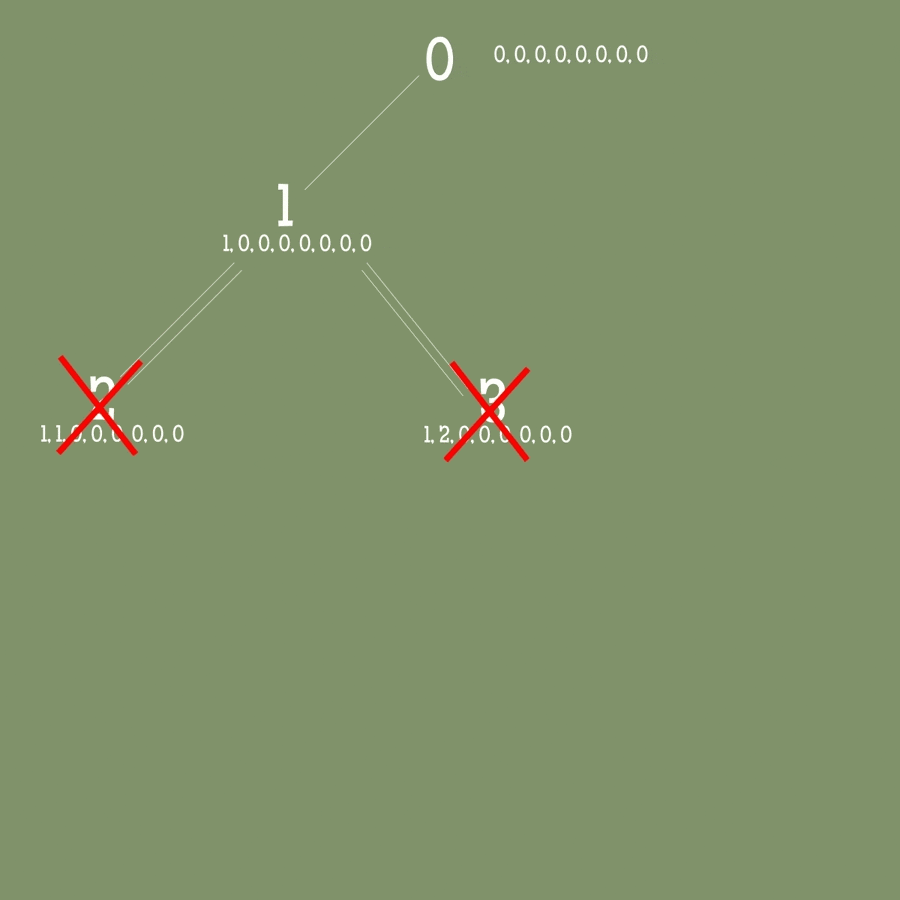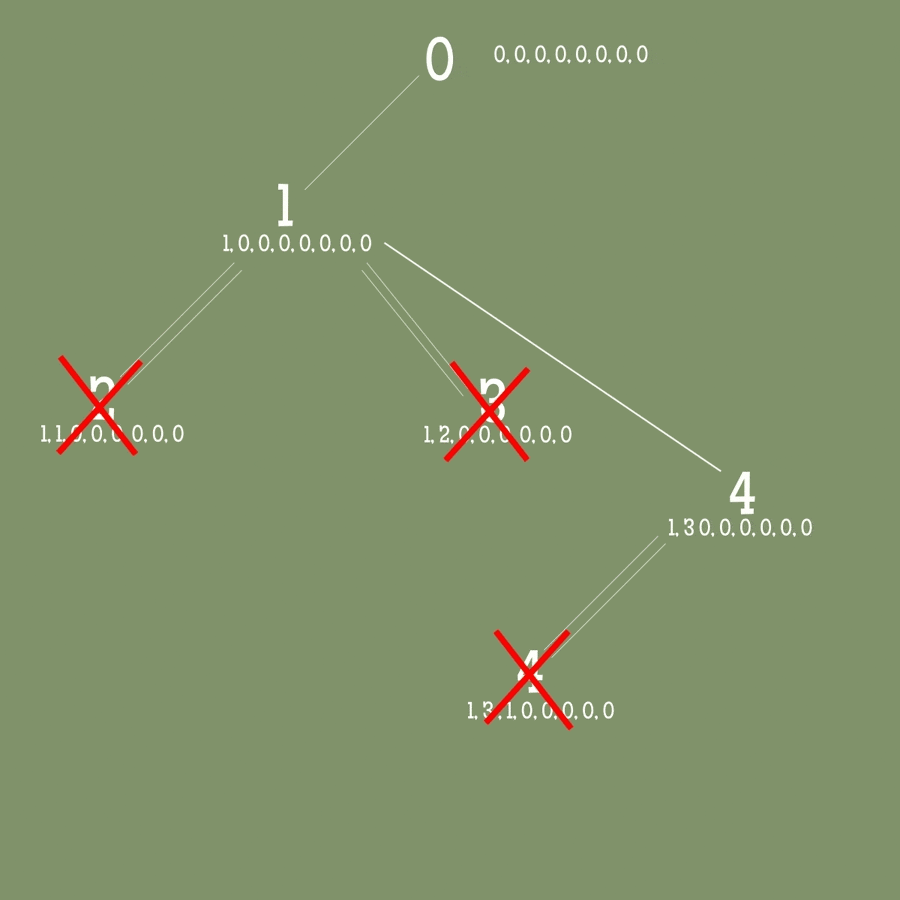エイト・クイーンって?
エイト・クイーンとは、チェスの盤とコマを使用したパズルの名称です。
-
エイト・クイーンのルール: チェスの盤上に、8個のクイーンを配置する。
このとき、どの駒も他の駒に取られるような位置においてはいけない。
さっそく本題
解決方法がいくつ存在するのかを、JavaScriptで実装していきます。
このような問題を解決するにはバックトラッキングを使用します。
バックトラッキングの解法を配列で表現
配列 (N-Queen)
| n0 | n1 | n2 | ...nx |
|---|---|---|---|---|---|---|---|
今回配列で表現したい配置

8Queenなので、8個(0 ~ 7)
| | n0 | n1 | n2 | n3 | n4 | n5 | n6 | n7 |
|---|---|---|---|---|---|---|---|---|---|
| col | 0 | 1 | 2 | 3 | 4 | 5| 6 | 7 |
| row | 2 | 4 | 6 | 8 | 3 | 1 | 7 | 5 |
シンプルに表現すると下記のようになる
| 2 | 4 | 6 | 8 | 3 | 1 | 7 | 5 |
|---|---|---|---|---|---|---|---|---|---|
JavaScriptで表現するとこうなる
const queensPosition = [2, 4, 6, 8, 3, 1, 7, 5];
const queensPosition = [
{ col: 0, row: 2 },
{ col: 1, row: 4 },
{ col: 2, row: 6 },
{ col: 3, row: 8 },
{ col: 4, row: 3 },
{ col: 5, row: 1 },
{ col: 6, row: 7 },
{ col: 7, row: 5 },
];
配列を使ってバックトラッキングを適用
バックトラッキング法は最初の0ノードから始まります。
(0, 0) col: 0, row:0 から順に試していきます。
上記を踏まえて、プログラムを書いてみよう
JavaScript
class QueenPosition {
constructor(rowIndex, columnIndex) {
this.rowIndex = rowIndex;
this.columnIndex = columnIndex;
}
get leftDiagonal() {
return this.rowIndex - this.columnIndex;
}
get rightDiagonal() {
return this.rowIndex + this.columnIndex;
}
}
function isSafe(queensPositions, rowIndex, columnIndex) {
const newQueenPosition = new QueenPosition(rowIndex, columnIndex);
for (let queenIndex = 0; queenIndex < queensPositions.length; queenIndex += 1) {
const currentQueenPosition = queensPositions[queenIndex];
if (currentQueenPosition &&
(newQueenPosition.columnIndex === currentQueenPosition.columnIndex
|| newQueenPosition.rowIndex === currentQueenPosition.rowIndex
|| newQueenPosition.leftDiagonal === currentQueenPosition.leftDiagonal
|| newQueenPosition.rightDiagonal === currentQueenPosition.rightDiagonal)) {
return false;
}
}
return true;
}
function nQueensRecursive(solutions, previousQueensPositions, queensCount, rowIndex) {
const queensPositions = [...previousQueensPositions].map((queenPosition) => {
return !queenPosition ? queenPosition : new QueenPosition(
queenPosition.rowIndex,
queenPosition.columnIndex,
);
});
if (rowIndex === queensCount) {
solutions.push(queensPositions);
return;
}
for (let columnIndex = 0; columnIndex < queensCount; columnIndex += 1) {
if (isSafe(queensPositions, rowIndex, columnIndex)) {
queensPositions[rowIndex] = new QueenPosition(rowIndex, columnIndex);
nQueensRecursive(solutions, queensPositions, queensCount, rowIndex + 1);
queensPositions[rowIndex] = null;
}
}
return;
}
function nQueens(queensCount) {
let queensPositions = [];
let solutions = [];
nQueensRecursive(solutions, queensPositions, queensCount, 0);
console.log('solutions', solutions);
console.log('solutions length', solutions.length);
return;
}
HTML
<button type="button" onClick="nQueens(8)">nQueens</button>