概要
scikit-learnでk-meansを用いてクラスタリングしているときに思いました。
「距離関数をコサイン類似度にしたい」
scikit-learnのk-meansでは距離関数としてユークリッド距離しか使えません。
scikit-learnのコードを書き換えて、独自の距離関数を使えるようにした記事もあります。
しかし、結構面倒くさそうだし処理速度の低下が気になります。
そこでこんな投稿を見つけました。
本投稿はこの投稿を要約・加筆します。
結論を言うと
「正規化してからユークリッド距離をとるとコサイン類似度を測れる」
です。
距離関数の定義
まずユークリッド距離とコサイン類似度の定義を確認しておきます。
2点 $P(x_1, ..., x_n), Q(y_1, ..., y_n)$ に対して、$\vec{x}=(x_1, ..., x_n), \vec{y}=(y_1, ..., y_n)$ とします。
ユークリッド距離は
$$d(P, Q) = |\vec{x} - \vec{y}| = \sqrt{\sum_{k=1}^{n} (x_k-y_k)^2}$$
コサイン類似度は
$$cos(\vec{x}, \vec{y}) = \frac{\vec{x}\cdot\vec{y}}{|\vec{x}||\vec{y}|} = \frac{\sum_{k=1}^{n}x_k y_k}{\sqrt{\sum_{k=1}^{n}x_k^2} \sqrt{\sum_{k=1}^{n}y_k^2} }$$
です。
コサイン類似度をユークリッド距離で測る
$\vec{x}, \vec{y}$ を正規化したものを改めて $\vec{x}, \vec{y}$ とします。
すると、$|\vec{x}| = 1, |\vec{y}| = 1, cos(\vec{x}, \vec{y}) = \vec{x}\cdot\vec{y}$となります。
ここでユークリッド距離を計算すると(ルートを書くのが面倒なので2乗してます。)
\begin{align}
d(P, Q)^2 &= |\vec{x} - \vec{y}|^2 \\
&= |\vec{x}|^2 - 2 \vec{x} \cdot \vec{y} + |\vec{y}|^2 \\
&= 2(1 - cos(\vec{x}, \vec{y}))
\end{align}
つまり、「ユークリッド距離が 0 に近い」と「コサイン類似度が 1 に近い」が同値になります。
また、コサイン類似度はベクトルのなす角によって決まり、正規化はベクトルの長さのみを変更するものなので、正規化前と後でコサイン類似度は変化しません。
よって、
「正規化後のユークリッド距離が近い」⇔「コサイン類似度が高い」
となります。
直感的な理解
2次元で考えるとわかりやすいです。
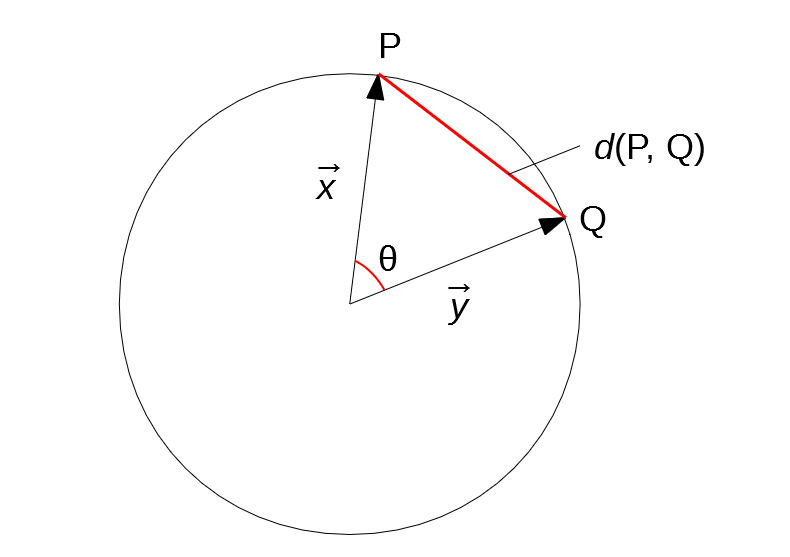
正規化後はP, Qは単位円上にあるので、下図のような状況になります。
$d(P, Q)$ と $\vec{x}, \vec{y}$ のなす角 $\theta$ が連動していることがわかります。
$\vec{x}, \vec{y}$ のコサイン類似度が高いということは、なす角 $\theta$ が小さいということなので、
正規化後では「ユークリッド距離が近い」⇔「コサイン類似度が高い」となります。
コード例
scikit-learnで書く場合は以下のようになります。
from sklearn import preprocessing, cluster
normalized_vec_list = preprocessing.normalize(vec_list)
result = cluster.KMeans(n_clusters=5).fit(normalized_vec_list)
おわり
いちいち距離関数を独自に設定せずとも、ちょっとした工夫(正規化)をするだけでOKというのがお手軽で良いですね。
ただし、コサイン類似度にしか対応できません。
その他の距離関数を使うための工夫があれば是非教えてください。