この記事で紹介すること
- kmeansの距離関数って本当にユークリッド距離大正義なの?
- scikit-learnのk-meansって何が動いているの?
- scikit-learnのk-meansで距離関数を変更するにはどうするの?
k-means法といえば、みなさんご存知、ぐにょぐにょっとデータを分割してくれるアレですね。
教科書にもよく出てくるアレなので、細かい説明は省きますが、いまだに使われてるのは、(禁則事項です)ということですよね。
あ、ちなみにこういう動画とかこういうツールとか使うと、k-meansの動きがよくわかってナイスだと思います。
で、k-meansではセントロイドと各データとの距離を測るために、「距離関数」が必要になります。
教科書的には「ユークリッド距離」一択のことが多いのですが、それって本当に正しいのでしょうか?
この論文, Anna Huang, "Similarity Measures for Text Document Clustering", 2008
はそんな疑問に明快に答えてくれます。
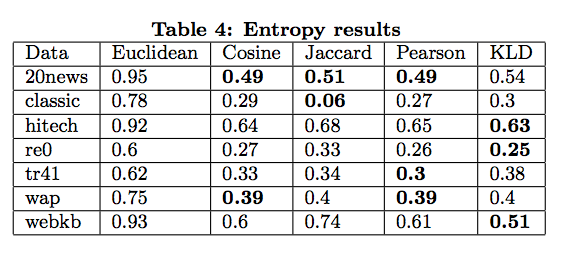
論文から拝借したTable4を見てみましょう。Entropy指標なので、低い方が良いクラスタリングです。
あくまでテキスト分類タスクにおいては、ユークリッド距離が大正義ではないことがわかりますね。
では、他の距離関数も試したくなるのが人情というものです。
scikit-learnでやってみよう
結論からいうと、そーいうオプションはありません。
調べるのメンドクセー。とかじゃなくて、マジでないです。
scikit-learnのコードをみるとそれがわかります。
closest_dist_sq = euclidean_distances(
centers[0, np.newaxis], X, Y_norm_squared=x_squared_norms,
squared=True)
current_pot = closest_dist_sq.sum()
これはk-meansのコード片ですが、ユークリッド距離がハードコードされていることがわかります。
つまり、オプションとして距離関数を変更する余地はないのです。
でも、なんでないのでしょう?githubのissueをみると、「他の距離関数だと、一般化が難しいから」みたいなことが書いてあります。
それでも、隠しオプションにしたらいいと思うんですけどね・・・
じゃあ、どーやって他の距離関数使うのよ!?
いくつか方法はあるみたいです。
- 自分でk-means書く。stack-overflowのページにその方法が書いてあります
- k-centroid法を使う。scikit-learnで利用できるらしいですよ。調べてないけど。
- monkey-patchを利用する。今回はこれをします。
monkey-patchとは、とどのつまり、「メソッドを上書きして好きな処理をする」ことです。
今回は、k-means内のユークリッド距離関数を上書きしてみましょう。このページでその方法が述べられています。
実際に、やってみましょう。
使うデータはここから拝借します。テキストデータではないですが、ご愛嬌ということで・・・
scikit-learnのユークリッド距離の挙動を見てみる
k-meansが呼び出しているユークリッド距離はこれです。
挙動を大きく分けると、
- YがNoneの場合
- Xが1サンプルのarrayでYが複数サンプルのarrayの場合
- Xが2サンプルのarrayでYが複数サンプルのarrayの場合
です。
いずれの場合も、
array([
[XとYの距離]
])
という形のarrayを返却します。
なので、新しく距離関数を定義する時は、このフォーマットに従うことになります。
ピアソン相関係数の距離関数を実装する
論文に紹介されていたピアソンの相関係数を実装してみることにします。pythonではscipyで利用可能です。
ただし、論文でも触れていますが、そのままでは距離関数にはなりません。そこで、ちょっとだけ式変形をします。
special_pearsonr(X, Y) = {
1 - pearsonr(X, Y) if pearsonr(X, Y) > 0,
|pearsonr(X, Y)| else
}
という式変形をします。
では、ユークリッド距離の3つの場合分けを考慮して、実装してみます。
def special_pearsonr(X, Y):
pearsonr_value = scipy.stats.pearsonr(X, Y)
if pearsonr_value[0] < 0:
return abs(pearsonr_value[0])
else:
return 1 - pearsonr_value[0]
def sub_pearsonr(X, row_index_1, row_index_2):
pearsonr_distance = special_pearsonr(X[row_index_1], X[row_index_2])
return (row_index_1, row_index_2, pearsonr_distance)
def pearsonr_distances(X, Y=None):
if Y==None:
# Xだけが入力されていて、Xが2d-arrayの場合
row_combinations = list(combinations(range(0, len(X)), 2))
pearsonr_set = [sub_pearsonr(X, index_set_tuple[0], index_set_tuple[1]) for index_set_tuple in row_combinations]
matrix_source_data = pearsonr_set + map(copy_inverse_index, pearsonr_set)
row = [t[0] for t in matrix_source_data]
col = [t[1] for t in matrix_source_data]
data = [t[2] for t in matrix_source_data]
pearsonr_matrix = special_pearsonr((data, (row, col)), (X.shape[0], X.shape[0]))
return pearsonr_matrix.toarray()
elif len(X.shape)==1 and len(Y.shape)==2:
# Xが1サンプルでYが複数サンプルの場合
# returnは1 sampleのarray
pearsonr_set = numpy.array([special_pearsonr(X, Y[y_sample_index]) for y_sample_index in range(0, Y.shape[0])])
return pearsonr_set
elif len(X.shape)==2 and len(Y.shape)==2:
# 1行には、X[i]とY[j] in n(Y)の距離を記録して返す
# X[i]とYのすべての距離を計算する関数
pearsonr_x_and_all_y = lambda X, Y: numpy.array([special_pearsonr(X, Y[y_sample_index]) for y_sample_index in range(0, Y.shape[0])])
pearsonr_divergence_set = numpy.array([pearsonr_x_and_all_y(X[x_i], Y) for x_i in range(0, X.shape[0])])
return pearsonr_divergence_set
else:
raise Exception("Exception case caused")
pearsonr_distancesがk-meansで呼び出す距離関数です。
で、次にユークリッド距離関数をmonkey-patchしてみましょう。
start = time.time()
# 入力を保証するため、ユークリッド距離関数と同じパラメタを持つ関数を用意する
def new_euclidean_distances(X, Y=None, Y_norm_squared=None, squared=False):
return pearsonr_distances(X, Y)
from sklearn.cluster import k_means_
# ここで上書き!
k_means_.euclidean_distances = new_euclidean_distances
kmeans_model = KMeans(n_clusters=3, random_state=10, init='random').fit(features)
print(kmeans_model.labels_)
elapsed_time = time.time() - start
print ("Pearsonr k-means:{0}".format(elapsed_time))
実行時間を見たかったので、ついでに時間も計測することにします。
言い忘れていましたが、データは
features = numpy.array([
[ 80, 85, 100 ],
[ 96, 100, 100 ],
[ 54, 83, 98 ],
[ 80, 98, 98 ],
[ 90, 92, 91 ],
[ 84, 78, 82 ],
[ 79, 100, 96 ],
[ 88, 92, 92 ],
[ 98, 73, 72 ],
[ 75, 84, 85 ],
[ 92, 100, 96 ],
[ 96, 92, 90 ],
[ 99, 76, 91 ],
[ 75, 82, 88 ],
[ 90, 94, 94 ],
[ 54, 84, 87 ],
[ 92, 89, 62 ],
[ 88, 94, 97 ],
[ 42, 99, 80 ],
[ 70, 98, 70 ],
[ 94, 78, 83 ],
[ 52, 73, 87 ],
[ 94, 88, 72 ],
[ 70, 73, 80 ],
[ 95, 84, 90 ],
[ 95, 88, 84 ],
[ 75, 97, 89 ],
[ 49, 81, 86 ],
[ 83, 72, 80 ],
[ 75, 73, 88 ],
[ 79, 82, 76 ],
[ 100, 77, 89 ],
[ 88, 63, 79 ],
[ 100, 50, 86 ],
[ 55, 96, 84 ],
[ 92, 74, 77 ],
[ 97, 50, 73 ],
])
です。実行してみると、
[0 0 0 1 1 2 1 0 2 1 0 2 2 0 0 1 1 0 1 0 2 0 2 0 2 2 1 1 2 1 1 2 2 2 1 2 2]
Pearsonr k-means:11.0138161182
としっかり動いていることが確認できました!ヤッタネ!
ちなみに、通常のk-means、ユークリッド距離バージョンは
[1 1 0 1 1 2 1 1 2 1 1 1 2 1 1 0 2 1 0 0 2 0 2 0 1 1 1 0 2 2 2 2 2 2 0 2 2]
========================================
Normal k-means:0.016499042511
です。0と1のクラスターが違うデータがいつくか確認できますね。
実行時間は・・・残念ながら、600倍近くの差がでてしまいました・・・
呼び出す関数が増えてしまったので、仕方がありません。このあたり、実装を工夫すれば、もう少し早くなる可能性は十分にありそうです。(早くしてくれるエロい人。募集)
特に文書分類に使っていないので、差分は見てませんが、論文で実証はされているので、ピアソンの相関係数はきっと良い結果を出してくれる(はず・・)
まとめ
- k-meansの距離関数はユークリッド距離の大正義ではない
- scikit-learnで他の距離関数使うのは少し骨が折れる
- 遅い
ちなみに・・・
カルバック・ライブナー距離も実装してみました。ただ、残念ながら、エラーが出て止まります。
X, Yの距離を計測すると、どうしてもマイナス要素が発生してしまい、距離がinfになってしまうため、そもそも初期化すらできません。
マイナス要素をどうにかすればいいんでしょうけど、どうしたらいいんだろう。特に論文でも触れていませんでした。
from sklearn.preprocessing import normalize
def averaged_kullback_leibler(X, Y):
#norm_X = normalize(X=X, norm='l1')[0]
#norm_Y = normalize(X=Y, norm='l1')[0]
norm_X = X
norm_Y = Y
pie_1 = norm_X / (norm_X + norm_Y)
pie_2 = norm_Y / (norm_X + norm_Y)
M = (pie_1 * norm_X) + (pie_2 * norm_Y)
KLD_averaged = (pie_1 * scipy.stats.entropy(pk=norm_X, qk=M)) + (pie_2 * scipy.stats.entropy(pk=norm_Y, qk=M))
return KLD_averaged
def sub_KL_divergence(X, row_index_1, row_index_2):
#kl_distance = scipy.stats.entropy(pk=X[row_index_1], qk=X[row_index_2])
kl_distance = averaged_kullback_leibler(X[row_index_1], X[row_index_2])
return (row_index_1, row_index_2, kl_distance)
def copy_inverse_index(row_col_data_tuple):
return (row_col_data_tuple[1], row_col_data_tuple[0], row_col_data_tuple[2])
def KLD_distances(X, Y=None):
if Y==None:
# Xだけが入力されていて、Xが2d-arrayの場合
row_combinations = list(combinations(range(0, len(X)), 2))
kl_divergence_set = [sub_KL_divergence(X, index_set_tuple[0], index_set_tuple[1]) for index_set_tuple in row_combinations]
matrix_source_data = kl_divergence_set + map(copy_inverse_index, kl_divergence_set)
row = [t[0] for t in matrix_source_data]
col = [t[1] for t in matrix_source_data]
data = [t[2] for t in matrix_source_data]
kl_distance_matrix = scipy.sparse.csr_matrix((data, (row, col)), (X.shape[0], X.shape[0]))
return kl_distance_matrix.toarray()
elif len(X.shape)==1 and len(Y.shape)==2:
# Xが1サンプルでYが複数サンプルの場合
# returnは1 sampleのarray
kl_divergence_set = numpy.array([averaged_kullback_leibler(X, Y[y_sample_index]) for y_sample_index in range(0, Y.shape[0])])
return kl_divergence_set
elif len(X.shape)==2 and len(Y.shape)==2:
# 1行には、X[i]とY[j] in n(Y)の距離を記録して返す
# X[i]とYのすべての距離を計算する関数
for x_i in range(0, X.shape[0]):
xx = X[x_i]
for y_sample_index in range(0, Y.shape[0]):
#print(xx)
#print(Y[y_sample_index])
print(averaged_kullback_leibler(xx, Y[y_sample_index]))
kld_x_and_all_y = lambda X, Y: numpy.array([averaged_kullback_leibler(X, Y[y_sample_index]) for y_sample_index in range(0, Y.shape[0])])
kl_divergence_set = numpy.array([kld_x_and_all_y(X[x_i], Y) for x_i in range(0, X.shape[0])])
return kl_divergence_set
else:
raise Exception("Exception case caused")