はじめに
計算機のハードウェアの進歩により、最近では3D表現を用いたゲームやプログラムは手軽なものになりました。例えばJavaScriptではThree.jsのようなライブラリを用いることで手軽に3D表現を用いた作品を作ることができます。
今回は上記のようなリッチなライブラリには目もくれず、原始的な3D表現をJavaScriptで実装しようと思います。趣旨としては、簡易的な3D表現の単純さ、JavaScriptエンジンのパフォーマンスの体感、あたりになります。JavaScriptの実行エンジンはとても高度に最適化されており、C言語と同等までには届きませんが、スクリプト言語としてはとても高速に動作することが特徴です。
真面目に向き合わなければならない課題はきちんとこなしつつ、JavaScriptの高速さの影に隠れて楽をできるところは楽してしまおう、という感じで進めていきたいと思います。
作るもの
今回作成するものは、プログラムで作成するものに関しては、
- 3D座標から2D座標への変換
- 2D座標から3D座標への変換
の2つがメインで、 - 固定カメラでの処理
- カメラが動く場合の処理
のバリエーションに展開して行きます。
絵として描画されるものは次のような、立方体が回転しているように見えるというシンプルなものです。

座標を扱うオブジェクト
ここは各々好みがあると思いますが、
/* 2D座標 */
let a = {
x : -0.5,
y : -0.5
}
/* 3D座標 */
let b = {
x : -0.5,
y : -0.5,
z : -0.5
}
のように扱うものとして進めます。
描画する領域を準備し、四角形を描画する関数を作る
今回はHTML要素のcanvasタグに描画したいと思います。canvasタグは描画エリアの左上が(0,0)です。今回扱うプログラムでは、描画エリアの中央が(0,0)の方が都合が良いので、図形を描画する関数を少し工夫して作ります。例えば次のようにします。
/* 四角形を描画する(2次元座標) */
function quadrangle_2d(selector, fillstyle, p1, p2, p3, p4){
let canvas = $(selector);
let width_px = $(canvas).width();
let height_px = $(canvas).height();
let scale_px = width_px;
if (scale_px > height_px){
scale_px = height_px;
}
scale_px /= 2.0;
let o_px_x = width_px / 2.0;
let o_px_y = height_px / 2.0;
let o = $(canvas).get(0);
let c = o.getContext("2d");
c.beginPath();
c.moveTo(p1.x * scale_px + o_px_x, p1.y * scale_px + o_px_y);
c.lineTo(p2.x * scale_px + o_px_x, p2.y * scale_px + o_px_y);
c.lineTo(p3.x * scale_px + o_px_x, p3.y * scale_px + o_px_y);
c.lineTo(p4.x * scale_px + o_px_x, p4.y * scale_px + o_px_y);
c.closePath();
c.fillStyle = fillstyle;
c.fill();
}
上記のコードでは、(0,0)を描画する中央に持ってきただけではなく、canvasタグのピクセル数も抽象化して、描画エリアが正方形のとき、カドが(-1,-1)から(1,1)になるように変換しています。こうすることで、canvasタグの実際のピクセル数を気にすることなく話を進めることができます。
※ピクセル数が偶数、奇数のときで端が1pxズレるとか、そういう突っ込みはしないでください。
※「getContext("2d")」で気付いた方もいらっしゃると思いますが、WebGLという便利なヤツもいます。本記事の趣旨と外れるので興味のある方は他所のコンテンツをご参照ください。
次のコードで実際の描画を確認します。
let a = {
x : -0.5,
y : -0.5
}
let b = {
x : 0.5,
y : -0.5
}
let c = {
x : 0.5,
y : 0.5
}
let d = {
x : -0.5,
y : 0.5
}
quadrangle_2d('#canvas', '#0FF', a, b, c, d)
3D座標を2D座標に変換する(固定カメラ)
3Dで扱う座標は3次元ですが、表示するディスプレイは2次元です。ですので、3Dの座標を2Dの座標に変換(投影)する必要があります。今回は、ディスプレイの横をx、縦をy、奥行きをzとして扱うことにします。(x,y,z)の値を(x',y')に投影します。
処理の内容を簡略化するために、カメラは(x,y,z)=(0,0,cam_z)にあり、常に原点を向いていることにします。
※カメラを上記の軸上で回転させることもできるじゃないか、という突っ込みは勘弁してください。
処理は単純で、(カメラのz座標と変換したい3D座標のz座標との距離)と、(カメラのz座標と原点との距離)との比率で拡大率を決めて、遠いほどx, yを小さくするという方法です。コードとしては次のとおりです。
// cam_zがカメラまでの距離、カメラは(x,y,z)=(0,0,cam_z)にあり、常に原点を向いていることにする
function quadrangle_3d(selector, fillstyle, p1, p2, p3, p4){
p_2d_1 = {
x : p1.x * cam_z / (cam_z + p1.z),
y : p1.y * cam_z / (cam_z + p1.z)
};
p_2d_2 = {
x : p2.x * cam_z / (cam_z + p2.z),
y : p2.y * cam_z / (cam_z + p2.z)
};
p_2d_3 = {
x : p3.x * cam_z / (cam_z + p3.z),
y : p3.y * cam_z / (cam_z + p3.z)
};
p_2d_4 = {
x : p4.x * cam_z / (cam_z + p4.z),
y : p4.y * cam_z / (cam_z + p4.z)
};
quadrangle_2d(selector, fillstyle, p_2d_1, p_2d_2, p_2d_3, p_2d_4);
}
試しに、塗りつぶしなしで立方体を描画してみます。
3Dっぽく描画できています。
見えない面を隠す
丁寧に実装された3Dエンジンでは、面は表と裏があり、画面上に表示するかどうかの条件を満たした場合のみ描画されます。隠面処理と呼ばれます。汎用的な3Dエンジンが手に入らなかった時代にゲームなどを実装していた経験のあるエンジニアなら、大抵は嫌な思い出なのではないでしょうか。隠面処理は高性能な3Dエンジンを作る上では欠かせない処理ですが、現代のJavascriptが高速であるが故に横着することができます。今回はシンプルに、画面から遠い順に描画する、という処理にしてみました。仕組みは単純で、見えなくなる面は見えてる面で上書きしてしまえば、表示上は辻褄が合うはずです。
/* 立方体を描画する */
/* カメラから近い順に3面描画すれば辻褄が合う */
function render_cube(selector, cube) {
cube.face.sort(function (a, b){
let av_a = {
x : (a.p1.x + a.p2.x + a.p3.x + a.p4.x) / 4,
y : (a.p1.y + a.p2.y + a.p3.y + a.p4.y) / 4,
z : (a.p1.z + a.p2.z + a.p3.z + a.p4.z) / 4,
};
let av_b = {
x : (b.p1.x + b.p2.x + b.p3.x + b.p4.x) / 4,
y : (b.p1.y + b.p2.y + b.p3.y + b.p4.y) / 4,
z : (b.p1.z + b.p2.z + b.p3.z + b.p4.z) / 4,
};
let cam = {
x:0,
y:0,
z:cam_z
}
let da = Math.sqrt((cam.x - av_a.x) * (cam.x - av_a.x) + (cam.y - av_a.y) * (cam.y - av_a.y) + (cam.z - av_a.z) * (cam.z - av_a.z));
let db = Math.sqrt((cam.x - av_b.x) * (cam.x - av_b.x) + (cam.y - av_b.y) * (cam.y - av_b.y) + (cam.z - av_b.z) * (cam.z - av_b.z));
return da - db;
});
for (let i = 3 ; i < 6 ; i++){
e = cube.face[i];
quadrangle_3d(selector, e.color, e.p1, e.p2, e.p3, e.p4);
}
}
処理の雰囲気は上記のようになります。この方法では、表示する立体が凸多面体である場合にうまく動作します。この関数で立方体の描画を行い、ついでに回転させると、

このように3Dっぽく描画できていることがわかります。
カメラが動く場合の3D座標から2D座標への変換(射影)
線形代数の諸々のテクニックを用いれば見た目だけはカメラが動いているように見せかけることは可能です。しかし、実際にアプリケーションを実装するときは、表示するオブジェクトの座標とカメラの座標は別々に管理して、オブジェクトが動いたのかカメラが動いたのかを区別できた方が便利です。カメラ位置を固定したことにより簡略化されていた処理を、カメラが動く場合を想定して書き直します。
線形代数の基礎的な知識があれば、内積、ベクトル積、の操作で高次元の値を目的の次元数へ次元を落とす(射影する)方法がわかると思います。ベクトルを操作する関数をいくつか用意します。
/* 符号反転 */
function neg(p){
return {
x: - p.x,
y: - p.y,
z: - p.z
};
}
/* ベクトル ÷ スカラー */
function vec_div(a, div){
return {
x:a.x / div,
y:a.y / div,
z:a.z / div
};
}
/* ベクトル × スカラー */
function vec_mul(a, mul){
return {
x:a.x * mul,
y:a.y * mul,
z:a.z * mul
};
}
/* ベクトル + ベクトル */
function vec_add(a, b){
return {
x:a.x + b.x,
y:a.y + b.y,
z:a.z + b.z
};
}
/* ベクトル - ベクトル */
function vec_sub(a, b){
return {
x:a.x - b.x,
y:a.y - b.y,
z:a.z - b.z
};
}
/* ノルム */
function norm(p){
return Math.sqrt(p.x * p.x + p.y * p.y + p.z * p.z);
}
/* 内積 */
function d_product(a, b){
return a.x * b.x + a.y * b.y + a.z * b.z;
}
/* ベクトル積 */
function v_product(a, b){
return {
x:a.y * b.z - a.z * b.y,
y:a.z * b.x - a.x * b.z,
z:a.x * b.y - a.y * b.x
};
}
これらの操作を用いることで、3Dから2Dへ射影する操作は、
function R3toR2(cam, p){
let nx, ny, nz;
let ret = {
x: 0,
y: 0
};
nx = cam.n;
ny = v_product(neg(cam.pos), nx);
ny = vec_div(ny, norm(ny));
nz = vec_div(cam.pos, norm(cam.pos));
pn = vec_sub(p, cam.pos);
let ratio = norm(cam.pos) / d_product(pn, neg(nz));
pn = vec_mul(pn, ratio);
ret.x = d_product(nx, pn);
ret.y = d_product(ny, pn);
return ret;
}
上記のように書くことができます。このとき、カメラ位置はcam.pos、原点方向を向いており、カメラの軸の向きをcam.nで表しています。ベクトルへの演算それぞれをベタ書きしてしまうと結構なコード量になりますが、内積、ベクトル積で簡単に記述できることがわかります。
立方体本体を回転させた例と同じ回転軸、回転量をカメラに対して与えたので、見た目上の回転方向は逆になっています。意図した通りの動作が実現できました。
ここからが本番
3Dの表現で視点を切り替えたとき、オブジェクト自体を動かす場合は、そのオブジェクトの論理的な位置がどこなのか管理が難しくなります。カメラを動かす場合は、映っている画面そのものの位置を管理するのが難しくなります。どちらをとっても、同じ原理で大変な作業が待っています。具体的には、カメラの移動に伴いマウスポインタの座標は3次元で扱わなければならない点、マウスポインタと画面上の面が重なり合っている場合の、面の上の論理座標を求めるのが難しい、の2点です。
ちょっと長く書いてしまいましたが、平たく言えば、3Dから2Dへの変換は次元を落とすだけで簡単なのですが、2Dから3Dへ戻すのがかなり面倒ということです。
絵にしてみると、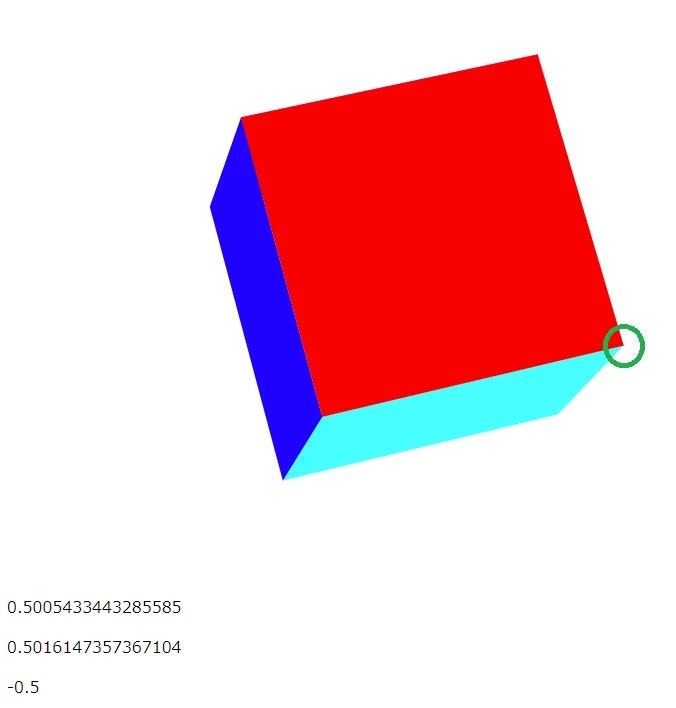
画像の赤の面の右下(緑〇)の座標は(0.5, 0.5, -0.5)で設定されています。マウスカーソルを緑〇のところへ重ねて、マウス座標を赤の面の座標に射影したときの座標を表示しています。マウスカーソルが緑の〇で囲まれたカドにあることがわかります(スクリーンショットにマウスカーソルが映っていませんが、〇の中にカーソルがあります)。
このように、カメラがまっすぐではないときにマウスがオブジェクトに接触した、という状況で、マウスがオブジェクト上のどこに接触しているのか、を算出するのが意外と面倒なのです。
何かゲームを作りたい、といったときに、マウスで画面内のオブジェクトをドラッグしたい、という要望を叶えるのが難しくて諦めてしまった人は多いと思います。
この処理は、3D->2Dへの変換と対になる逆変換を作らなければなりません。この逆変換を一発で作ろうと思うと大変なのですが、2D上のマウスポインタの座標を、カメラのスクリーン上の3Dの座標へ変換、スクリーン上の3D座標を任意の平面に射影の2つの段階を踏むことで、けっこう簡単に実現できます。
マウスポインタをカメラのスクリーン座標に変換
今回、カメラが動くので、ディスプレイ上で見えている値はカメラのスクリーン上の相対座標です。マウスの絶対座標を得ると、その値は即ちスクリーン上の相対座標です。この値を、カメラのスクリーンが実際にどの位置にあるのか、を考慮して論理的な絶対座標に戻します。
数学的な細かいことは線形代数の参考書を読んでいただければと思います。カメラに由来する基底とマウス座標の積をコネコネすることで欲しい値になります。
let mousePos = getMousePos('#canvas', e);
mousePos3d = mousePosTo3d(cam, mousePos);
/* マウスの座標((-1, -1)~(1, 1))を得る */
function getMousePos(selector, e){
let canvas = $(selector);
mx = e.pageX - canvas.position().left;
my = e.pageY - canvas.position().top;
let width_px = $(canvas).width();
let height_px = $(canvas).height();
let scale_px = width_px;
if (scale_px > height_px){
scale_px = height_px;
}
scale_px /= 2.0;
let o_px_x = width_px / 2.0;
let o_px_y = height_px / 2.0;
let x = (mx - o_px_x) / scale_px;
let y = (my - o_px_y) / scale_px;
return {x:x, y:y};
}
/* スクリーン上の絶対座標にする */
function mousePosTo3d(cam, pos){
let nx = cam.n;
let ny = v_product(neg(cam.pos), nx);
ny = vec_div(ny, norm(ny));
return vec_add(vec_mul(nx, pos.x), vec_mul(ny, pos.y));
}
この関数の戻り値は直感的にはよくわからない値が返ってくるのですが、この値を適当なオブジェクトの面に射影するコードを作り、その結果を見ると、
function mousePosToFacePos(cam, face, p){
let fv1 = vec_sub(face.p1, face.p2);
let fv2 = vec_sub(face.p3, face.p2);
let fn = v_product(fv1, fv2);
fn = vec_div(fn, norm(fn));
fd = - d_product(face.p1, fn);
let q = cam.pos;
let v = vec_sub(p, q);
let t = - (d_product(fn, q) + fd) / d_product(fn, v);
let r = vec_add(q, vec_mul(v, t));
return r;
}
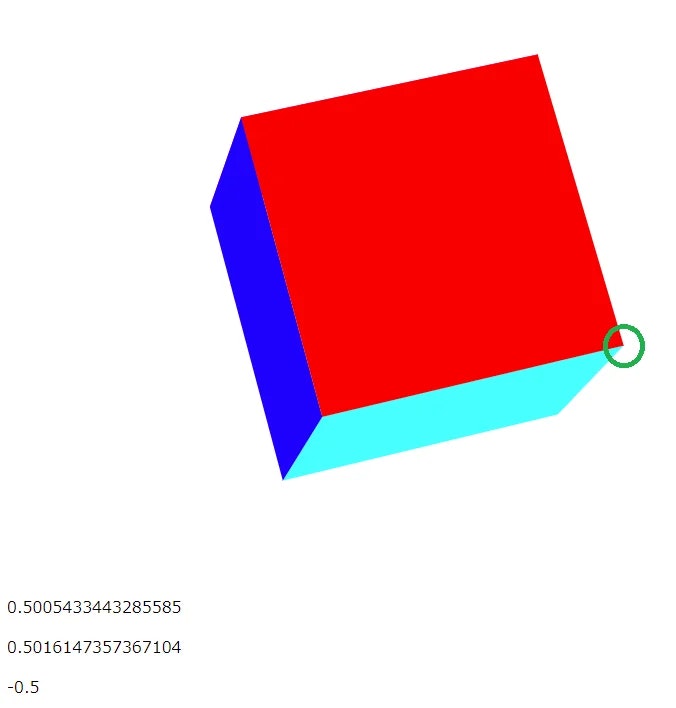
このように、オブジェクト上の座標に戻すことができます。
ただし、これでも大変なところは隠してあります。カメラは原点を向いている前提です。 これがカメラが様々な方向を向く、となると、やはり大変になってしまうのです。
本記事では、ここまでで一旦筆を置きたいと思います。なぜなら、作りたいものが有名な立方体パズル、ルービックキューブゲームだからです。ここに書いた内容で必要な道具は揃いました。次回の記事でお会いしましょう

