はじめに
株式会社エイチームコマーステックの@o93です.
近頃はデータ分析基盤構築のお仕事が中心で,直近は事業評価の仕組み化に取り組んでいます.事業を作るフェーズにおいて,得られるデータは多くありません.ただ統計値をそのまま表示するだけでなく,評価指標がどれくらい信頼できるのか,その不確かさを定量的に示すことができれば,より正しい意思決定が行えそうです.
そこで今回は,誤差/曖昧さ/不確かさの基礎と誤差を手軽に求める方法について色々と調べてみました.本記事についても難しい数式や理論的な説明は省略していますので,詳しい数式や説明はそれぞれのリンクを参照ください,,,
手軽さ
手軽さの定義は人によって大きく異なるかと思いますが,ローカルではなくブラウザ上で実行できれば良しとしました.具体的には,
- 言語
- ツール
- ライブラリ
これらを使用します.この記事に掲載されているコードは以下のColabで実行できます.
Pythonはハードル高い..という方向けにGoogle SheetsやBigQueryでの一部実装を行いました,,,一部計算方法をおまけに記載していますので,参照ください!
誤差(Error)とは?
事象を測定したり計算して得られた値と,理論的に正しい真の値との差を誤差と言います.詳細は以下参照.
誤差には様々な原因がありますが,今回の記事で扱うのはあくまで誤差の見える化です.誤差の原因を特定して補正する内容については詳しく記載しません,,,
誤差の影響を最小限にするため,事象に近い場所で測定値を得たり,値のズレやノイズを取り除くなどの工夫は必要です.それらの工夫を出来るだけ正確に行うために,誤差の算出が役立つはずです.また工夫を施しても誤差がゼロになることは稀で,特に事象から得られるデータが少ない場合,誤差が無視できない程大きくなります.そのようなケースでは,値の誤差を曖昧さ/不確かさとして推定し,意思決定に役立てることができると考えます.
また,理論値や真の値が1つの値に収束するとは限らない点にも注意が必要です.例えばとあるサービスの継続月数について,その平均値(期待値)は1つの値として算出できますが,どんなに精度良く測定したとしても,ユーザーの状況は人それぞれで,1点に収束しません.つまり誤差が0にならずに,ばらついて分布している状態が真の値,ということもありえます.
既知(Known)
まずは真の値が分かっている場合の誤差の算出についてです.
正解の値が既に分かってるなら誤差を出す必要無いじゃないか,と思うかもしれませんが,誤差の原因の特定や,正解値と予測値の誤差を最小化する機械学習モデルの学習に活用されています.
差(Difference)
得られた値から真の値の差を求めれば,最もシンプルな誤差の値になります.
まずは使用するライブラリのインポートから.
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
%precision 3
np.set_printoptions(precision=3)
1つの真の値に対して差を求めてみます.
target_value = 5
sample_value = 3.6
target_value - sample_value
1.4
ただの引き算ですが,ちゃんとした誤差です,,,
値が複数の場合も,それぞれの差を同様に求めることができます.
target_values = np.array([1, 2, 3, 4, 5])
sample_values = np.array([0.9, 1.7, 3.12, 3.87, 5.02])
target_values - sample_values
array([ 0.1 , 0.3 , -0.12, 0.13, -0.02])
複数の差として,正や負の値が並んでいます.ここで,正解データに対する誤差の平均を求めたくなりますが,正負が混ざっているため,値の平均を取ると誤差が相殺されてしまいます,,,
平均絶対誤差(Mean absolute error/MAE)
そこで,誤差の絶対値を計算した上で平均値を求めるのが,MAEです.誤差を上手く平均化できていますね!
float(np.mean(np.abs(target_values - sample_values)))
0.134
準備のところで3桁表示の設定を書いているのに丸め誤差が表示されて見辛いためfloatを使用していますが,本来は不要です.
scikit-learnの関数を使用することで,より簡単に求めることができます.
from sklearn.metrics import mean_absolute_error
float(mean_absolute_error(target_values, sample_values))
0.134
平均二乗誤差(Mean squared error/MSE)
MAEは差の絶対値の平均ですが,MSEは2乗の平均です.実行結果は同じなので,scikit-learn版も併記します.
float(np.mean(np.square(target_values - sample_values)))
from sklearn.metrics import mean_squared_error
float(mean_squared_error(target_values, sample_values))
0.026
値がMAEより小さくなってしまっています,,,これはMSEが差を2乗しているためです.従ってMSEは,誤差の規模感を正しく把握することが難しい指標であると言えます.もちろんMSE同士を比較する分には問題ありません.
二乗平均平方根誤差(Root mean squared error/RMSE)
MSEの平方根を計算することで,↑の問題を解決しているのがRMSEです.
float(np.sqrt(np.mean(np.square(target_values - sample_values))))
float(np.sqrt(mean_squared_error(target_values, sample_values)))
0.162
MAEより値が少し大きいですね..これはRMSEが2乗を平均してから最後に平方根しているためです.RMSEは元のデータと同じ規模感にはなりますが,外れ値がより大きい誤差として扱われる特徴があるようです.
ちなみに,まったく同じ値を入力した場合すべての誤差が0.0になります.例えば機械学習の学習フェーズでは,誤差が出来るだけ小さくなるように,パラメータ調整・予測・評価を繰り返してモデルを改善していきます.
正解率(Binary accuracy)
これまで挙げてきた誤差は値が整数/実数である場合に活用できますが,正解率は値が0と1の2種類しかない場合に使用します.言葉のまま正解数をデータの数で割った数値になります.
target_values = np.array([0, 0, 1, 1, 0, 1])
sample_values = np.array([0, 0, 1, 1, 1, 1])
float((target_values == sample_values).sum() / target_values.shape[0])
from sklearn.metrics import accuracy_score
float(accuracy_score(target_values, sample_values))
0.833
正解率はすべて正解で1.0,すべて不正解で0.0になるため,誤差ではありません.他の誤差と同じようにすべて正解の場合を0.0としたいときは,正解率を1.0から減算すればOKです.
今回挙げた誤差はほんの一部です.例えば分類問題に使用される誤差(以下参照)など,用途に応じて様々なものがあります.もちろん誤差の活用は機械学習だけではありません.理論値と測定値の誤差や,手動で予測したデータと正解データの誤差は,測定器や予測ロジックの比較や改善に役立てることができます!
未知(Unknown)
真の値が分かっていない場合は,最初に真の値を推定してから推定値と値との誤差を更に推定することになります.既知の場合と違って正解が存在しないため,1つの値だけで誤差を算出することはできません,,,真の値が未知である場合の誤差を算出するには,1つの推定値や誤差を算出するために,複数の値が必要になることに注意してください.
偏差(Deviation)
1つの値と基準値との差のことを偏差と言います.基準値として今回は,平均(Mean) を用いることにします.平均はあくまで,得られたデータから真の値を推定するための統計値の1つです.
sample_values = np.array([3.948, 4.42, 3.81, 4.219, 4.03, 4.1, 3.97, 4.35, 3.7, 3.9])
m = sample_values.mean()
print(m)
print(sample_values - m)
4.0447
array([-0.097, 0.375, -0.235, 0.174, -0.015, 0.055, -0.075, 0.305,
-0.345, -0.145])
平均値である4.0447との誤差をそれぞれ求めることができています.既知の場合と同じように誤差の平均を求めたくなりますね,,,
標準偏差(Standard deviation)
連続値(Continuous value)
偏差を2乗した平均の平方根です.基準値に平均を用いていること以外は既知のRMSEと同じで,2乗によって大きくなった数値を平方根によって元の規模感に戻しています.numpy.std()だけで算出できます.
float(sample_values.std())
0.219
標準偏差の詳細については,以下を参照ください.
値$\mu$の分布が正規分布に従うと仮定した場合,値が標準偏差$\pm\sigma$の範囲に収まる確率は以下のようになります.
| 範囲 | 確率 |
|---|---|
| $\pm\sigma$ | 約68.27% |
| $\pm2\sigma$ | 約95.45% |
| $\pm3\sigma$ | 約99.73% |
これを覚えておけば,標準偏差を求めるだけで値がどのくらいばらつくのか,定量的に示すことができます!これを68-95-99.7則と言うようです.
2値(Binary)
コインの表と裏など,2つの値しか取らない場合は分布が正規分布になりません.その平均値は1が出る確率を表します.とりうる値が0と1しかないため誤差をイメージし辛いのですが,平均値(1が出る確率)の誤差を定量的に出すことができれば,意思決定に使えそうです!
一例として,Webサイトの訪問者が一定の確率で商品を購入した場合を1,購入しなかった場合を0と表したデータを擬似的に作成します.
np.random.seed(0)
data = (np.random.rand(100) <= 0.04).astype(np.uint8)
data
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0], dtype=uint8)
訪問者113人のうち,一定の確率で商品が購入されるデータを疑似的に作りました.たまたま5件購入されることになりましたが,これはあくまで偶然そうなった,という想定です,,,いったんそのまま平均値と標準偏差を求めてみることにします.
float(data.mean()), float(data.std())
(0.044, 0.206)
平均値(購入率)が0.044になったことには納得できますが,ばらつきである標準偏差が0.206になってしまっています,,,値が0と1しかないため,この標準偏差が平均値の誤差を上手く推定できていると言えません.ここでライブラリを使えば,確率分布を推定して誤差を算出することは可能なのですが,確率の知識とライブラリのインストールが必要で手軽さに欠けるため,偶然を演出する方法でより簡易的に誤差の算出を試みました.
以下によるとリサンプリング(Resampling) というようです.
upsampling_data = np.tile(data, 100)
means = []
for _ in range(1000):
m = np.random.choice(upsampling_data, data.shape[0]).mean()
means.append(m)
float(data.mean()), float(np.std(means))
(0.044, 0.019)
以下のような流れで標準偏差を算出しています.
-
np.tileでデータをアップサンプリング - アップサンプリングしたデータの中から元のデータ数分だけサンプリング
- サンプリングしたデータから平均値を計算
- 2〜3を
1000回繰り返す - 1000個の平均値から標準偏差を算出
4.4±1.9%つまり,2.5〜6.3%と計算できました.113件中の購入が5件である場合の誤差なので,それっぽい値,,,分布を表示してみます.
plt.figure(figsize=(10, 6))
sns.histplot(means, bins=12, stat='probability')
plt.show()
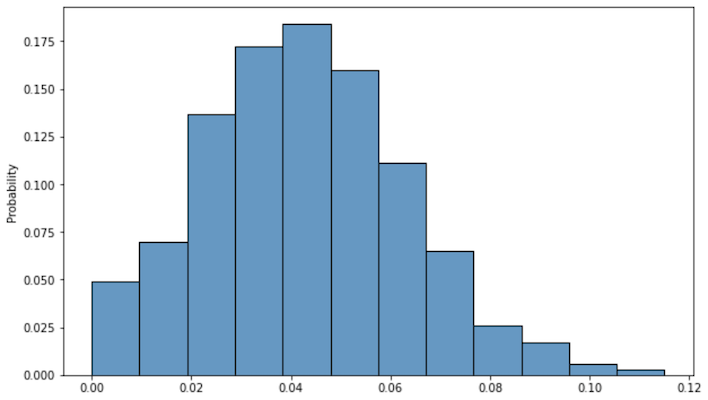
それっぽい分布,,,標準偏差(誤差の平均)の範囲も問題無さそうです.分布の形が左右対象でないのは,購入率が負になることは無いためと思われます.もちろんデータが増えれば分布の幅は狭くなっていきます.
おわりに
今回は,誤差を手軽に算出する方法について紹介しました.とても基礎的な内容でコードもシンプルですが,実際にデータ分析や機械学習で使用している内容も含んでいます.個人的には,施策効果などを数値で定量的で表すだけでなく,誤差や不確かさまで定量的に表すべきだと考えています.誤差について理論的な追求はしていないので,ツッコミどころ満載かもしれませんが,何かのお役に立てれば幸いです.
ここまで読んで頂きありがとうございました!次回アドベントカレンダーの投稿は、@ayanerv_2045さんです.
おまけ
PyMC3による確認
上手く分布や標準偏差が推定できているかを確認するため,先程の確率分布と同じものをPyMC3を使用して推定してみます.
!pip install pymc3
import pymc3 as pm
n, cv = data.shape[0], data.sum()
print(n, cv)
with pm.Model() as model:
theta = pm.Uniform('data', lower=0, upper=1, shape=1)
obs = pm.Binomial('DATA', p=theta, n=[n], observed=[cv])
trace = pm.sample(1000, chains=1)
pm.traceplot(trace, figsize=(16, 4))
HDIを標準偏差に合わせてみました.
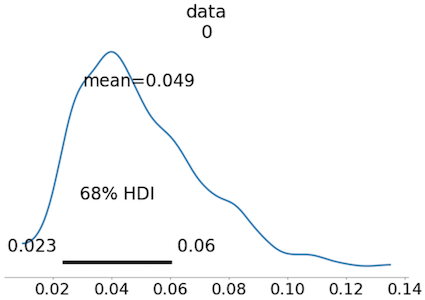
pm.plot_posterior(trace, figsize=(10, 6), hdi_prob=0.6827)
1000件程度のサンプル数だと生成されるデータの分布に違いが出るので,平均も0.5%ほど違いますね,,,標準偏差も算出してみます.
float(trace['data'].std())
0.021
plt.figure(figsize=(10, 6))
sns.histplot(trace['data'], bins=12, stat='probability', label='pymc3')
sns.histplot(means, bins=12, stat='probability', label='sampling')
plt.legend()
plt.show()
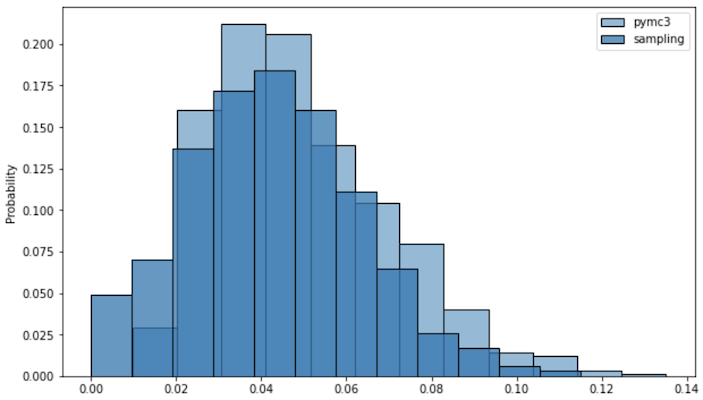
データが異なるため分布に若干の違いは出ますが,似た分布が推定できていることが分かるかと思います.そもそも得られたデータが113件なので,誤差の誤差も大きそう,,,
スプレッドシート
短時間で出来る限りを再現してみました,,,多分エクセルでも殆ど同じ関数で行けると思われます.
BigQuery
そのまま実行すればOK.
既知
WITH data AS (
SELECT
ARRAY<STRUCT<target FLOAT64, sample FLOAT64>>[
(1, 0.9),
(2, 1.7),
(3, 3.12),
(4, 3.87),
(5, 5.02)
] AS values,
)
SELECT
ROUND(AVG(ABS(sample - target)), 3) AS mae,
ROUND(SQRT(AVG(POW(sample - target, 2))), 3) AS rmse,
FROM data,
UNNEST (data.values) AS value
| mae | rmse |
|---|---|
| 0.134 | 0.162 |
WITH data AS (
SELECT
ARRAY<STRUCT<target INT64, sample INT64>>[
(0, 0),
(0, 0),
(1, 1),
(1, 1),
(0, 1),
(1, 1)
] AS values,
)
SELECT
ROUND(SUM(IF(sample = target, 1, 0)) / COUNT(1), 3) AS accuracy,
FROM data,
UNNEST (data.values) AS value
| accuracy |
|---|
| 0.833 |
未知
WITH data AS (
SELECT
[
3.948, 4.42, 3.81, 4.219, 4.03,
4.1, 3.97, 4.35, 3.7, 3.9
] AS sample_values,
)
SELECT
ROUND(STDDEV_SAMP(sample_value), 3) AS stddev_samp,
ROUND(STDDEV_POP(sample_value), 3) AS stddev_pop,
FROM data,
UNNEST (data.sample_values) AS sample_value
| stddev_samp | stddev_pop |
|---|---|
| 0.23 | 0.219 |
左が標本の標準偏差,右が母集団の標準偏差です.