Vol.1: データ構造の概要
この版ではデータ構造の必要性とデータ構造の性能測定方法について学びます。
データ構造の必要性
👌 データを効果的に保存し、処理する方法について正しく理解する必要があります。
👌 資料構造をきちんと理解しないと、不要にメモリと性能を無駄遣いする余地があります
例)
プログラム内でINT型データが100万個ほど使われると仮定した場合、必要なデータを最も素早く探せる資料構造とは何でしょう?
基本的なデータ構造
📌 線形構造
- 配列
- 連結リスト
- スタック
- キュー
📌 非線形構造
- ツリー(Tree)
- グラフ(Graph)
データ構造とアルゴリズムの相関関係
👌 効率的なデータ構造設計のためにアルゴリズム知識が必要です。
👌 効率的なアルゴリズムを作成するためには、問題の状況に応じた適切なデータ構造が使用されなければなりません。
👌したがってデータ構造論とアルゴリズム理論はすべて同一線上に置くことができます。
プログラムの性能測定方法論
👌 時間複雑度(Time Complexity)とは、アルゴリズムに使用される演算回数を意味します。
👌 空間複雑度(Space Complexity)とは、アルゴリズムに使用されるメモリの量を意味します。
→ 効率的なアルゴリズムを使用すると仮定すると、一般的に時間と空間は反比例の関係です。
時間複雑度を表現するときは、最悪の場合を表すBig-O表記法を使います。
複雑度の場合、数学的にも表記が可能です。プログラムを作成する際は最悪の場合を算定して作成しなければならないので、このようにBig-O表記法を使用して最悪の場合をベースにした場合、どれくらいかかるのかと明示することができます。
**例1)次のアルゴリズムはO(n)**の時間複雑度を持ちます。
🖍O(n) = 変数分繰り返すの意味で理解
int main(void)
{
int a, b;
cin >> a >> b;
int sum =1;
for (int i = 0; i < b; i++)
{
sum *= a;
}
cout << sum;
}
**例2)次のアルゴリズムはO(n²)**の時間複雑度を持ちます。
# include<iostream>
using namespace std;
int main(void)
{
int n;
cin >> n;
for (int i = 0; i < n; i++)
{
for(int j =0; j<= i; j++){
cout << "*";
}
cout << '\n';
}
}
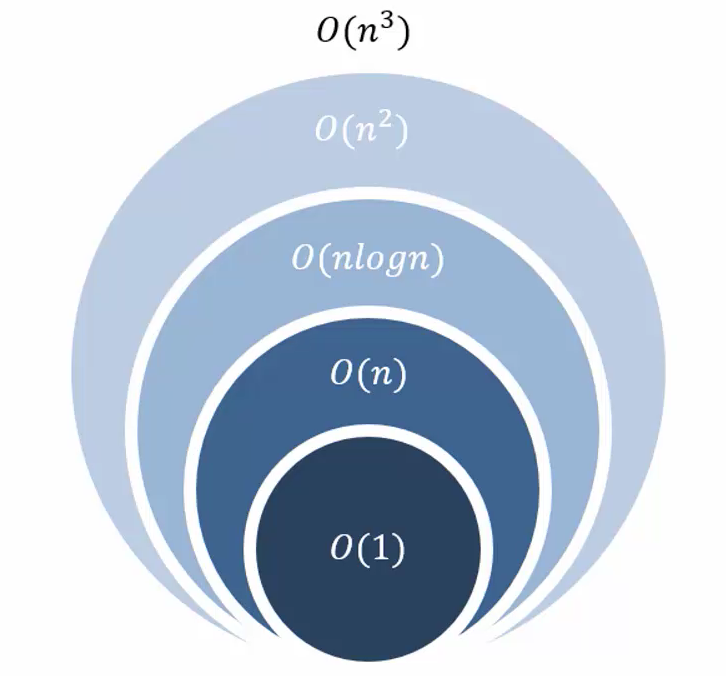
🤔 上の図のようにOの1からnの数乗まで伸ばす方法で多様なアルゴリズムの性能測定が可能です。
例) nが1000だと仮定
↓↓↓↓↓↓↓ Your content
n : 1,000回の演算
nlogn : 約10,000回の演算
n² : 1,000,000回の演算
n³ : 1,000,000,000回の演算
通常、演算回数が10億を超えると1秒以上の時間がかかります。
現実世界の様々な問題では、時間制限が1秒だと考えればいいです。
つまり、あるモジュールが1秒を超えると、事実上ユーザーの立場では多くの時間がかかると感じることができるからです。
また、時間の複雑度を表記するときは、常に大きな項と係数のみ表示します。
例)
O(3n²+n) = O(n²)
空間複雑度を表記するときは、一般的にMB単位で表記します。
例)
int a[1000]:4KB
int a[1000000]:4MB
int a[2000][2000]:16MB
→ int型は4byteの空間を占めるので、int型変数が1000個入る変数を作ったなら、4byte X 1000 = 4000byte = 4KB
📚参考講義:コンピューター工学専攻必須オールインワンパッケージOnline
👆 上記の講義はCとC++を言語を前提に説明しています。