LoginSignup
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@nyosaki

Android で方角センサーを使うときの座標について

Posted at

Android で方角センサーを使うときの座標について

rotation matrix とか remap とか

🌒️ 序

方角って、簡単に手に入ると思っていたのだけれど、実際にはスマホの傾きとかに応じて計算しないといけないことがわかった。とりあえず調べたことを記録しておく。

🌕️ 破

デバイス座標

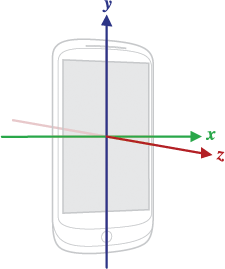
スマホの方角センサーは、スマホに張り付いた座標系で動作している。

Android では、スマホを通常の縦持ち (portrait) した状態で、画面中央から右端に向かって x 軸、画面中央から上端に向かって y 軸、画面に鉛直にスマホを見ている私に向かって z 軸としている。画面が x-y 平面となる。

センサーから直接拾える情報は、この座標系に基づいている。これをデバイス座標 (device coordinate) と呼ぶ。

ここの Figure 1 がわかりやすい。

Figure 1. Coordinate system (relative to a device) that's used by the Sensor API.

世界座標

私たちは、スマホの上ではなく地球の上で生きているので、実際に知りたいのは、スマホに固定された座標上での情報ではなく、地球上での方位情報だ。スマホは磁力と重力をセンサーで読み取って利用しているので、スマホが測っているのは、この2つの方向だ。これを地球上の Y, Z 軸として利用する。

地球は球体なので、地表面を平面地図として便宜上展開する際には、現在地を中心に考える。私が立っている場所が世界の中心であり、東が X 軸、北が Y 軸、足から頭の方向つまり高さが Z 軸となる。

これを世界座標 (world coordinate) と呼ぶ。

世界座標の軸とスマホのデバイス座標の軸を一致させるには、水平な机上にスマホを画面が見えるように置き、上端を北に向ければよい。

方角センサー

スマホの方角センサーは、世界座標に対するデバイス座標のズレを示している。スマホを水平にし、上側を北に向ければ、ズレは 0 だ。このとき、 azimuth = 0, pitch = 0, roll = 0 を示す。スマホの上側を東に向ければ、 azimuth = 90 degree を示す。

SensorManager.remapCoordinateSystem

目的や利用方法により、デバイス座標が扱いにくいことがある。

たとえば、写真を撮るときのようにスマホを立てた状態で、北から東に向きを変えてみた場合、スマホの上側は常に天頂を向いており、北方向とのズレといった場合に、何を示しているのかわからない。

球面極座標の北極と南極では方位角が定まらないのと同じ理屈だ。

特異点付近では計算値の信憑性が失われるので、それを避けるために、安全な座標系を使いたい。方位角を見たいなら、デバイスが動く回転軸を世界座標の Z 軸になるべく近くしておくと良い。

スマホを立てて回すなら、デバイス座標の y 軸が z 軸になったかのように変換すれば、世界座標の Z 軸回りの回転と同じだ。

remapCoordinateSystem(inR, AXIS_X, AXIS_Z, outR)

このとき新 y 軸は、リアカメラ目線の方向になる。なので、リアカメラを向けた方向と北のズレが azimuth として得られる。

rotate

Auto-rotate を on にしたスマホだと、縦持ちや横持ちなどの向きに応じて画面が回転する。これにより上下左右の感覚が変わるので、方向というものの主観的基準に影響する。しかし、これはなるべく切り離して考えるのが良いと思われる。利用者への見せ方という、 ui design の一部であって、センサーの計算の本質を変えるものではない。

実際に使うとなると、、、

ここまでに書いたものは、ネットで得られる情報、つまり参考資料から得た知識を整理しただけだ。
この先、実際に使うとなると、何かと不足している。

  • どのように変換軸を選ぶといいのか？
  • 動いていく中で、いつ切り替えるのがいいのか？

こういう情報はほとんど得られなかった。唯一、次の質問で交わされている議論が一歩踏み込んだものだ。

正解が無い問題だ。用途だったり、利用者との約束事などで変わってくるものだから。スマホを寝かすか立てるか、みたいなものが影響するし、そのときに何が期待されているかにもよる。何より、利用者の主観や好みに左右される。同じ人が同じように横にしたとしても、見たい方向を変えるつもりで横にした場合もあれば、狭い空間に入れるために横にしただけで方向が変わるのを期待していない場合もあるだろう。

まずは、手元で軸変換した結果をいくつか検証してみることにする。

スマホ縦回転

スマホ縦持ち (portrait) で、底辺を軸として回転させる。 Auto-rotate は off もしくは働かない。

1時の方角に配置してみる。北から東に向かって30度の方角だ。

0 degree: 水平表

画面が見える状態で机の上にスマホを置いた状態。

ここで方位角が画面に表示されていたら、多くの人が、スマホ上端が向いている方向だと受け取るだろう。

  • 軸変換
    • 引数X: AXIS_X
    • 引数Y: AXIS_Y

デバイス座標を無変換でそのまま使う。

  • 方位角など
    • azimuth: 34 degree
    • pitch: 0 degree
    • roll: 1 degree

期待したとおり、ほぼ 30 に近い方位角になった。 4 という誤差は、その程度のものと考えてほしい。手で適当において、適当に回転させるのだ。注目したいのは数値の妥当性であり、正確性ではない。

画面を自分に向けるように上端を少し持ち上げると pitch が - に。逆に下げると + に。右端を持ち上げると roll が - に。左端を持ち上げると + に。

90 degree: 垂直正置

写真を撮るときのようにスマホを構えている状態。

多くの人が方位角を、リアカメラが捉えている景色の方向だと受け取るだろう。

  • 軸変換
    • 引数X: AXIS_X
    • 引数Y: AXIS_Z
  • 方位角など
    • azimuth: 17 degree
    • pitch: 0 degree
    • roll: 0 degree

誤差 13 だが許容範囲だ。

  • 無変換の数値
    • azimuth: 97 degree
    • pitch: -88 degree
    • roll: 47 degree

azimuth と roll は不定値と言ったほうがいいだろう。ここで意味のあるのは pitch で、 -90 degree (-1.57 radian) に近い数値を示している。

首を左にかしげて、スマホの角度をそれに合わせれば、 roll が - に。右にかしげたら + に。

180 degree: 水平裏

垂直に構えて持った状態から、思いっきりシート背面を倒して寝てしまった状態。

2つの主観が生じる。

  • リクライニングしただけだから、垂直に持っていたときと同じ方向を期待する。つまり、画面下端方向。
  • 途中経過を破棄して、純粋に、今の上端方向を期待する。

実はもう一つ、天井を見るために寝たのだから天井方向を期待する、という主観もあるはずだが、今は方位角に着眼しているので、高さ方向は排除する。

  • 軸変換

    • 引数X: AXIS_X
    • 引数Y: AXIS_MINUS_Y

  • 方位角など

    • azimuth: 18 degree
    • pitch: 0 degree
    • roll: -3 degree

  • 軸変換

    • 引数X: AXIS_X
    • 引数Y: AXIS_Y

  • 方位角など

    • azimuth: -161 degree
    • pitch: 0 degree
    • roll: -177 degree

誤差 12 および 11 は許容範囲だ。

後者（無変換）での、 pitch 0, roll -180 が、水平裏状態を示している。

右端を持ち上げると roll が - に。左端を持ち上げると + に。これは水平表のときと同じだが、自分の目線で相対的に見ると逆の動きに見える。

pitch について、前者と後者で符号が逆転した動きになる。

270 degree: 垂直倒置

垂直に構えて持った状態から、バックブリッジして、スマホの上端を地面側にして画面を見ている状態。

通常は rotate せず、アプリの ui も地面側を上にしている。

このとき、方位角に着眼すると2つの主観が生じる。

  • たまたまバックブリッジしただけなので、足のつま先が向いている方向が知りたい。

  • 今見ている画面の、リアカメラが捉えている方向が知りたい。

  • 軸変換

    • 引数X: AXIS_X
    • 引数Y: AXIS_MINUS_Z

  • 方位角など

    • azimuth: 24 degree
    • pitch: 1 degree
    • roll: 2 degree

  • 軸変換

    • 引数X: AXIS_X
    • 引数Y: AXIS_Z

  • 方位角など

    • azimuth: -156 degree
    • pitch: 1 degree
    • roll: -178 degree

誤差 6 は許容範囲だ。

  • 無変換の数値
    • azimuth: -87 degree
    • pitch: 87 degree
    • roll: 113 degree

pitch が 90 degree に近いことが、垂直倒置を示している。

首を左にかしげて、スマホの角度をそれに合わせれば、 roll が - に。右にかしげたら + に。垂直正置と同じだが、地面との関係でみたら逆に見える。

スマホ横回転

スマホ横持ち (landscape) で、表示上の底辺（本体の左端）を軸として回転させる。 Auto-rotate は on 。開始時の画面表示が横 (Surface.ROTATION_90) になっているものとする。

1時の方角に配置してみる。北から東に向かって30度の方角だ。

0 degree: 水平表 Surface.ROTATION_90

画面が見える状態で机の上にスマホを置いた状態。

ここで方位角が画面に表示されていたら、多くの人が、画面 ui 上の上端、つまり本体の右端が向いている方向だと受け取るだろう。

  • 軸変換

    • 引数X: AXIS_Y
    • 引数Y: AXIS_MINUS_X

  • 方位角など

    • azimuth: 30 degree
    • pitch: 0 degree
    • roll: 0 degree

  • 無変換の数値

    • azimuth: -59 degree
    • pitch: 0 degree
    • roll: 0 degree

画面を自分に向けるように表示上端（本体右端）を少し持ち上げると pitch が - に。逆に下げると + に。表示右端（本体下端）を持ち上げると roll が - に。左端を持ち上げると + に。

90 degree: 垂直正置 Surface.ROTATION_90

写真を横長で撮るときのようにスマホを構えている状態。

多くの人が方位角を、リアカメラが捉えている景色の方向だと受け取るだろう。

  • 軸変換

    • 引数X: AXIS_Z
    • 引数Y: AXIS_MINUS_X

  • 方位角など

    • azimuth: 33 degree
    • pitch: 0 degree
    • roll: 0 degree

  • 無変換の数値

    • azimuth: -56 degree
    • pitch: 0 degree
    • roll: -90 degree

首を左にかしげて、スマホの角度をそれに合わせれば、 roll が - に。右にかしげたら + に。

180 degree: 水平裏 Surface.ROTATION_90

垂直に構えて持った状態から、思いっきりシート背面を倒して寝てしまった状態。

portrait の場合と同様に2つの主観が生じる。が、今回は、表示の上端方向のみを考えることにする。理由は、 auto-rotate だ。画面が自動回転することで、利用者は画面表示の方向を優先すべきという暗黙のルールに囚われる。

よって、7時の方角。南から西に30度の方角だ。

  • 軸変換

    • 引数X: AXIS_Y
    • 引数Y: AXIS_MINUS_X

  • 方位角など

    • azimuth: -148 degree
    • pitch: -1 degree
    • roll: -178 degree

  • 無変換の数値

    • azimuth: -46 degree
    • pitch: 3 degree
    • roll: -179 degree

270 degree: 垂直倒置 Surface.ROTATION_270

垂直に構えて持った状態から、バックブリッジして、スマホの右端を地面側にして画面を見ている状態。

Auto-rotate により、画面表示は正置となる。リアカメラが捉える方向が期待される。

  • 軸変換

    • 引数X: AXIS_MINUS_Z
    • 引数Y: AXIS_X

  • 方位角など

    • azimuth: -150 degree
    • pitch: 1 degree
    • roll: 0 degree

  • 無変換の数値

    • azimuth: -59 degree
    • pitch: 0 degree
    • roll: 89 degree

180 degree: 水平裏 Surface.ROTATION_270

バックブリッジから水平裏状態に戻すと、今度は表示の上端が逆になる。

よって、1時の方角。北から東に30度の方角だ。

  • 軸変換

    • 引数X: AXIS_MINUS_Y
    • 引数Y: AXIS_X

  • 方位角など

    • azimuth: 34 degree
    • pitch: 1 degree
    • roll: -179 degree

  • 無変換の数値

    • azimuth: -50 degree
    • pitch: -2 degree
    • roll: -178 degree

15, 30, 45, 60, 75 degree

遷移を判断したいので、細かく刻んでみる。水平から垂直までの第1象限だけを見れば十分だ。

  • 15 degree
    • 水平表
      • 軸変換
        • 引数X: AXIS_X
        • 引数Y: AXIS_Y
      • 方位角など
        • azimuth: 30 degree
        • pitch: -15 degree
        • roll: 0 degree
    • 垂直正置
      • 軸変換
        • 引数X: AXIS_X
        • 引数Y: AXIS_Z
      • 方位角など
        • azimuth: 33 degree
        • pitch: 74 degree
        • roll: -2 degree
  • 30 degree
    • 水平表
      • 軸変換
        • 引数X: AXIS_X
        • 引数Y: AXIS_Y
      • 方位角など
        • azimuth: 30 degree
        • pitch: -30 degree
        • roll: 0 degree
    • 垂直正置
      • 軸変換
        • 引数X: AXIS_X
        • 引数Y: AXIS_Z
      • 方位角など
        • azimuth: 28 degree
        • pitch: 59 degree
        • roll: 2 degree
  • 45 degree
    • 水平表
      • 軸変換
        • 引数X: AXIS_X
        • 引数Y: AXIS_Y
      • 方位角など
        • azimuth: 30 degree
        • pitch: -45 degree
        • roll: -1 degree
    • 垂直正置
      • 軸変換
        • 引数X: AXIS_X
        • 引数Y: AXIS_Z
      • 方位角など
        • azimuth: 34 degree
        • pitch: 45 degree
        • roll: 0 degree
  • 60 degree
    • 水平表
      • 軸変換
        • 引数X: AXIS_X
        • 引数Y: AXIS_Y
      • 方位角など
        • azimuth: 33 degree
        • pitch: -58 degree
        • roll: 0 degree
    • 垂直正置
      • 軸変換
        • 引数X: AXIS_X
        • 引数Y: AXIS_Z
      • 方位角など
        • azimuth: 30 degree
        • pitch: 30 degree
        • roll: 0 degree
  • 75 degree
    • 水平表
      • 軸変換
        • 引数X: AXIS_X
        • 引数Y: AXIS_Y
      • 方位角など
        • azimuth: 32 degree
        • pitch: -73 degree
        • roll: 4 degree
    • 垂直正置
      • 軸変換
        • 引数X: AXIS_X
        • 引数Y: AXIS_Z
      • 方位角など
        • azimuth: 30 degree
        • pitch: 15 degree
        • roll: 0 degree

この範囲なら、どちら側に寄せて使っても問題はなさそうだ。本当に特異点に近いところだけ気をつければいいということになる。それで、もっとも単純な作戦としては、中間の 45度で切り替えるというものだろう。

rotation matrix

のちほど参照するために、まとめておく。

縦横の違いはあるが、飛行機（あるいは船舶）における yaw, pitch, roll が rotation matrix と同じ概念なので、ここの絵は理解を助けてくれる。

3軸の任意回転を数式にしたものが記載されている。

R

= R_{device-azimuth} R_{device-roll} R_{device-pitch}

= R_{yaw} R_{pitch} R_{roll}

= R_z(\alpha) R_y(\beta) R_x(\gamma)

=
\begin{pmatrix}
cos(\alpha) & -sin(\alpha) & 0 \\
sin(\alpha) & cos(\alpha) & 0 \\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
cos(\beta) & 0 & sin(\beta) \\
0 & 1 & 0 \\
-sin(\beta) & 0 & cos(\beta)
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 \\
0 & cos(\gamma) & -sin(\gamma) \\
0 & sin(\gamma) & cos(\gamma)
\end{pmatrix}

=
\begin{pmatrix}
cos(\alpha) cos(\beta) & cos(\alpha) sin(\beta) sin(\gamma) - sin(\alpha) cos(\gamma) & cos(\alpha) sin(\beta) cos(\gamma) + sin(\alpha) sin(\gamma) \\
sin(\alpha) cos(\beta) & sin(\alpha) sin(\beta) sin(\gamma) + cos(\alpha) cos(\gamma) & sin(\alpha) sin(\beta) cos(\gamma) - cos(\alpha) sin(\gamma) \\
-sin(\beta) & cos(\beta) sin(\gamma) & cos(\beta) cos(\gamma)
\end{pmatrix}

3行目の要素には $\alpha$ が含まれない。つまり、方位角に依らず、スマホの傾きがどうなっているかを大雑把に知る目安となる。

3行1列の要素 $-\sin(\beta)$ は、 y 軸まわりの回転を示し、飛行機においては pitch だが、スマホのデバイス座標では roll を示している。水平のときに 0 。鉛直のとき、右側（電源ボタン）が下なら -1 、上なら 1 。

3行2列の要素 $\cos(\beta) \sin(\gamma)$ は、 roll と pitch の組み合わせになる。スマホが鉛直のときに、 orientation 相当（ui の動きにかかわらず、スマホ本体の向き）の指標になる。 portrait のときに、正置なら 1 倒置なら -1 。 landscape のときに 0 。

3行3列の要素 $\cos(\beta) \cos(\gamma)$ は、スマホが水平表のときに 1 となる。水平裏のときに -1 。縦横斜め関係なく、スマホ画面が鉛直のとき、つまりカメラが水平方向を向いているときに 0 となる。

現実的なパターン

いくつか挙げてみる。

リアカメラが捉えている方位角を知りたい

おそらく、もっとも判りやすい例だろう。

デバイス座標の z 軸だけを考えれば良い。実際には、 -z が向いている方位だ。

  • 画面に対して鉛直の方向なので、スマホの上下左右に依存しない

  • カメラは物理デバイスなので、画面 ui の向きに依存しない

  • 軸変換

    • 引数X: AXIS_X
    • 引数Y: AXIS_Z

Pitch にも roll にも興味ないなら、常にこの変換結果を見れば良い。

ただし、カメラが天頂および地球の中心を向いているときに、方位角は不定となり、その周辺では表示が不安定になる。

不安定な領域の判定には、軸変換前の原始 rotation matrix の 3行3列要素 (index = 8) の絶対値を見ると良い。これが閾値以上のときに、方位が不安定とのメッセージを画面に出す。閾値は目的により変わってくると思うが、たとえば、 0.7 以上で黄色信号 0.9 以上で赤信号、 0.85 以上で黄色信号 0.95 以上で赤信号、などが考えられる。ちなみに portrait で左右に傾けず持っているなら $\beta = 1$ なので、 $\arccos(0.7) = 0.795 radian = 45.6 \degree$ なので、カメラには地面しか映らない程度になっている。

先の実測で、天頂から $15 \degree$ 程度離れたら azimuth が十分に機能することを確認できているので、実際には $\cos(15 \degree) = 0.966$ あたりまでは余裕ということになる。

仮にカメラと併用しての方位角利用なら、映っている対象物でおおまかな仰角は把握できているはずだから、ごく狭い天頂付近だけ控えめなアラームを出せば良いと思われる。

画面 ui 上での上端方向が知りたい

画面 rotation のみで軸を切り替える。画面 rotation はスマホの傾きに対し、少し遅れて反応するし、同じ傾きでもこれまでの経緯に応じて異なる rotation だったりする。

  • Surface.ROTATION_0
    • 軸変換
      • 無変換
  • Surface.ROTATION_90
    • 軸変換
      • 引数X: AXIS_Y
      • 引数Y: AXIS_MINUS_X
  • Surface.ROTATION_180
    • 軸変換
      • 引数X: AXIS_MINUS_X
      • 引数Y: AXIS_MINUS_Y
  • Surface.ROTATION_270
    • 軸変換
      • 引数X: AXIS_MINUS_Y
      • 引数Y: AXIS_X

ROTATION_180 は、デフォルトで切り替わる機種と抑止されている機種がある。スマホだと使われなくて、タブレットで使われることが多いようだ。

基本はリアカメラ方向が欲しいのだが、水平表にしたときだけ端末の上端方向が知りたい

先のリアカメラ目線のもので、赤信号のときに軸変換を変えてあげればいい。物理上端なので軸変換無しの数値でいい。水平表のみなので、絶対値をとらず 0.9 以上などと正の値のときに水平モードに切り替えれば良い。

🌖️ 急

参考資料

1
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?