量子SVMにおけるFeature mapの可視化 (ブロッホベクトル空間)

量子SVMにおけるFeature map の最適化について、前回の記事
https://qiita.com/notori48/items/86fa9973b584dd4851c9
を更に考察します。
具体的には、Feature map と分離平面の関係を可視化し、データセットにマッチしているかどうか分かるようにしてみます。

以下が参考になります。
https://qiita.com/k43175695/items/1866c1a6f36ddacc60c4
https://arxiv.org/abs/1906.10467

Feature map と分離平面の関係

Feature map から、直接的に分離平面がどうなりそうか予測する方法があります。
https://qiita.com/notori48/items/6367876c3426350fab32

実は量子SVMとは、ブロッホベクトル空間上で分離平面を決めていることに他なりません。
Feature mapは、古典データをブロッホベクトル空間上のどこにマップするかを変えていることに相当します。
なので、ブロッホベクトル空間を調べてやると分離平面がどこを切りそうかわかります。

ブロッホベクトル空間を調べるコード

ゴリ押し実装です。
まず、量子状態ベクトルの密度行列を取ります。

@qml.qnode(dev_kernel)
def density_matrix_of_feature(x1):
    #S(x)
    my_feature_map(x1)
    return qml.density_matrix(wires=range(n_qubits))

続いて、その密度行列からブロッホベクトルを計算するために、ブロッホベクトル空間の基底を用意しておきます。

sigma_0 = (qml.Identity(0) @ qml.Identity(1)).matrix
sigma_1 = (qml.PauliX(0) @ qml.Identity(1)).matrix
sigma_2 = (qml.PauliY(0) @ qml.Identity(1)).matrix
sigma_3 = (qml.PauliZ(0) @ qml.Identity(1)).matrix
sigma_4 = (qml.Identity(0) @ qml.PauliX(1)).matrix
sigma_5 = (qml.PauliX(0) @ qml.PauliX(1)).matrix
sigma_6 = (qml.PauliY(0) @ qml.PauliX(1)).matrix
sigma_7 = (qml.PauliZ(0) @ qml.PauliX(1)).matrix
sigma_8 = (qml.Identity(0) @ qml.PauliY(1)).matrix
sigma_9 = (qml.PauliX(0) @ qml.PauliY(1)).matrix
sigma_10 = (qml.PauliY(0) @ qml.PauliY(1)).matrix
sigma_11 = (qml.PauliZ(0) @ qml.PauliY(1)).matrix
sigma_12 = (qml.Identity(0) @ qml.PauliZ(1)).matrix
sigma_13 = (qml.PauliX(0) @ qml.PauliZ(1)).matrix
sigma_14 = (qml.PauliY(0) @ qml.PauliZ(1)).matrix
sigma_15 = (qml.PauliZ(0) @ qml.PauliZ(1)).matrix

ブロッホベクトルの成分を得るために、密度行列とブロッホベクトル空間の基底の内積を取ります。
内積は、行列積のトレースで定義されています。

def calc_Bloch_vec(Rho):
    Bloch_vec = np.ones((16,1))
    Bloch_vec[0] = np.trace(np.real(np.matmul(Rho, sigma_0)))
    Bloch_vec[1] = np.trace(np.real(np.matmul(Rho, sigma_1)))
    Bloch_vec[2] = np.trace(np.real(np.matmul(Rho, sigma_2)))
    Bloch_vec[3] = np.trace(np.real(np.matmul(Rho, sigma_3)))
    Bloch_vec[4] = np.trace(np.real(np.matmul(Rho, sigma_4)))
    Bloch_vec[5] = np.trace(np.real(np.matmul(Rho, sigma_5)))
    Bloch_vec[6] = np.trace(np.real(np.matmul(Rho, sigma_6)))
    Bloch_vec[7] = np.trace(np.real(np.matmul(Rho, sigma_7)))
    Bloch_vec[8] = np.trace(np.real(np.matmul(Rho, sigma_8)))
    Bloch_vec[9] = np.trace(np.real(np.matmul(Rho, sigma_9)))
    Bloch_vec[10] = np.trace(np.real(np.matmul(Rho, sigma_10)))
    Bloch_vec[11] = np.trace(np.real(np.matmul(Rho, sigma_11)))
    Bloch_vec[12] = np.trace(np.real(np.matmul(Rho, sigma_12)))
    Bloch_vec[13] = np.trace(np.real(np.matmul(Rho, sigma_13)))
    Bloch_vec[14] = np.trace(np.real(np.matmul(Rho, sigma_14)))
    Bloch_vec[15] = np.trace(np.real(np.matmul(Rho, sigma_15)))
    return Bloch_vec

関数の定義が終わったので、グリッド状の古典データ群からブロッホベクトルを計算します。

plt.style.use('default')
fig = plt.figure()

a = np.linspace(-1, 1, 50)
b = np.linspace(-1, 1, 50)
A, B = np.meshgrid(a, b)

C = []
for i in range(50):
    for j in range(50):
        x = np.array([A[i][j].numpy(), B[i][j].numpy()])
        Rho = density_matrix_of_feature(x)
        c = calc_Bloch_vec(Rho)
        C.append(c)

plotします。

C_array = np.array(C)
fig = plt.figure()
for ii in range(16):
    _C = C_array[:,ii].reshape(50, 50)
    ax1 = fig.add_subplot(4, 4, ii+1)
    plt.subplots_adjust(wspace=0.4, hspace=0.6)
    ax1.contourf(A, B, _C, 20, cmap="jet")

plt.show()

論文の再現性を確認

論文
https://arxiv.org/abs/1906.10467
の再現性を確認します。（上記実装があっているか確認します）

論文と同じFeature map にセットします。

def my_feature_map(a):
    for i in range(n_qubits):
        qml.Hadamard(wires=i)
        qml.RZ(a[i], wires=i)
    qml.IsingZZ(np.pi*a[0]*a[1],wires=[0,1])   
    for i in range(n_qubits):
        qml.Hadamard(wires=i)
        qml.RZ(a[i], wires=i)
    qml.IsingZZ(np.pi*a[0]*a[1],wires=[0,1]) 

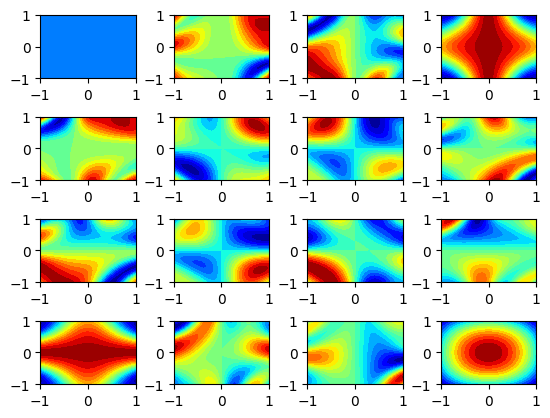
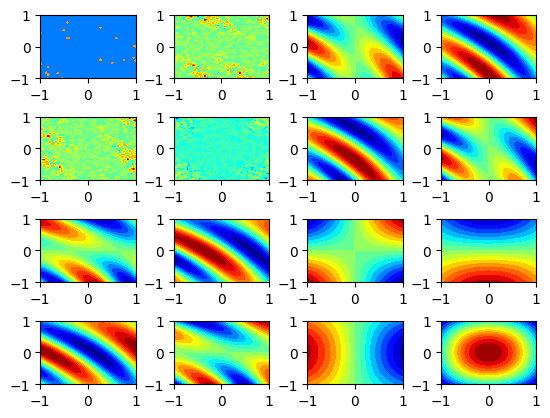
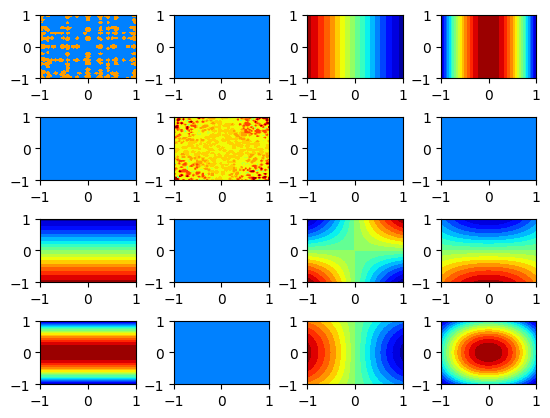
グリッド状の古典データ群に対して、各点のブロッホベクトルの大きさ（色に対応させます）を可視化します。
ブロッホベクトルは全部で16成分あります。

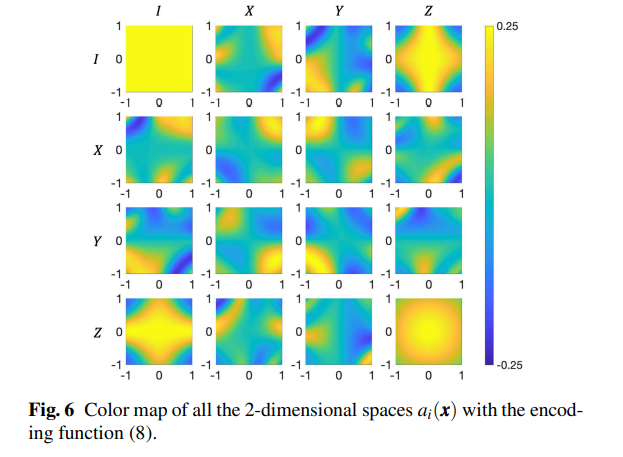
論文の結果は、

上記は一致しています。

この図の見方ですが、例えば(4,4)成分を見てみます。
同心円状になっています。つまりブロッホベクトルの(4.4)成分の大きさは、古典データの半径に比例します。
もし古典データセットがドーナツ状の二値分類だとすると、(4.4)成分のある値を閾値にして分類（つまり(4,4)成分に垂直な平面を分離平面とする)してやれば
きれいに分類できそうだとわかります。
すなわち、ブロッホベクトルの対称性が古典データセットの対称性に近いときは、分離がうまくいきやすいと思えます。

前回の記事の量子SVMを可視化する

前回の記事
https://qiita.com/notori48/items/86fa9973b584dd4851c9

を同じ方法で可視化して分析します。
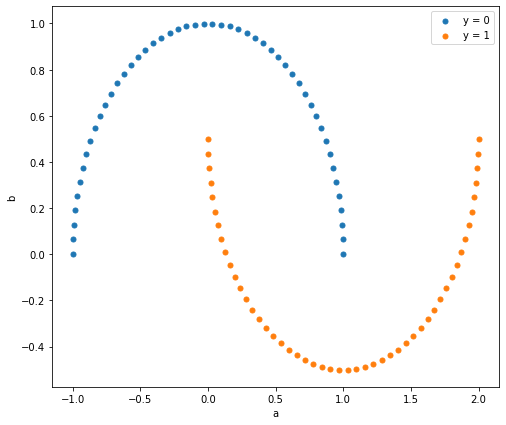
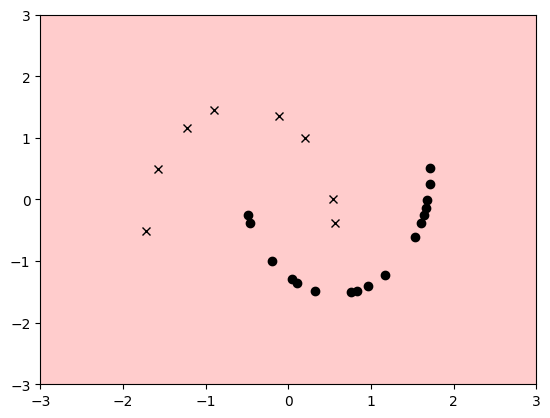
データセットはmoonとします。

これに似た形がブロッホベクトルのどこかに現れれば、そのfeature map は筋が良い（分類性能が高い）と考えられます。

XX feature map (Hadamard抜き)

前回一番良かったfeature map をやってみます。

def my_feature_map(a):
    for i in range(n_qubits):
        qml.RX(a[i], wires=i)
    qml.IsingXX((np.pi-a[0])*(np.pi-a[1]),wires=[0,1])

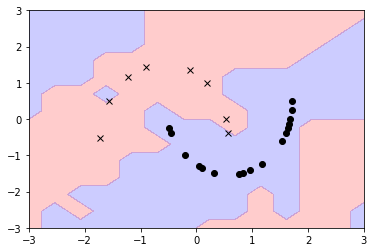
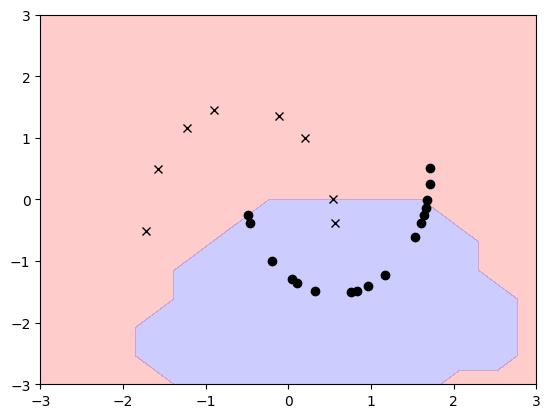
accuracy = 0.96

SVMによる判定領域は以下のようでした。

ではブロッホベクトルはというと、

このようになっています。
moonに似た形・・・というほどのものはないので、筋が良いかは微妙なようです。
しかし、斜めのしましま状の分布がちらほらあります。
そして量子SVMの判定領域も（左右反転してますが？）斜めのしましま状です。
なんとなく一致していて、それっぽいです。

XX feature map (Hadamardあり)

逆に全然駄目だったfeature map はどうなっているのでしょうか。

def my_feature_map(a):
    for i in range(n_qubits):
        qml.Hadamard(wires=i)
        qml.RX(a[i], wires=i)
    qml.IsingXX((np.pi-a[0])*(np.pi-a[1]),wires=[0,1])

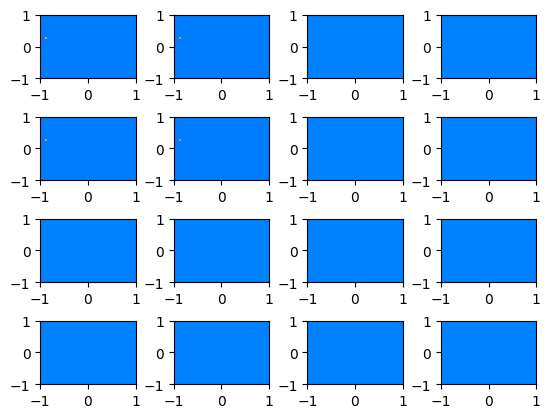
accuracy = 0.32

理由は明らかですね。古典データの値によらずどのブロッホベクトル成分も一定値になってしまっています。
これでは分離ができませんね。

RXゲートのみ

次に1量子ビットゲートのfeature map もみてみます。

def my_feature_map(a):
    for i in range(n_qubits):
        qml.RX(a[i], wires=i)

accuracy = 0.8

いくつかのブロッホベクトル成分の分布を合成すると、SVM判定領域になりそうな気もします。
なお、(1,1)がザリザリしているのは、数値計算誤差だと思います。(1,1)は、純粋状態を扱う限りは必ず一定値を取るはずなので。

まとめ

量子SVMの挙動は、ブロッホベクトル空間を調べると、見えてくる。
しかし、ブロッホベクトル空間を計算する計算量も馬鹿にならないですし、古典データ側も多次元になると
ブロッホベクトルの可視化が事実上できなくなるので、実用性があるかは不明です。。