$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
はじめに
量子サポートベクトルマシン(QSVM)は,サポートベクトルマシン(SVM)に量子計算の概念を導入しようというものです.
本記事では,機械学習の分類問題を考えます.
QSVMでは量子計算を使うにあたって,各サンプル(古典サンプルと呼びます)を量子回路を用いて量子状態に埋め込む必要があります.
一般的に,「どんな量子回路を用いるかで,分類の精度が変化する」ということが知られています.
つまり,量子回路には特有の特徴があると解釈できます.
本記事の目的は,その量子回路の特徴をカラーマップで可視化することです.
※本記事では,この性質の証明とQSVMの具体的なアルゴリズムについての説明は省略します.
これに関しては,[元論文]とこちらの[記事]を参考にしてください.
量子回路を導入する
ここでは,2次元データの2クラス分類を例に挙げて説明します.
QSVMでは,以下の数式で表せる量子回路を初期状態$\ket{0}^{\otimes2}$に作用させることで,古典サンプルを量子状態に埋め込みます.
\rm \mathcal{U}_\Phi(\bf x)\rm = U_\Phi(\bf x)\rm H^{\otimes2}U_\Phi(\bf x)\rm H^{\otimes2} \tag{1}
本記事では,$U_\Phi(\bf x)\rm H^{\otimes2}$のことを単に「量子回路」と呼びます.
以下にイメージを示します.ちなみにRzゲートは任意のZ軸回転を作用させる演算子です.
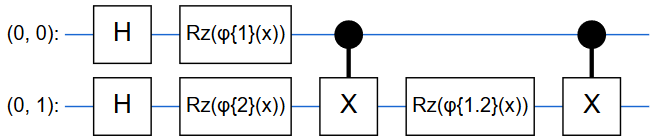
元論文では各Rzゲートの回転角度を,
\{\phi_{\{1\}}(\bf x)\rm=x_1,\phi_{\{2\}}(\bf x)\rm=x_2, \phi_{\{1,2\}}(\bf x)\rm =(\pi-x_1)(\pi-x_2)\} \tag{2}
のようにしていました.
つまり,ここで古典サンプルの情報を量子回路に埋め込んでいることがわかります.
量子状態の特徴をとらえよう
ところで,先ほどの量子回路の持つ特徴とは何でしょうか.
まず,初期状態に(1)を作用させた,$\ket{\Phi(x)} = \mathcal{U}_{\Phi(x)}\ket{0}^{\otimes 2}$の内積$|\braket{\Phi(\bf{x})}{\Phi(\bf{z})}|^2$について考えます.
この内積は古典SVMではカーネルと呼ばれています.つまり,この内積がサンプルの識別境界に影響を与えるものです.
よって,次にその内積が持つ特徴について考えます.先ほどの内積は,密度演算子の性質を用いて,
|\braket{\Phi(\bf{x})}{\Phi(\bf{z})}|^2=2^2\sum_{i=1}^{4^2} a_i(x) a_i(z)
のように変形することが出来ます.(ここでは結果だけ示します.)
つまりこの$a_i$が特徴であ流ことがわかります.
なので,次にこの$a_i$について見ていきます.
$a_i$は,密度演算子$\rho(x) = \ket{\Phi(x)}\bra{\Phi(x)}$が,($\ket{\Phi(x)}$は量子回路を通して得られた状態)
\rho(x) = \sum_{i=1}^{4^2}a_i(x)\sigma_i = \sum_{i=1}^{16}a_i(x)\sigma_i
a_i(x) \in \mathbb{R}, \sigma_i \in P_n = \{I, X, Y, Z\}^2
と変形できる性質を用いて現れたものです.(これは2量子状態の場合です.)
ここで,$\sigma_1, \sigma_2,..., \sigma_{16}$は$II, IX,..., ZZ$です.($I,X,Y,Z$はパウリゲート)
つまり,$a_1(x), a_2(x),...,a_{16}(x)$は,密度演算子をパウリゲートの線形和に表した時の各ゲートの係数でした.
よって古典サンプル$x$の特徴は,量子回路を通して$a_1(x), a_2(x),...,a_{16}(x)$に写像されました.
特徴をカラーマップ化する
一般的に,上で示した特徴$a_1(x), a_2(x),...,a_{16}(x)$は,
a_1 = tr[\rho(x)\sigma_1(x)],a_2 = tr[\rho(x)\sigma_2(x)],...,a_{16} = tr[\rho(x)\sigma_{16}(x)]
のように得ることが出来ます.
そもそも$\rho(x)=\ket{\Phi(x)}\bra{\Phi(x)}$であり,また$\ket{\Phi(x)} = \mathcal{U}_{\Phi(x)}\ket{0}^{\otimes 2}$を満たしていたので,
$\rho(x)$は作用させる(1)によって異なることがわかります.
発想を転換させましょう.
$\rho(x)$は作用させる(1)によって異なる.
-> $\rho(x)$は作用させる量子回路によって異なる.
-> $\rho(x)$によって得られる$a_1(x), a_2(x),...,a_{16}(x)$は作用させる量子回路によって異なる.
-> $a_1(x), a_2(x),...,a_{16}(x)$は量子回路の特徴でもある.
この量子回路の特徴を可視化します.以下は,先ほどの量子回路と位相(2)の場合です.
まず以下のコードで係数$a_1(x), a_2(x),...,a_{16}(x)$を獲得.
def func(x1, x2, i): #2次元データ
x12 = np.cos(x1 + x2) #$\phi{1,2}の位相$
# エンコード回路において,最初に2つのビットそれぞれに作用される位相ゲート
# Rzゲート
U1 = np.array([[1, 0],
[0, np.cos(x1)+1j*np.sin(x1)]])
U2 = np.array([[1, 0],
[0, np.cos(x2)+1j*np.sin(x2)]])
U_2 = np.kron(U1, U2)
# エンコード回路において,CNOTゲートに挟まれる位相ゲート
# Rzゲート
U12 = np.kron(np.array([[1,0], [0,1]]), np.array([[1,0],[0,np.cos(x12) + 1j*np.sin(x12)]]))
#量子回路を通す
##HはアダマールゲートでC_Sは初期状態
F_1 = np.matmul(CNOT, np.matmul(U12, np.matmul(CNOT, np.matmul(U_2, H_2))))
F_2 = np.matmul(F_1, F_1)
C = np.matmul(F_2, C_S)
C_H = np.conjugate(C.T)
C_F = np.matmul(C, C_H)
# 係数の取得
A = np.trace(np.matmul(C_F, np.kron(i[0], i[1])))/4
return A
そしてここで得られた16個の係数のカラーマップを表示します.
plt.style.use('default')
sns.set()
sns.set_style('whitegrid')
sns.set_palette('gray')
np.random.seed(2020)
fig = plt.figure()
for idx, p in enumerate(pair):#pairは\sigma_1, \sigma_2,..., \sigma_{16}のリスト
a = np.linspace(-1, 1, 50)
b = np.linspace(-1, 1, 50)
A, B = np.meshgrid(a, b)
C = []
for i in range(50):
for j in range(50):
c = func(A[i][j], B[i][j], p)
C.append(c)
C = np.array(C).reshape(50, 50)
ax1 = fig.add_subplot(4, 4, idx+1)
plt.subplots_adjust(wspace=0.4, hspace=0.6)
ax1.contourf(A, B, C, 20, cmap="jet")
plt.show()
一番左上が$a_1(x)$で右下が$a_{16}(x)$のカラーマップです.
これで先ほどの量子回路の特徴を捉えることが出来ました.
ここで$a_{16}(x)$のカラーマップに注目してみてください.真ん中が出っ張っています.
つまり,この量子回路は$a_{16}(x)$を特徴として持つため,下ような散らばりを持つデータの分類に有効に働くと言えそうです.

ここの詳細は[Analysis and synthesis of feature map for kernel-based quantum classifier]に示されています.
いろいろな量子回路
先ほどの量子回路が円の概形を散らばりにもつデータの分類に適しているということは示しました.
ここでは,例として二つほど別の量子回路を導入していきます.
一見最初の回路と同じように見えますが,使用している位相ゲートが異なります.
(一つ目がRxゲート,二つ目がRyゲートです.)
またこれらのゲートにおける位相を,
\{\phi_{\{1\}}(\bf x)\rm=x_1,\phi_{\{2\}}(\bf x)\rm=x_2, \phi_{\{1,2\}}(\bf x)\rm =\pi x_1x_2\}
のように設定しました.ここも,さき程と異なります.
この回路が持つ特徴は以下のようになります.

これも使用している位相ゲートが異なります.(一つ目がRyゲート,二つ目がRzゲートです)
これらのゲートにおける位相は,
\{\phi_{\{1\}}(\bf x)\rm=x_1,\phi_{\{2\}}(\bf x)\rm=x_2, \phi_{\{1,2\}}(\bf x)\rm =cos(x_1)cos(x_2)\}
のように設定しました.
この回路が持つ特徴は以下のようになりました.

ここで,$a_9やa_{12}$をみてください.これは,以下のようなデータの分類に適していそうです.

このようにQSVMにおいて,量子回路によって,どんな散らばりを持つデータの分類に適するかが異なることがわかりました.
実際に,moon型のデータの分類を今まで示してきた三つの回路を用いたQSVMで試してみたところ,三つ目の回路を用いた時に精度が良くなりました.
補足
最後にこの量子回路をQSVMにおいて導入するコードを載せておきます.
ベースはこちらの[記事]を参考にさせていただきました.
一番最初の回路はqiskitにライブラリが用意してあります.
feature_map1 = ZZFeatureMap(feature_dim, reps=2)
二つ目の回路は以下のコードで可能です.
class CustomFeatureMap(FeatureMap):
def __init__(self, feature_dimension, depth=2, entangler_map=None):
self._support_parameterized_circuit = False
self._feature_dimension = feature_dimension
self._num_qubits = self._feature_dimension = feature_dimension
self._depth = depth
self._entangler_map = None
if self._entangler_map is None:
self._entangler_map = [[i, j] for i in range(self._feature_dimension) for j in range(i + 1, self._feature_dimension)]
# 回路の構築
def construct_circuit(self, x, qr, inverse=False):
qc = QuantumCircuit(qr)
for _ in range(self._depth):
qc.h(qr[0])
qc.h(qr[1])
qc.rx(x[0], qr[0])
qc.rx(x[1], qr[1])
qc.cx(qr[0], qr[1])
qc.ry(np.pi * x[0] * x[1], qr[1])
qc.cx(qr[0], qr[1])
if inverse:
qc.inverse()
return qc
これをベースモデルの該当箇所に置き換えれば実際にQSVMを動かすことが出来ます.
まとめ
本記事では,QSVMにおける量子回路のもつ特徴をカラーマップを用いて可視化しました.
これにより,様々な散らばりを持つデータの分類に対し,適した量子回路が存在することがわかりました.
これにより,ある特徴的な散らばりを持つデータの分類に対し,それに適した量子回路を意図的に生成できることになります.
これは,古典のSVMにはない興味深い知見であると思います.
この性質を有効に活用することで,古典のSVMに勝るモデルを構築することも可能になると考えます.
#参考サイト
https://qiita.com/ucc_white/items/f2ea0d019979dd675f82



