More than 3 years have passed since last update.

PennyLaneで量子回路学習

Last updated at 2021-04-06Posted at 2021-04-01

PennyLaneで量子回路学習

世にも珍しいPennyLaneの日本語記事です。

量子機械学習に強いPennyLaneで量子回路学習をやってみます。
qiskitで量子回路学習とほぼ同じです。　https://qiita.com/notori48/items/ebfa4a8c8ee2da134ba1

$\sin x$ を学習します。

Code

import系

%matplotlib inline

import pennylane as qml
from pennylane import numpy as np
import matplotlib.pyplot as plt

パラメータ定義とデータ準備

########  パラメータ  #############
nqubit = 3 ## qubitの数
num_layers = 3 # 層数

## [x_min, x_max]のうち, ランダムにnum_x_train個の点をとって教師データとする.
x_min = - 1.; x_max = 1.;
num_x_train = 50

## 学習したい1変数関数
func_to_learn = lambda x: np.sin(x*np.pi)

## 乱数のシード
random_seed = 0
## 乱数発生器の初期化
np.random.seed(random_seed)



#### 教師データを準備
X = x_min + (x_max - x_min) * np.random.rand(num_x_train)
Y = func_to_learn(x_train)

# 現実のデータを用いる場合を想定し、きれいなsin関数にノイズを付加
mag_noise = 0.05
Y = Y + mag_noise * np.random.randn(num_x_train)

X = X
Y = Y/2 # In Pennylane, <x|O|x> can be used as a model output but not 2<x|O|x>. We sclaed the Y instead of the output.
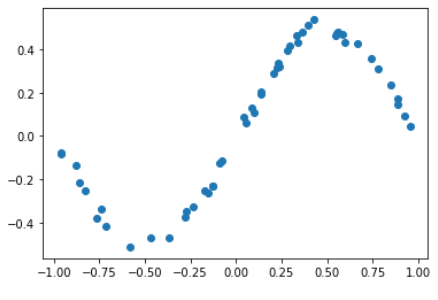
plt.plot(X, Y, "o"); plt.show()

注意点として、PennyLaneではオブザーバブル期待値を定数倍する機能が見当たりません。
このQCLの例(sin x の学習）では、$Z$期待値の2倍程度を表現できないと、学習過程で$f(x)$が飽和して
うまくいきません。
そこで、応急処置として$\sin x$を2で割ってスケーリングしています。
一般の場合は、量子回路の出力に古典NNを繋げてやればいいのでしょうかね。

デバイス定義

dev1 = qml.device("default.qubit", wires=nqubit) # define a device

実機を使うとか、連続量量子計算にするとかはここで指定します。
wire というのは、基本的に量子ビット数を指定しておけば良いようです。

ランダム回路を準備


Jx = -1. + 2.*np.random.rand(nqubit) ## -1~1の乱数
J_ij = -1. + 2.*np.random.rand(nqubit,nqubit)

def add_ZiZj(coeff_pq, p, q):
    qml.CNOT(wires=[p, q])  
    qml.RZ(+2*coeff_pq, wires=p) ## qiskitでは RZ(theta)=e^{-i*theta/2*Z}      
    qml.CNOT(wires=[p, q])


def add_Xi(coeff_p, p):
    qml.RX(+2*coeff_p,wires=p) ## qiskitでは RX(theta)=e^{-i*theta/2*X}      


def add_Zij_Xi():
    for i in range(nqubit): ## i runs 0 to nqubit-1
        add_Xi(Jx[i],i)
        for j in range(i+1, nqubit):
            add_ZiZj(J_ij[i,j], i, j)

PennyLaneにはテンプレートというものがあって、そこに Strongly Entangled とかいう
ランダム回路があります。それを使ってもいいです。

変分回路の定義


def layer(v):
    for i in range(nqubit):
        qml.RX(v[3*i],wires=i)
        qml.RZ(v[3*i+1],wires=i)
        qml.RX(v[3*i+2],wires=i)

    add_Zij_Xi()

データ入力回路の定義


@qml.qnode(dev1)
def quantum_neural_net(var, x):
    angle_y = np.arcsin(x)
    angle_z = np.arccos(x**2)
    for i in range(nqubit):
        qml.RY(angle_y, wires=i)
        qml.RZ(angle_z, wires=i)
  
    # "layer" subcircuits
    for v in var:
        layer(v)
        
    return qml.expval(qml.PauliZ(0))

@qml.qnode(dev1) という記法の意味がぜんぜんわかってません。

ロスとコストの定義


def square_loss(desired, predictions):
    loss = 0
    for l, p in zip(desired, predictions):
        loss = loss + (l - p) ** 2

    loss = loss / len(desired)
    return loss

def cost(var, features, desired):
    preds = [quantum_neural_net(var, x) for x in features]
    return square_loss(desired, preds)

変数の初期値を設定しておきます。

np.random.seed(0)
var_init = 0.05 * np.random.randn(num_layers, 3*nqubit)
print(var_init)

[[ 0.08820262 0.02000786 0.0489369 0.11204466 0.0933779 -0.04886389 0.04750442 -0.00756786 -0.00516094] [ 0.02052993 0.00720218 0.07271368 0.03805189 0.00608375 0.02219316 0.01668372 0.07470395 -0.01025791] [ 0.01565339 -0.04270479 -0.12764949 0.03268093 0.04322181 -0.03710825 0.11348773 -0.07271828 0.00228793]]

最適化

PennyLaneでは勾配降下法が使えます！以下はSGDを使っています。
量子勾配計算のアルゴリズムの説明がいまいち見当たらないのですが、おそらくparameter shift rule だと思います。
back propagation も使えるらしいのですが、使い方を調査中です。

2021/04/06追記
デフォルトがback propagationのようです！
これはqnodeを作るときに　diff_method という引数で明示的に指定できます。


opt = qml.GradientDescentOptimizer(0.1)

var = var_init
for it in range(500):
    var, _cost = opt.step_and_cost(lambda v: cost(v, X, Y), var)
    print("Iter: {:5d} | Cost: {:0.7f} ".format(it, _cost))

学習が終わりました。数分かかります。

qulacsだともっと早いです。parameter shift rule だと勾配計算が重すぎてイマイチですね。

結果の確認

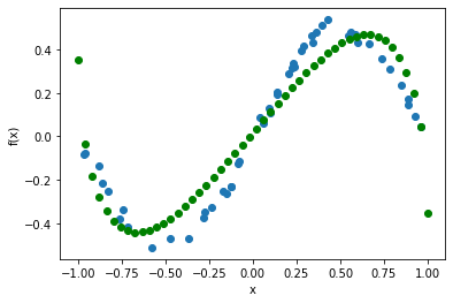
x_pred = np.linspace(-1, 1, 50)
predictions = [quantum_neural_net(var, x_) for x_ in x_pred]
predictions_init = [quantum_neural_net(var_init, x_) for x_ in x_pred]

plt.figure()
plt.scatter(X, Y)
plt.scatter(x_pred, predictions, color="green")

plt.xlabel("x")
plt.ylabel("f(x)")
plt.tick_params(axis="both", which="major")
plt.tick_params(axis="both", which="minor")
plt.show()

学習できています。

まとめ

PennyLaneでQCLを実装した。確かに機械学習に関しては、ライブラリ多いのでかなり短く書けそうでした。
parameter shift rule だと勾配計算自体が重く、勾配法なのに勾配なし最適化に（計算時間で）劣る？ back propagationを使わないといけなさそう
- 追記で書いたとおり、上記はback propagationでの結果でした。それでも重いわけですが、パラメータ数が増えても計算時間が増えにくいという特徴があります。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up