Qiskitで量子回路学習基礎

量子回路学習

Do-jo 5-2の量子回路学習　を例題として、qiskitで書いてみます。

スクリプト

importとか

#必要なモジュールのインポート
from qiskit import IBMQ, QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import execute, Aer
from qiskit.qasm import pi
from qiskit.tools.visualization import plot_histogram, circuit_drawer
from qiskit.quantum_info import Statevector
from qiskit.extensions.simulator.snapshot import snapshot
import matplotlib.pyplot as plt
from functools import reduce
import numpy as np


########  パラメータ  #############
nqubit = 3 ## qubitの数
depth = 1 ## circuitの深さ
time_step = 0.77  ## ランダムハミルトニアンによる時間発展の経過時間

## [x_min, x_max]のうち, ランダムにnum_x_train個の点をとって教師データとする.
x_min = - 1.; x_max = 1.;
num_x_train = 50

## 学習したい1変数関数
func_to_learn = lambda x: np.sin(x*np.pi)

## 乱数のシード
random_seed = 0
## 乱数発生器の初期化
np.random.seed(random_seed)

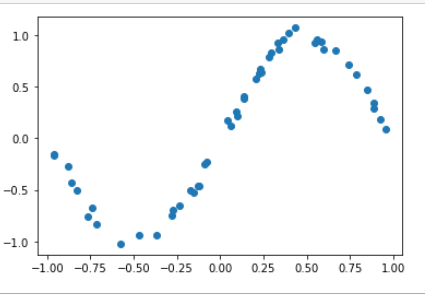
#### 教師データを準備
x_train = x_min + (x_max - x_min) * np.random.rand(num_x_train)
y_train = func_to_learn(x_train)

# 現実のデータを用いる場合を想定し、きれいなsin関数にノイズを付加
mag_noise = 0.05
y_train = y_train + mag_noise * np.random.randn(num_x_train)

plt.plot(x_train, y_train, "o"); plt.show()

以下を学習します。

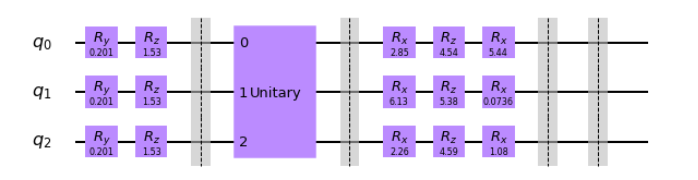
回路図を先に示します。ここではdepth = 1 の例です。

• 初段
  入力データ$x$に依存したゲート操作です。
  入力データを量子状態にマッピングしています。
  なんでも良いと思います。

• 二段目
  表現力を上げるためのランダムユニタリゲートです。
  何でも良いと思いますが、Dojoにならって横磁場イジングモデルの時間発展ゲートを使います。
  ただしDo-joと違って、トロッター分解（もどき）で実装してます。
  ハールランダムにSU(N)の元を取ってきても良いはずですが、最悪は単位行列を取ってくる可能性もありますよね。
  そういったことを極力防ぐ意味でイジングモデルのゲートを持ってきている（ただしパラメータはてきとー）のかと思います。

• 最終段
  変分ゲートです。ここのパラメータを調整して、学習させます。
  なんでも良いと(ry

なお、オブザーバブルとして$O = 2 * ( Z \otimes I \otimes I)$をとり、オブザーバブルの期待値を
回路出力とします。このオブザーバブルもなんでも良いと(ry

オブザーバブル

from qiskit.quantum_info.operators import Operator, Pauli
pauli0 = Pauli(label='ZII')

obs_op = 2*(Operator(pauli0))
obs_mat = obs_op.data
print(obs_mat)

$$
O = 2 * ( Z \otimes I \otimes I)
$$

回路

xをエンコードするゲートを作成する関数

def add_xin(circuit_in, x_in):
    angle_y = np.arcsin(x_in)
    angle_z = np.arccos(x_in**2)
    for i in range(nqubit):
        circuit_in.ry(angle_y,i)
        circuit_in.rz(angle_z,i)
    circuit_in.barrier()    
    return circuit_in

circuit に $ e^{-ihZ_{i}Z_{i+1}} $ を加える関数

$ e^{-ihZ_{i}Z_{i+1}} = CNOT_{i,i+1} * RZ(2h) * CNOT_{i,i+1} $

def add_ZiZj(circuit_in, coeff_pq, p, q):
    circuit_in.cx(p, q)  
    circuit_in.rz(+2*coeff_pq, p) ## qiskitでは RZ(theta)=e^{-i*theta/2*Z}      
    circuit_in.cx(p, q)
    return circuit_in

circuit に $ e^{-ihX_{i}} $ を加える関数

$ e^{-ihX_{i}} = RX(2h) $

def add_Xi(circuit_in, coeff_p, p):
    circuit_in.rx(+2*coeff_p, p) ## qiskitでは RX(theta)=e^{-i*theta/2*X}      
    return circuit_in

circuit にZZとXをランダムに加える関数

#ランダム磁場・ランダム結合イジングハミルトニアンをつくって時間発展演算子をつくる

def add_Zij_Xi(circuit_in):
    for i in range(nqubit): ## i runs 0 to nqubit-1
        Jx = -1. + 2.*np.random.rand() ## -1~1の乱数
        add_Xi(circuit_in, Jx, i)
        for j in range(i+1, nqubit):
            J_ij = -1. + 2.*np.random.rand()
            add_ZiZj(circuit_in, J_ij, i, j)
    circuit_in.barrier()           
    return circuit_in

ここで、上記回路　 add_Zij_Xi　を毎回やっていると時間かかります。この回路は学習の間は一定なので、行列を取得して定数ゲートにしてしまいます。

circuit = QuantumCircuit(nqubit)
circuit = add_Zij_Xi(circuit)

# Select the UnitarySimulator from the Aer provider
simulator_unitary = Aer.get_backend('unitary_simulator')

# Execute and get counts
result = execute(circuit, simulator_unitary).result()
ZZ_X_mat = result.get_unitary(circuit)
from qiskit.quantum_info.operators import Operator
ZZ_X_gate = Operator(ZZ_X_mat)
print(np.shape(ZZ_X_mat))

変分ROTゲートを加える関数

def add_Variational_Circuit(circuit_in, theta_in, current_depth):
    for j in range(nqubit):
        circuit_in.rx(parameter_vec[3*j+3*nqubit*i+0],j)
        circuit_in.rz(parameter_vec[3*j+3*nqubit*i+1],j)
        circuit_in.rx(parameter_vec[3*j+3*nqubit*i+2],j)
    circuit_in.barrier()           
    return circuit_in

ゲート連結

ゲート要素は揃ったので、連結していきます。2回にわけてますが、一発でもいいです。

def Make_Circuit_1(circuit_in, x_in):  
    circuit_in = add_xin(circuit_in, x_in)
    circuit_in.barrier()
    return circuit_in

def Make_Circuit_2(circuit_in, theta_in): 
    for i in range(depth):
        #circuit = add_Zij_Xi(circuit)
        circuit_in.unitary(ZZ_X_gate, [0,1,2], label = 'ZZ_X')
        circuit_in.barrier()
        circuit_in = add_Variational_Circuit(circuit_in, theta_in, i)
        circuit_in.barrier()
        
    return circuit_in

上記ゲートからオブザーバブル期待値を計算する関数です。

backend = Aer.get_backend('statevector_simulator')
def qcl_pred(x_in, theta_in):
    circuit = QuantumCircuit(nqubit)
    circuit = Make_Circuit_1(circuit, x_in)
    circuit = Make_Circuit_2(circuit, theta_in)    
    circuit.snapshot('my_sv',snapshot_type='statevector') # get a snapshot of present statevector           
    results = execute(circuit, backend, shots=1).result()
    statevec = results.data()['snapshots']['statevector']['my_sv'][0] # 2^nqubits complex vector |ψ>
    expectation = np.real(np.vdot(statevec,np.dot(obs_mat,statevec))) # Real[<ψ|O|ψ>]
    return expectation

オブザーバブル期待値とトレーニングyの差を計算します。（コスト関数）

def cost(theta_in):
    y_pred = [qcl_pred(x, theta_in) for x in x_train]
    # quadratic loss
    L = ((y_pred - y_train)**2).mean()
    return L

初期値

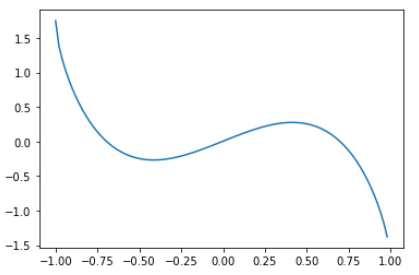
試しに初期パラメータで波形を書いてみます。

# パラメータthetaの初期値のもとでのグラフ
xlist = np.arange(x_min, x_max, 0.02)
y_init = [qcl_pred(x, theta_init) for x in xlist]
plt.plot(xlist, y_init)

もちろん正弦波とは似てもにつきません。
では、学習させます。
一時間ぐらいかかるみたいです。。。

学習

from scipy.optimize import minimize

# 学習 (筆者のPCで数十分程度かかる)
#result = minimize(cost, theta_init, method='Nelder-Mead')
result = minimize(cost, theta_init, method='Powell')

# 最適化後のcost_functionの値
result.fun

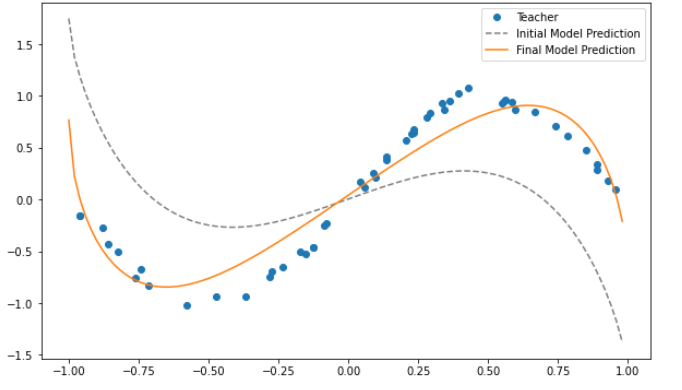
プロットしてみます。

# プロット
plt.figure(figsize=(10, 6))

xlist = np.arange(x_min, x_max, 0.02)

# 教師データ
plt.plot(x_train, y_train, "o", label='Teacher')

# パラメータθの初期値のもとでのグラフ
plt.plot(xlist, y_init, '--', label='Initial Model Prediction', c='gray')

# モデルの予測値
y_pred = np.array([qcl_pred(x, theta_opt) for x in xlist])
plt.plot(xlist, y_pred, label='Final Model Prediction')

plt.legend()
plt.show()

ぼちぼち出来ていますね。1時間かかるっていうのがひどいですね。コーディングの仕方のせいでしょう。

結論

qiskitでも量子回路学習できた。
ランダムゲートとか、Dojoと微妙に変えてるんですが
ちゃんと動いています。