QiskitでQAOA w/勾配降下

Qiskit Gradient Framework

qiskitも勾配を計算するライブラリを出していました。
https://qiskit.org/documentation/tutorials/operators/02_gradients_framework.html

これを使って勾配降下でQAOAをやってみます。

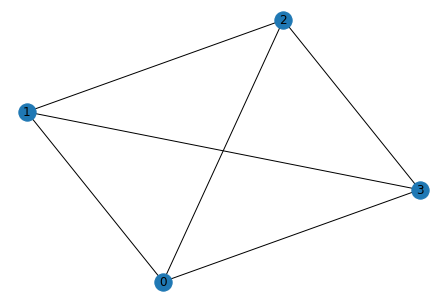
解く問題

4ノードの全結合MAX CUT とします。

ハミルトニアンは以下の形で、最小値は-4です。

(array([ 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, -3. ]),
[PauliZ(wires=[0]) @ PauliZ(wires=[1]),
PauliZ(wires=[0]) @ PauliZ(wires=[2]),
PauliZ(wires=[0]) @ PauliZ(wires=[3]),
PauliZ(wires=[1]) @ PauliZ(wires=[2]),
PauliZ(wires=[1]) @ PauliZ(wires=[3]),
PauliZ(wires=[2]) @ PauliZ(wires=[3]),
Identity(wires=[0])])

実装

#General imports
import numpy as np
#Operator Imports
from qiskit.opflow import Z, X, I, StateFn
from qiskit.opflow.gradients import Gradient
# Execution Imports
from qiskit import Aer
from qiskit.utils import QuantumInstance
# Algorithm Imports
from qiskit.algorithms import VQE
from qiskit.algorithms.optimizers import CG

from qiskit.circuit import QuantumCircuit, ParameterVector
from scipy.optimize import minimize

# Instantiate the system Hamiltonian
h2_hamiltonian = 0.5*(Z^Z^I^I) + 0.5*(I^Z^Z^I) + 0.5*(I^I^Z^Z) + 0.5*(Z^I^I^Z) + 0.5*(Z^I^Z^I) + 0.5*(I^Z^I^Z) -3*(I^I^I^I)

# This is the target energy
h2_energy = -4

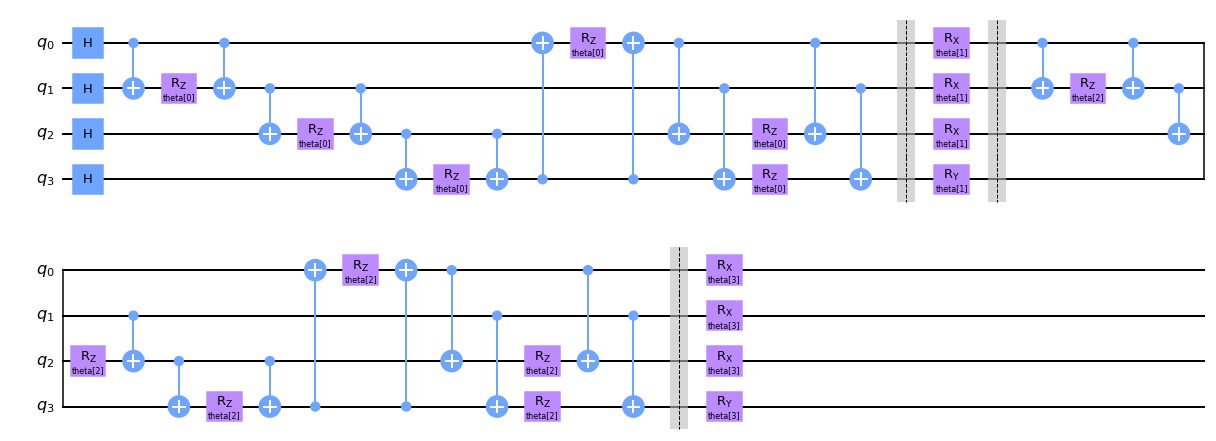
# Define the Ansatz
wavefunction = QuantumCircuit(4)
params = ParameterVector('theta', length=4)
wavefunction.h(range(0,4))
# it = iter(params)
wavefunction.cx(0, 1)
wavefunction.rz(params[0], 1)
wavefunction.cx(0, 1)
wavefunction.cx(1, 2)
wavefunction.rz(params[0], 2)
wavefunction.cx(1, 2)
wavefunction.cx(2, 3)
wavefunction.rz(params[0], 3)
wavefunction.cx(2, 3)
wavefunction.cx(3, 0)
wavefunction.rz(params[0], 0)
wavefunction.cx(3, 0)
wavefunction.cx(0, 2)
wavefunction.rz(params[0], 2)
wavefunction.cx(0, 2)
wavefunction.cx(1, 3)
wavefunction.rz(params[0], 3)
wavefunction.cx(1, 3)
wavefunction.barrier()

wavefunction.rx(params[1], 0)
wavefunction.rx(params[1], 1)
wavefunction.rx(params[1], 2)
wavefunction.ry(params[1], 3)
wavefunction.barrier()

wavefunction.cx(0, 1)
wavefunction.rz(params[2], 1)
wavefunction.cx(0, 1)
wavefunction.cx(1, 2)
wavefunction.rz(params[2], 2)
wavefunction.cx(1, 2)
wavefunction.cx(2, 3)
wavefunction.rz(params[2], 3)
wavefunction.cx(2, 3)
wavefunction.cx(3, 0)
wavefunction.rz(params[2], 0)
wavefunction.cx(3, 0)
wavefunction.cx(0, 2)
wavefunction.rz(params[2], 2)
wavefunction.cx(0, 2)
wavefunction.cx(1, 3)
wavefunction.rz(params[2], 3)
wavefunction.cx(1, 3)
wavefunction.barrier()

wavefunction.rx(params[3], 0)
wavefunction.rx(params[3], 1)
wavefunction.rx(params[3], 2)
wavefunction.ry(params[3], 3)

# Define the expectation value corresponding to the energy
op = ~StateFn(h2_hamiltonian) @ StateFn(wavefunction)

wavefunction.draw('mpl')

2レイヤーのQAOA回路です。

grad = Gradient(grad_method='lin_comb')
# grad = Gradient(grad_method='param_shift')

qi_sv = QuantumInstance(Aer.get_backend('aer_simulator_statevector'),
                        shots=1,
                        seed_simulator=2,
                        seed_transpiler=2)

#Conjugate Gradient algorithm
optimizer = CG(maxiter=1)

# Gradient callable
vqe = VQE(wavefunction, optimizer=optimizer, gradient=grad, quantum_instance=qi_sv)

result = vqe.compute_minimum_eigenvalue(h2_hamiltonian)
print('Result:', result.optimal_value, 'Reference:', h2_energy)

1 teration でもすごく遅く、数分かかっても終わらず。
実用に耐えません。

ちなみにPennylaneで同じ問題を勾配降下(アルゴリズムはbackprop)でやると、50イタレーションでも1秒ぐらいです。

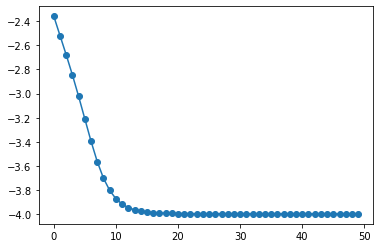
経過時間：1.5399999618530273
Iter: 49 | Cost: -3.9952981
Pennylaneでの実装は以下の記事に書いています。
https://qiita.com/notori48/items/e78b72d196a78ac863c9

まとめ

qiskitのgradien FW を使った勾配最適化は本当に実用的なのだろうか？