そういえばPennylaneでQAOAを勾配降下で解く実装を記事にしていませんでした。
全結合MAX CUT をQAOAで解く
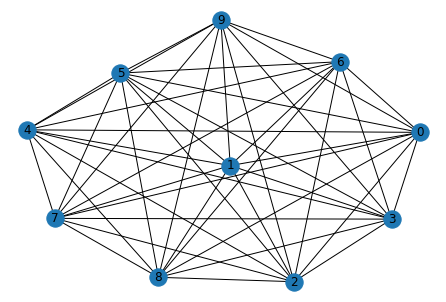
例えば10ノードの全結合グラフのMAX CUT を考えます。
import pennylane as qml
from pennylane import qaoa
from pennylane import numpy as np
from networkx import Graph, erdos_renyi_graph
import matplotlib.pyplot as plt
n_qubits = 10 # number of qubits
n_layers = 1
graph = erdos_renyi_graph(n_qubits, p=1, directed=False)
# Defines the wires and the graph on which MaxCut is being performed
wires = range(n_qubits)
import networkx as nx
nx.draw(graph, with_labels = True)
plt.show()
QAOA Ansatzを組み立てるのに必要なパーツを先に定義します。
# Defines the QAOA cost and mixer Hamiltonians
cost_h, mixer_h = qaoa.maxcut(graph)
# Defines a layer of the QAOA ansatz from the cost and mixer Hamiltonians
def qaoa_layer(gamma, alpha):
qaoa.cost_layer(gamma, cost_h)
qaoa.mixer_layer(alpha, mixer_h)
勾配降下
# Repeatedly applies layers of the QAOA ansatz
dev = qml.device('default.qubit', wires=len(wires))
@qml.qnode(dev,diff_method='backprop')
def cost_function(params, **kwargs):
for w in wires:
qml.Hadamard(wires=w)
qml.layer(qaoa_layer, n_layers, params[0:n_layers,0], params[0:n_layers,1])
return qml.expval(cost_h)
opt = qml.GradientDescentOptimizer(0.01)
hist_cost = []
var_init = np.random.randn(n_layers,2)
var = var_init
import time
# 処理前の時刻
t1 = time.time()
for it in range(10):
var, _cost = opt.step_and_cost(cost_function, var)
print("Iter: {:5d} | Cost: {:0.7f} ".format(it, _cost))
hist_cost.append(_cost)
# 処理後の時刻
t2 = time.time()
# 経過時間を表示
elapsed_time = t2-t1
print(f"経過時間:{elapsed_time}")
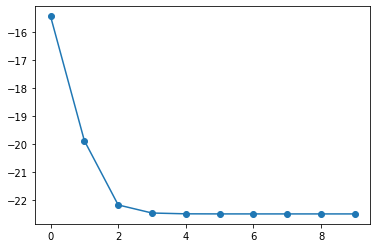
Iter: 0 | Cost: -15.4306719 Iter: 1 | Cost: -19.8801702 Iter: 2 | Cost: -22.1785671 Iter: 3 | Cost: -22.4678397 Iter: 4 | Cost: -22.4965657 Iter: 5 | Cost: -22.4996299 Iter: 6 | Cost: -22.4999601 Iter: 7 | Cost: -22.4999958 Iter: 8 | Cost: -22.4999996 Iter: 9 | Cost: -22.5000000 経過時間:2.244999885559082
plt.plot(hist_cost,'o-')
非勾配
scipy.minimizeで非勾配な最適化をしてみます。
dev = qml.device('lightning.qubit', wires=len(wires))
# Repeatedly applies layers of the QAOA ansatz
@qml.qnode(dev)
def cost_function(var, **kwargs):
var_2d_array = np.reshape(var,(n_layers,2))
for w in wires:
qml.Hadamard(wires=w)
qml.layer(qaoa_layer, n_layers, var_2d_array[0:n_layers,0], var_2d_array[0:n_layers,1])
return qml.expval(cost_h)
from scipy.optimize import minimize
import time
var_init = np.random.uniform(low=-1, high=1, size=(2*n_layers)) # one-dimensional array
hist_cost = []
var = var_init
count = 0
def cbf(Xi):
global count
global hist_cost
cost_now = cost_function(Xi)
hist_cost.append(cost_now)
print('iter = '+str(count)+' | cost = '+str(cost_now))
count += 1
t1 = time.time()
result = minimize(fun=cost_function, x0=var_init, method='Nelder-Mead', callback=cbf, options={"maxiter":11})
# 処理後の時刻
t2 = time.time()
# 経過時間を表示
elapsed_time = t2-t1
print(f"経過時間:{elapsed_time}")
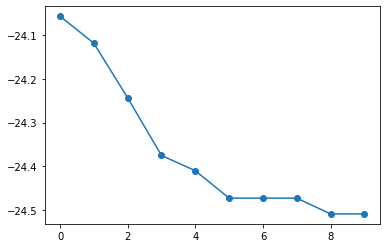
iter = 0 | cost = -24.05773509630845 iter = 1 | cost = -24.119313285482026 iter = 2 | cost = -24.24372585868572 iter = 3 | cost = -24.37502879518174 iter = 4 | cost = -24.40971631000042 iter = 5 | cost = -24.472231940032042 iter = 6 | cost = -24.472231940032042 iter = 7 | cost = -24.472231940032042 iter = 8 | cost = -24.50816706605304 iter = 9 | cost = -24.50816706605304 経過時間:3.0799999237060547
plt.plot(hist_cost,'o-')
この例では、所要時間はあまり変わりません。
しかしQAOAのレイヤー数、つまりパラメータの数を増やすと劇的に違います。
例えばレイヤー数を10、scipy.minimizeのmethodをmethod='Powell'とした場合では、
非勾配は数分かかりますが勾配法は30秒程度で終了します。
パラメータ数が数十、数百となってくると、勾配法のメリットが出てきます。